內含報酬率的求解及多解問題分析

冀聰慧

摘要：內含報酬率（IRR）作為投資項目評價的重要指標，應用比較廣泛。傳統求解IRR的方法計算復雜、精確度不高；而財務中常用的軟件Excel操作簡單、結果準確，但對于多解問題沒有比較普及的求解方法。文章分別介紹了常規項目和非常規項目的IRR在Excel中的求解方法，并在非常規項目IRR的多解問題上，從其經濟內涵出發提出了排除方法。

關鍵詞：內含報酬率 Excel 多解問題

中圖分類號：F234 文獻標識碼：A 文章編號：1002-5812（2016）15-0087-02

內含報酬率（IRR）是項目投資決策中一個重要的動態評價指標，將它與資金成本率比較，可以反映出該項目的可行性，相比于一些絕對量指標更能直觀地評價投資項目；另外，內含報酬率在不需要基準折現率的情況下就能求解出來，其值的大小不受外部參數的影響而完全取決于項目本身的現金流量，因此在財務領域被廣泛應用。眾所周知，內含報酬率是指投資項目的凈現值等于零時的貼現率，計算公式為：

其中：IRR為內含報酬率，CFt為第t年的現金流量，n為項目的存續期。對于單一的投資方案，若求得的內含報酬率高于企業的資金成本率，則可以接受該投資方案，否則，應該拒絕該投資方案；在進行多個互斥的投資方案決策時，應該選擇內含報酬率最大的投資方案。

一、傳統求解方法的缺陷

對于內含報酬率的求解，傳統方法為插值法，若要使計算結果貼近IRR的真值，必須使所取的插值區間盡可能地小，所以確定插值區間是插值法的關鍵。確定插值區間的一般做法是：當投資項目每年的現金流量相等時，采用“查表法”，計算出投資項目的年金現值系數，查年金現值系數表，找出對應的折現率區間即為插值區間；當每年的現金流量不相等時，采用“逐次測試法”，通過試誤，找到使凈現值出現一正一負的兩個值。

然而，傳統方法在應用過程中存在明顯的缺陷。其一，在確定插值區間時，“查表法”要求投資項目每年的現金流量相等，條件苛刻，這樣的投資項目在現實生活中幾乎不存在；若采用“逐次測試法”，計算復雜、手工計算量大，尤其當各期凈現金流的數量較多時，若第一次測試用的折現率遠離目標利率，還會增加測試工作量。其二，“插值法”本身準確度不高，它是一種“以直代曲，按比例計算”的方法，無法得出準確的值，由于凈現值曲線是與水平線漸近的曲線，確定直線的兩點分別在橫軸的兩側，所以用“插值法”計算出的內含報酬率的近似值大于內含報酬率的真實值，這種誤差如果不加以有效控制甚至可能影響決策的正確性，因此要提高內部收益率評價的效果和準確性，就要尋求新的計算方法。

二、Excel求解方法

鑒于傳統求解方法的不足，下面對在Excel中求解IRR進行舉例說明：

（一）常規項目的IRR求解。

例1：假設某公司將200萬元用于某項六年期的投資，第1—6年的凈現金流量分別為45萬元、50萬元、60萬元、70萬元、65萬元、55萬元。試計算此方案的內含報酬率。

1.IRR函數法。（1）選定一張Excel工作表，在A1—A7單元格依次輸入初始投資額及各年的現金流量，即： -200，45，50，60，70，65，50（注：初始投資額用負數表示）。（2）在單元格B1輸入“=IRR（A1∶A7）”，并“回車”，即可得到內含報酬率的值：16.81%。

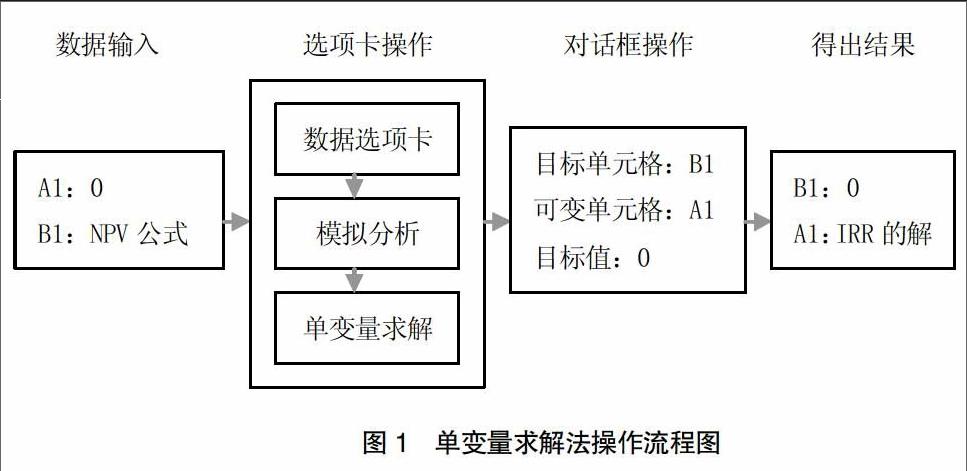
2.單變量求解法。（1）選定一張Excel工作表，在單元格A1輸入0，在單元格B1輸入凈現值NPV公式“=NPV（A1，45，50，60，70，65，50）-200”。（2）單擊“數據選項卡”→“模擬分析”→“單變量求解”，彈出“單變量求解”對話框。其中，“目標單元格”選擇“B1”，“可變單元格”選擇“A1”，目標值輸入0，點擊“確定”，顯示單變量求解狀態，當B1單元格值為0時，A1單元格的值16.81%就是解。操作過程如圖1所示。

例1是一個常規項目，常規項目是指投資發生在初期、以后各年發生連續的凈現金流入的項目。對于常規項目來說，IRR最多有一個解；而非常規項目的現金流符號變化兩次或兩次以上，根據笛卡爾關于高次方程的符號規則：系數為實數的高次多項式，其正實根的數目不會超過其系數序列符號的變更次數，當凈現金流量序列有兩次或者多次符號變化時，可能出現多個正值的內部收益率，這時按照前面的求解步驟不能求出所有的IRR值，下面對非常規項目的IRR求解原理進行分析并說明其步驟。

（二）非常規項目的IRR求解。

例2：某公司初始投資額為900萬元，第1—5年的凈現金流量分別為1 200萬元、987萬元、-1 600萬元、200萬元、100萬元。試計算該項目的內部收益率。

1.IRR函數法。若按前面常規項目的求解過程操作，得出的解為5.80%，但實際上該現金流序列存在兩個解：5.80%、17.01%。IRR函數之所以不能求出所有的解是因為它求出IRR的一個解后就返回結果停止工作，IRR函數的原型為IRR（Values，[Guess]），其中Guess是對IRR結果的估計值，默認值為0.01，Excel使用迭代法計算，從Guess=0.01開始，不斷修正計算結果，找到解后停止；如果IRR運算20次，仍未找到結果，則返回錯誤值#NUM！。在例2中若要找到另一個解就要改變Guess值，具體步驟為：在IRR函數中加入參數Guess，將其值從0.01開始逐漸遞加，當加到0.12時，IRR的值變為17.01%，此為IRR的第二個解。

2.單變量求解法。在單變量求解法中，具體步驟為：求出第一個解5.80%后，改變A1單元格的初始值為1，再執行單變量求解法的第二個步驟，求得IRR為17.01%。因為Excel中的單變量求解，只能得出一解，可以通過改變可變單元格的初始值找到另外的解，可變單元格的初始值在使內含報酬率的值有意義的區間：0—1范圍內改變。

三、內含報酬率多解問題分析

同時出現多個內含報酬率的投資方案，必定是非常規方案，但并不是每一個非常規方案都會同時出現多個內含報酬率。按照財務管理的理論，如果有一個方案出現了多個IRR而不能排除，則內含報酬率不再適用于該投資方案的評價，因此遇到這種情況時有效進行IRR的排除是投資決策中關鍵的程序。

（一）多解問題的排除原理。通過計算得出的IRR都符合其定義，但是它們并不一定符合內含報酬率的經濟內涵。在非常規項目中應用內含報酬率的公式計算時實際上隱含了再投資假設，再投資假設解決的是若存在再投資機會，公司利用較早獲得的現金流入量進行再投資，其投資報酬率至少是多少的問題。觀察內含報酬率的公式很容易看出它所假設的再投資報酬率為內含報酬率，這樣，內含報酬率法按照內含報酬率評估再投資機會，但實際上這種做法欠妥，非常規項目的凈現金流出現負值很可能是由分期投資或滾動投資造成的，此時合理的貼現率應該是資本成本。在常規項目中，只存在一個內含報酬率，除了初始投資的凈現金流為負，以后各年現金流符號都為正，投資是在整個投資年限末才收回的，因此不存在再投資假設。對例1來說，其投資回收期內現值累計變化計算如表1，在16.81%的內含報酬率下，初始投資在1—5年都存在未收回的金額，只有在項目投資期末才完全收回，不存在再投資問題。

筆者認為，要使非常規項目的內含報酬率能客觀評價該項目，就要去除內含報酬率計算過程中所隱含的不合理的再投資假設對結果的影響，使投資項目中不存在再投資收益率問題，在非常規項目存在多個內部收益率時根據下述規則進行排除：按合理的IRR計算，投資項目在整個壽命期內必須始終處于投資回收狀態，各年均存在未收回投資額。也就是說，使投資回收期內出現正的累計現值的內含報酬率應該被排除掉。當非常規投資項目有多個正實數根時，須經過檢驗，符合經濟涵義的根才是項目的內部收益率；如果只有一個正實數根，同樣需要檢驗。

（二）排除決策舉例。依然沿用例2，根據兩個內含報酬率：5.80%、17.01%計算出的投資回收期內各年累計現值變化如表2，可以看出投資項目并非始終處于未回收狀態，而是在第1年和第2年出現了局部盈余，現值累計為正值，與上述規則不符，所以5.80%和17.01%不符合投資項目內部收益率的經濟涵義，可以排除。

四、結論

對于常規項目，運用Excel中的IRR函數法或單變量求解法即可準確簡便地求出內含報酬率；對于非常規項目，仍可在兩種方法的基礎上稍作改動求出它的多個解：IRR函數法通過不斷修改Guess值求出多解，單變量求解法通過改變可變單元格的初始值求出多解。但是，用Excel求出的非常規項目的一個或多個IRR不一定符合內含報酬率的經濟內涵，應該去除不合理假設的再投資報酬率的影響，根據各年的現值累計有效地進行排除。

參考文獻：

[1]葉璋禮.基于年金特征的內部收益率速算研究[J].商業會計，2014，（08）：76-78.

[2]李萍.利用Excel函數功能計算凈現值和內含報酬率[J].當代會計，2014，（02）：38-40.

[3]劉姝蕙，陳錦輝.運用二分法求解內含報酬率[J].財會月刊，2012，（26）：52.

[4]馬良渝.求解IRR的多個解的Excel方法[J].中國管理信息化，2005，（10）：20.