經典控制理論在飛行控制系統中的設計應用

劉伯健

摘要：飛行控制系統對控制飛機起到了至關重要的作用。飛行控制系統可用來保證飛行器的穩定性和操縱性、提高完成任務的能力與飛行品質、增強飛行的安全及減輕駕駛員負擔。然而如何設計閉環飛行控制系統的反饋參數，使此系統能擁有良好的動態特性和飛機控制力。本文以F16飛機模型為例，以經典控制理論中的根軌跡法為切入點，運用MATLAB軟件進行仿真分析設計，最終設計閉環飛行控制系統的反饋參數。

Abstract： Flight control system has played a vital role in controlling the flight. Flight control system can be used to guarantee stability and maneuverability of aircraft， improve the ability of completing the task and flying qualities， enhance flight safety and reduce the burden of the pilot. However， how to design the closed-loop feedback parameters of flight control system can make the system has good dynamic characteristics and good ability of controlling the plane. This article takes F16 airplane model as an example. Based on the root locus method for classical control theory， the author finally designs a closed-loop feedback parameters of flight control system by using the MATLAB software simulation.

關鍵詞：經典控制理論；飛行控制系統；自動控制

Key words： classical control theory；flight control system；automatic control

中圖分類號：V249.1 文獻標識碼：A 文章編號：1006-4311（2016）09-0151-04

0 引言

飛行控制系統是對飛機姿態進行控制的系統，此系統動態性能的優良與否是控制飛機穩定飛行的關鍵所在。隨著飛行器的不斷進步，對飛行控制系統的要求也不斷提升，各國對飛行控制系統的改進研究也在不斷前進。文章從經典控制理論的根軌跡法出發，對飛行控制系統的反饋參數進行設計并運用MATLAB進行仿真驗證。

經典控制理論是建立在頻率響應法和根軌跡法基礎上。經典控制理論的研究對象是單輸入、單輸出的控制系統。經典控制理論的特點是以輸入輸出特性為系統數學模型，采用頻率響應法和根軌跡法等圖解分析方法，分析系統性能和設計控制裝置。雖然現在出現了現代控制理論，可是經典控制理論在自動控制系統的設計上，仍占有著不可替代的位置。下面我們就以經典控制理論設計F16飛機的控制反饋系統，并以MATLAB進行仿真驗證。

飛機可以分為兩個控制面，橫向控制面和縱向控制面，兩個控制面存在耦合和相互作用。但是本文此次設計僅針對于忽略橫縱向耦合并且線性化配平過后的開環F16飛機系統，力求得到一個比較完美的動態響應特性，使系統達到超調量小于百分之五，調節時間小于3s的良好動態特性，并盡量減小荷蘭滾模態的系數的閉環飛行控制系統。

由于飛機在不同飛行高度、飛行速度的配平參數不同（即狀態矩陣不同），所以本文僅就F16在3500m，150m/s的狀態配平下進行飛機橫向反饋系統設計（配平已知）。

飛機橫向反饋系統設計：

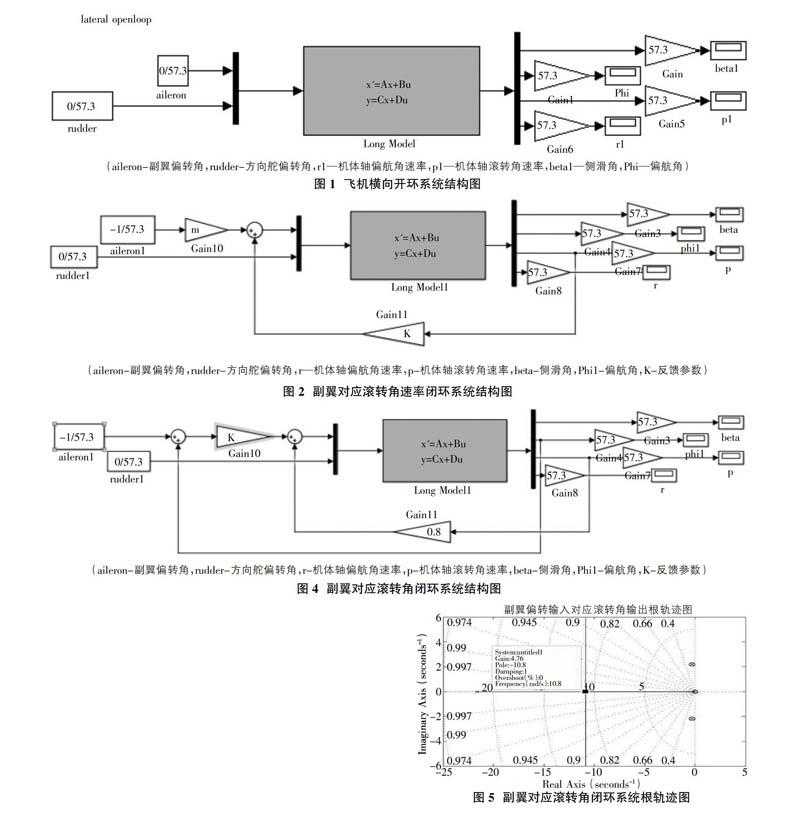
如圖1所示，對于飛機橫向系統來說，此系統是二輸入四輸出的系統。構建simlink結構圖，出于簡化問題的考慮，我們只研究副翼偏轉對應滾轉角系統和方向舵偏轉對應航向角系統的反饋線路設計。首先我們先研究副翼偏轉對應滾轉角系統的反饋設計。

1 副翼偏轉對應滾轉角系統的反饋設計

與方向舵—俯仰角系統一樣，我們需要先調節好副翼偏轉對應滾轉角速度系統的動態特性。方案如下：

①副翼偏轉對應滾轉角速度系統的反饋設計。

如圖2所示，運用Simulink中Gain環節構建反饋線路，圖中的K就是我們需要確定的反饋參數，因此我們需要得到副翼對應滾轉角速率系統的開環傳遞函數：

G=■

根據開環傳遞函數繪制出根軌跡圖（圖3）。

■

如圖3根軌跡圖可看出，傳遞函數共有四個極點：p1，p2對應荷蘭滾模態；p3對應滾轉模態；p4對應螺旋模態。隨著K值的增大，極點p3左移，滾轉角速率對應階躍響應的調節時間減小，系統動態特性更好；但當K>0.138時，隨著K的增大，荷蘭滾模態對應的阻尼比減小，荷蘭滾運動較劇烈，因此，在滿足一定動態性能要求時要使K盡量小。

經調試發現當K=0.8時，調節時間為0.108s，超調量為5%，系統動態特性較好，且K值較小，荷蘭滾運動尚可。不妨選取k=0.8。以此為基礎，進行副翼偏轉對應滾轉角系統的反饋設計。

2 副翼偏轉對應滾轉角系統的反饋設計

如圖4所示副翼對應滾轉角閉環系統結構圖中的K即是我們需要確定的反饋參數，內環即是上述內容設計出來的副翼偏轉對應滾轉角速度系統。首先我們得到副翼對應滾轉角閉環系統的開環傳遞函數：

G=■

根據開環傳遞函數繪制出系統根軌跡圖（圖5）。

從圖5中我們不難發現，這是一個3零點5極點的根軌跡圖，其中有三對零極點互相消去，剩下兩個極點對系統產生重要影響（即振蕩環節根軌跡）。我們不妨取K=4.75，由經典控制理論系統此時應有最好的動態特性。

當K=4.75時，系統超調量為1.12%，調節時間為0.49s，滾轉角對應副翼偏轉響應動態性能最好，同時滿足設計指標，荷蘭滾模態參數尚可。所以我們選取K=4.75。至此副翼對應滾轉角閉環系統反饋設計結束。

下面我們對橫向面第二個系統進行反饋設計。

3 方向舵對應偏航角系統反饋設計

3.1 方向舵對應偏航角速度系統

首先我們得到其開環系統傳遞函數：

G=■

通過開環傳遞函數，我們可以畫出根軌跡圖（圖7）。

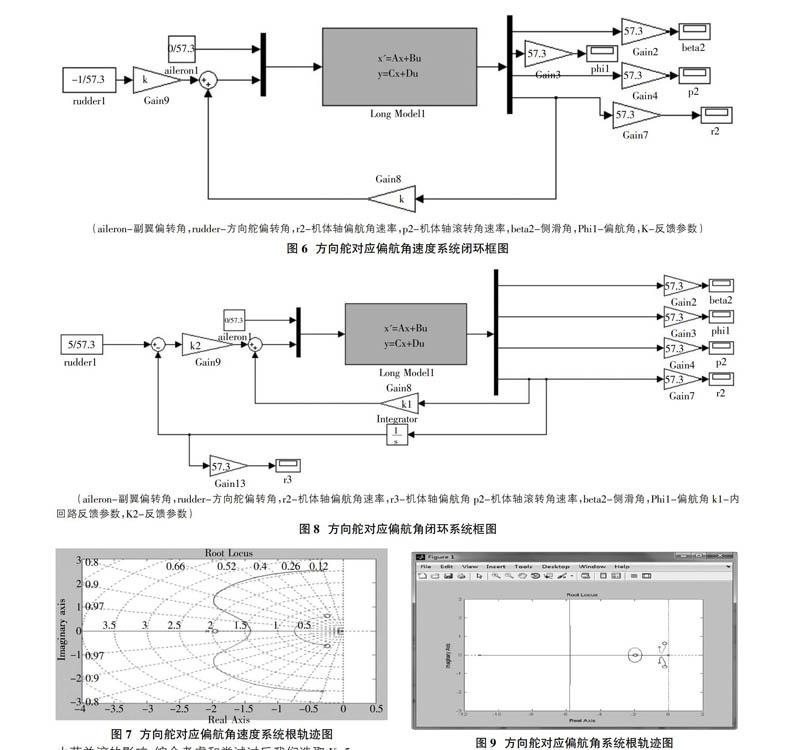
由圖7所示由于系統響應的主要根軌跡是實軸上的根軌跡，所以顯而易見系統的K值越大動態特性也就越好，但是由于需要減小荷蘭滾模態的影響，k應該在1.92到3.17左右。兩個參量相互影響，所以我們不妨設定個參數：超調量不得超過百分之五，調節時間不得超過3s，同時盡可能減小荷蘭滾的影響，綜合考慮和嘗試過后我們選取K=5。

3.2 方向舵對應偏航角系統

根據上述內容，在偏航角速度的測速反饋系統中，我們采取K1=5作為反饋系數，在此基礎上我們進行偏航角系統的反饋參數設計。

首先我們根據系統圖8推導出傳遞函數：

G=■

根據傳遞函數繪制出根軌跡圖：

從圖9中我們不難發現，這是一個3零點5極點的根軌跡圖，其中有三對零極點互相消去，剩下兩個極點對系統產生重要影響（即振蕩環節根軌跡）。K2較小時，根軌跡處于過阻尼狀態，調節時間較大；K2較大時，處于欠阻尼狀態，系統超調量會增大，所以我們不妨取K2=12.3（震蕩環節交點），系統理論應有最好的動態特性。

從上圖不難看出，當K2<12.3時，調節時間會增加，超調量小。當k2>12.3時，調節時間縮小，但是會有大超調量產生。所以我們選取K2=12.3作為我們的方向舵對應偏航角系統的反饋參數時，滿足設計指標。至此方向舵對應偏航角系統反饋設計結束。此時飛機控制系統在互不影響的前提下，運用如上反饋網絡，系統的動態特性滿足超調量不大于5%，調節時間不大于3S的指標。

4 結語

以上方法，是運用根軌跡法，對飛行橫向控制面反饋系統進行參數設計。根軌跡法作為經典控制理論重要的一部分，在飛行控制上的應用遠不止如此。在現代控制理論飛速發展的今天，經典控制理論以其獨特的魅力，仍在飛行控制方面發揮著不可忽視的作用。

參考文獻：

[1]鄭超.基于MATLAB的根軌跡法的研究[J].山西師范大學學報（自然科學版），2008，S2：29-34.

[2]盧京潮，趙忠，劉慧英，袁冬莉，賈秋玲.自動控制原理[M]. 北京清華大學出版社，2008.

[3]賈秋玲，袁冬莉，欒云鳳.基于MATLAB7.X/Simulink/Stateflow系統仿真.分析及設計[M].西安西北工業大學出版社，2006.