永磁同步電機的無差拍預測轉矩控制系統*

浦龍梅，　張宏立

(1. 新疆建設職業技術學院，新疆 烏魯木齊　830000；2. 新疆大學 電氣工程學院，新疆 烏魯木齊　830000)

?

永磁同步電機的無差拍預測轉矩控制系統*

浦龍梅1，張宏立2

(1. 新疆建設職業技術學院，新疆 烏魯木齊830000；2. 新疆大學 電氣工程學院，新疆 烏魯木齊830000)

將無差拍控制理論應用于永磁同步電機預測轉矩控制系統，通過求解無差拍期望電壓矢量，判斷其空間位置，縮小逆變器輸出電壓矢量的優選范圍。應用無差拍預測轉矩控制策略，單步預測滾動優化次數由傳統預測轉矩控制的7次降低至3次，多步預測節省系統運算資源的效果更優。仿真和試驗結果表明無差拍預測轉矩控制策略在繼承預測轉矩控制優越動、穩態性能的同時還能減輕系統的運算負擔。

無差拍控制； 預測轉矩控制； 運算負擔； 滾動優化

0　引　言

有限控制集模型預測控制(Finite Control Set Model Predictive Control, FCS-MPC)自提出以來[1]，得到了諸多學者的廣泛關注。預測轉矩控制(Predictive Torque Control, PTC)在保持傳統直接轉矩控制高動態性能的同時，在處理非線性約束問題時具有更優的靈活性[2]。但是，轉矩預測在線尋優算法運算量巨大[3]，尤其應用于多步預測控制或者多電平、不對稱拓撲結構時，對控制系統硬件支撐提出了一定的挑戰。在同一應用平臺，巨大運算量勢必帶來采樣周期長、開關頻率低等問題，從而導致電機轉矩脈動大、定子電流質量低。

針對上述問題，有學者提出離線優化方法[4]，以減輕在線尋優的運算負擔。但離線策略存在時效性差及數據片面性等問題，無法直觀體現模型預測控制在線滾動優化的優勢。另有學者指出可結合調制策略以消除轉矩紋波[5]，雖效果突出但運算負擔并未得到緩解，反而增加了控制系統的復雜程度。

本文針對永磁同步電機PTC系統，結合無差拍(Dead Beat, DB)控制理論[6-7]，研究了一種適用于永磁同步電機的無差拍預測轉矩控制(Dead Beat Predictive Torque Control, DB-PTC)策略。通過無差拍控制器，所有電壓矢量不再逐一參與價值函數的評估，從而縮小了最優電壓矢量的篩選范圍，減少了在線優化的滾動次數。在降低控制系統運算量的同時，還能獲得與PTC相似的控制效果。

1　永磁同步電機PTC

永磁同步電機在轉子兩相同步旋轉坐標系下的連續時域模型為

(1)

(2)

其中：

ψd=Ldid+ψf，ψq=Lqiq

式中：ud、uq，id、iq，ψd、ψq——d-q坐標系下的定子電壓、電流和磁鏈；

Rs——定子電阻；

Ld、Lq——定子d、q軸等效電感；

ωe——轉子電氣角速度；

Te——電機電磁轉矩；

p——轉子極對數；

ψf——轉子永磁體磁鏈。

PTC利用功率變換器的離散化本質，通過滾動優化，直接選出使單一價值函數最小的最優電壓矢量。因而，利用前向歐拉法可得到k+1時刻的轉矩和磁鏈預測值為

(3)

式中：Ts——采樣周期；

k——時刻。

若忽略定子電阻，則k+1時刻的定子磁鏈幅值為

(4)

模型預測控制中價值函數反映系統控制指標，在兩電平逆變器驅動的永磁同步電機PTC系統中，除轉矩和磁鏈兩個主控目標外，還要對系統開關頻率進行限制，同時還要設置過流保護等，即有

(5)

其中：

(6)

式中：n——預測步數；

Tek+n、ψsk+n——k+n時刻的轉矩和磁鏈預測值；

Q1、Q2——權值系數，表示轉矩跟蹤和磁鏈跟蹤兩個控制目標的相對重要性；

j=1,2,…,7——兩電平逆變器可產生的7個開關狀態；

Imax——逆變器可輸出的最大電流，表示電機在正常工作時其相電流不應大于該閾值。

因此，根據式(5)選出的最優電壓矢量均能夠保障系統的穩定運行。永磁同步電機PTC結構如圖1所示。

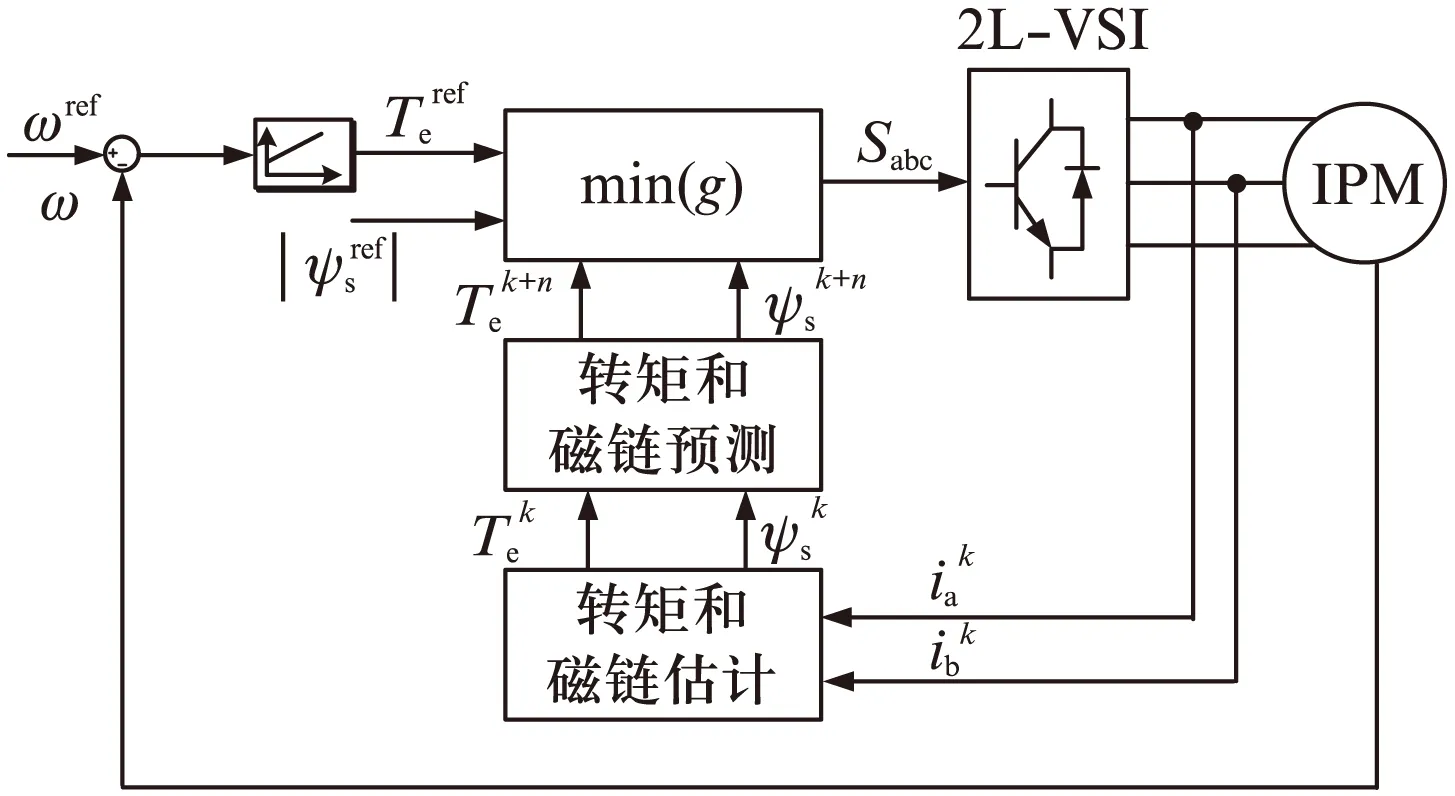
圖1　永磁同步電機PTC結構

相較于傳統直接轉矩控制策略，FCS-PTC的優越性在于對逆變器產生的所有電壓矢量進行逐一優選。但是，當逆變器可輸出電壓矢量較多且采樣頻率較高時，巨大運算量使開關控制信號延遲，從而導致系統性能惡化。圖2為傳統PTC預測時域過程，預測步數較大(N>1)時，一個采樣周期內無法完成對下一時刻預測值的計算。

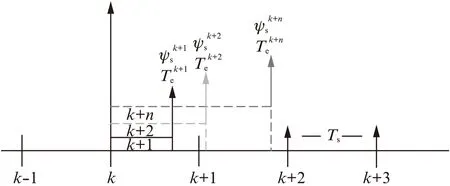
圖2　傳統PTC預測時域過程

2　永磁同步電機DB-PTC

2.1無差拍電壓矢量優選

無差拍控制建立在系統離散模型之上，在一個控制周期內使被控量達到其期望值。在永磁同步電機控制系統中，以電磁轉矩和定子磁鏈幅值的零跟蹤誤差為控制目標，直接計算出加在定子端的最優電壓矢量。

對式(2)求導并離散化可得到用于無差拍控制的系統方程：

(7)

其中：

根據無差拍控制的定義，令Tek+1=Teref，ψsk+1=ψsref；聯立式(4)、式(7)可計算得到無差拍控制期望電壓矢量udk、uqk。

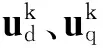
首先，利用Park變換得到定子靜止坐標系下的無差拍期望電壓矢量：

(8)

則無差拍期望電壓矢量所在扇區位置為

通過判斷θDB大小即可確定DB-PTC的最優電壓矢量選擇范圍，如圖3所示。最優電壓矢量的選擇范圍由傳統PTC的7個電壓矢量縮小至3個電壓矢量，分別為相鄰兩個有效矢量和一個零矢量。表1為不同扇區傳統PTC和DB-PTC對應的最優電壓矢量選擇范圍。

θDB[0,π/3](π/3,2π/3](2π/3,π](π,4π/3](4π/3,5π/3](5π/3,π]SDB123456PTC可選電壓矢量000,…,111000,…,111000,…,111000,…,111000,…,111000,…,111DB-PTC可選電壓矢量000,100,110000,110,010000,010,011000,011,001000,001,101000,101,100

2.2系統控制結構

對于傳統的PTC策略，每一步預測其滾動優化次數始終為7。這種以指數形式增長的計算量勢必會加重系統的運算負擔。相比之下，DB-PTC每步預測僅滾動3次，預測步數越大，其節省運算資源的效果愈加明顯。兩種控制策略下多步預測電壓矢量的優選過程如圖4所示。

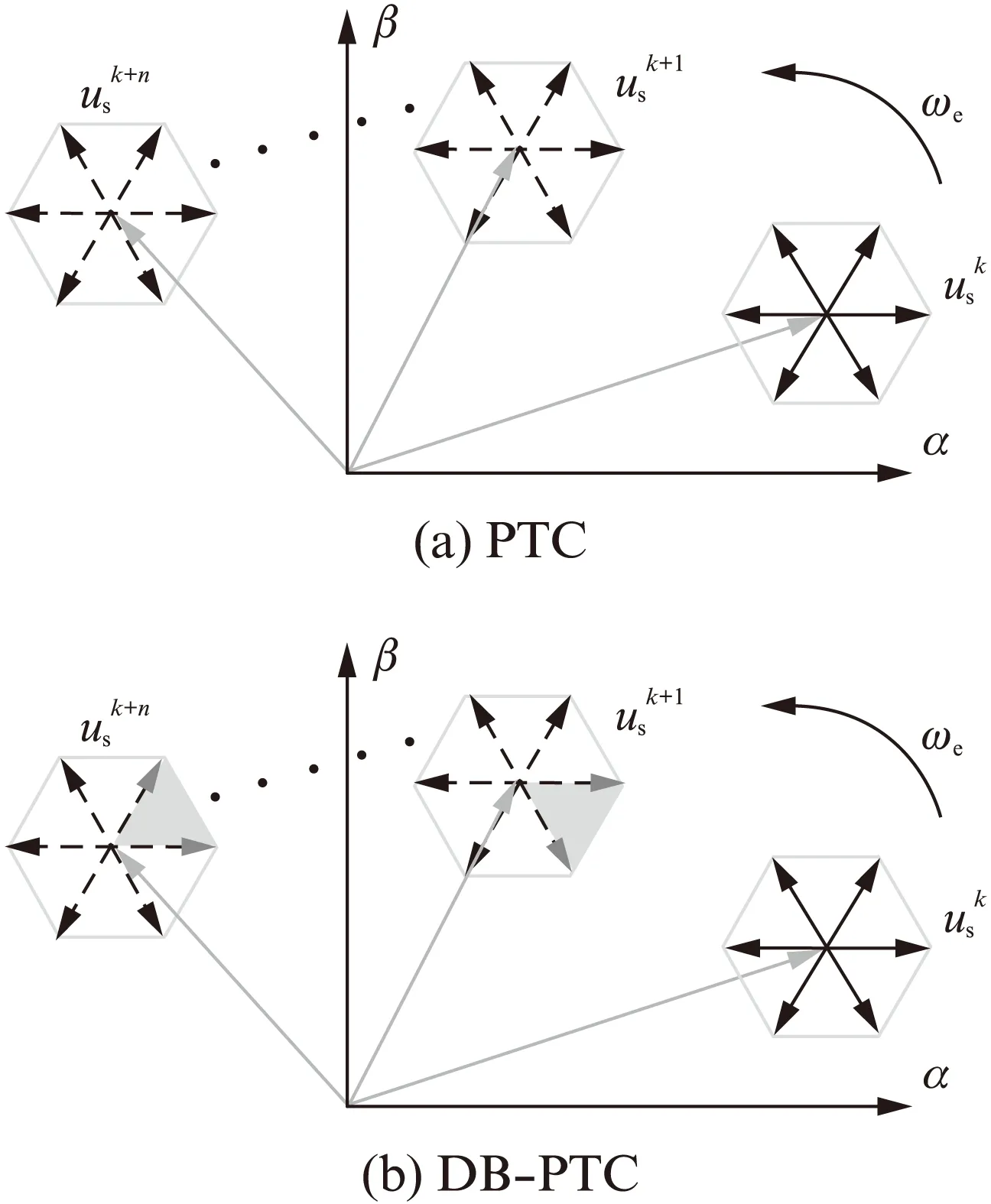
圖4　最優電壓矢量的選擇范圍

圖5為永磁同步電機DB-PTC結構，與傳統PTC結構相比，其增加了無差拍期望電壓矢量估測環節和電壓矢量優選范圍確定環節。

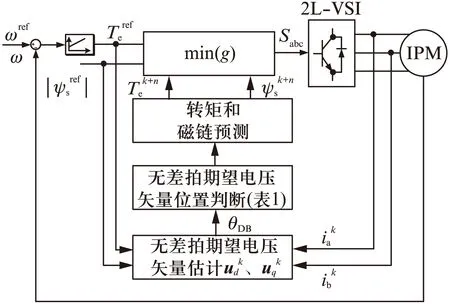
圖5　永磁同步電機DB-PTC結構

圖6為DB-PTC算法流程圖，其中預測步數N=1。由表1可知，在每一扇區對應的可選電壓

矢量中總有零矢量的存在。為避免零矢量的漏選，構建了新的電壓序列，即[001,000,010,000,011,…,000,001]。即當開關狀態i=1時，對應電壓矢量001；當i=2時，對應電壓矢量000；當i=3時，對應電壓矢量010；當i=4時，對應電壓矢量000；當i=12時，對應電壓矢量000；當i=13時，對應電壓矢量001。可以發現，零矢量對應的開關狀態均為偶數。同時，對于每一扇區SDB，僅滾動計算3次。

3　仿真分析及試驗研究

3.1仿真分析

搭建了基于MATLAB/Simulink的仿真試驗平臺，對DB-PTC和傳統PTC方法進行了仿真對比分析。其中電機參數如下： 定子電阻1.25Ω，d軸電感12mH，q軸電感30mH，轉子磁鏈0.45Wb，極對數為5，額定轉速1000r/min。

永磁同步電機DB-PTC系統在不同速度段運行時的響應波形如圖7所示。電機初始為靜止狀態，在0.52s起動后加速運行至額定速度。在該過程中，電機輸出額定轉矩以便擁有盡可能高的加速度。電機轉速達到給定值后經短暫的超調過程進入穩定運行階段。在2.05s時，給定轉速由1000r/min突變至-1000r/min，電機逐漸由正轉狀態過渡至反轉運行。由圖7可以看出，在整個運行階段，電機轉速和電磁轉矩均表現出良好的跟蹤性能，同時定子電流質量很高。

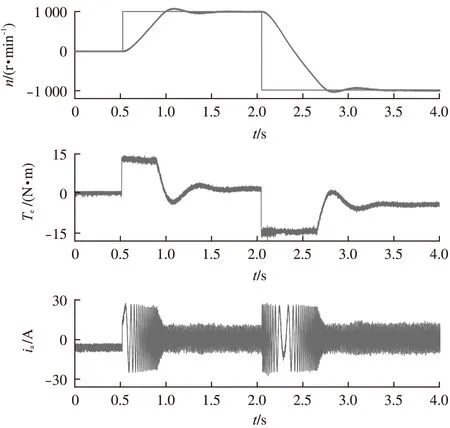
圖7　DB-PTC全速域運行結果

圖8為電機起動過程傳統PTC和DB-PTC兩種方法下的開關狀態變化對比。由圖8可以看出，在轉矩階躍變化過程中，兩者動態響應時間都很短，說明DB-PTC繼承了PTC優越的動態性能。另外，在暫態響應過程中，兩者輸出的最優電壓矢量均為有效電壓矢量，故可保證電機轉矩能夠以最快速度跟蹤參考值。

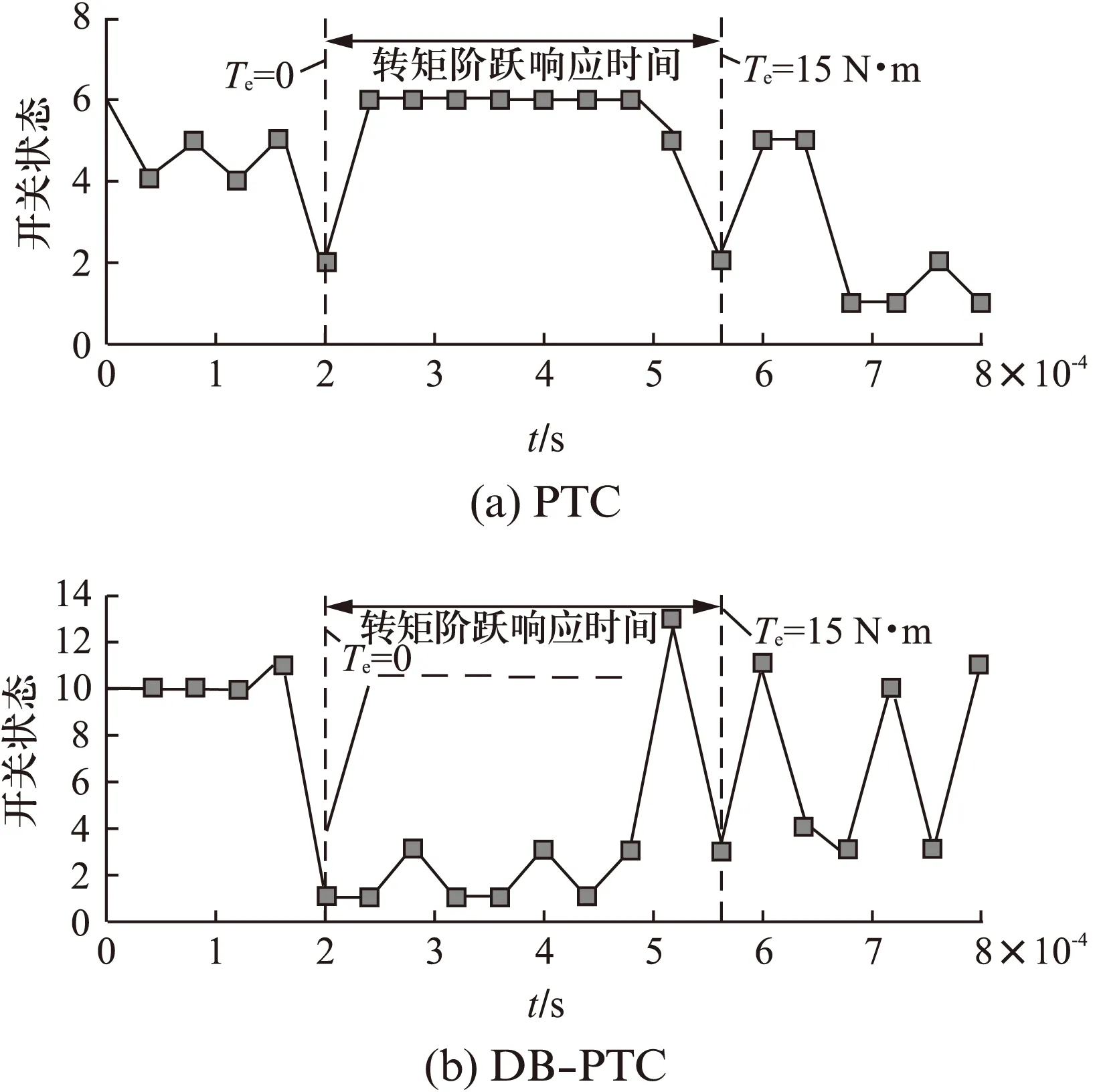
圖8　動態性能對比

3.2試驗研究

為驗證所提方法的性能，搭建了一臺內置永磁同步電機試驗樣機。其軸端與一臺直流電機相連，作為負載，電機參數同上。試驗平臺以TI公司的DSP TMS320F2812為控制核心，控制頻率為10kHz。為采用背靠背控制結構，整流模塊以二極管為開關器件，逆變模塊采用英飛凌公司的BSM10GB170-DLC型IGBT。采用增量式光電脈沖編碼器，其分辨率為2048脈沖/r。

圖9所示為PTC和DB-PTC兩種控制策略下預測算法耗時對比，算法計算時間由DSP的I/O口輸出高低電平至示波器測量得到。由圖9可以看出，單步預測(N=1)時，PTC滾動計算7次，DB-PTC滾動計算3次，兩種控制策略運算耗時接近，均在一個采樣周期之內。當預測步數較大(N=2)時，PTC滾動計算49次，而DB-PTC僅滾動計算9次，DB-PTC運算耗時遠低于PTC，說明所研究的DB-PTC策略在降低系統運算負擔方面有突出效果。

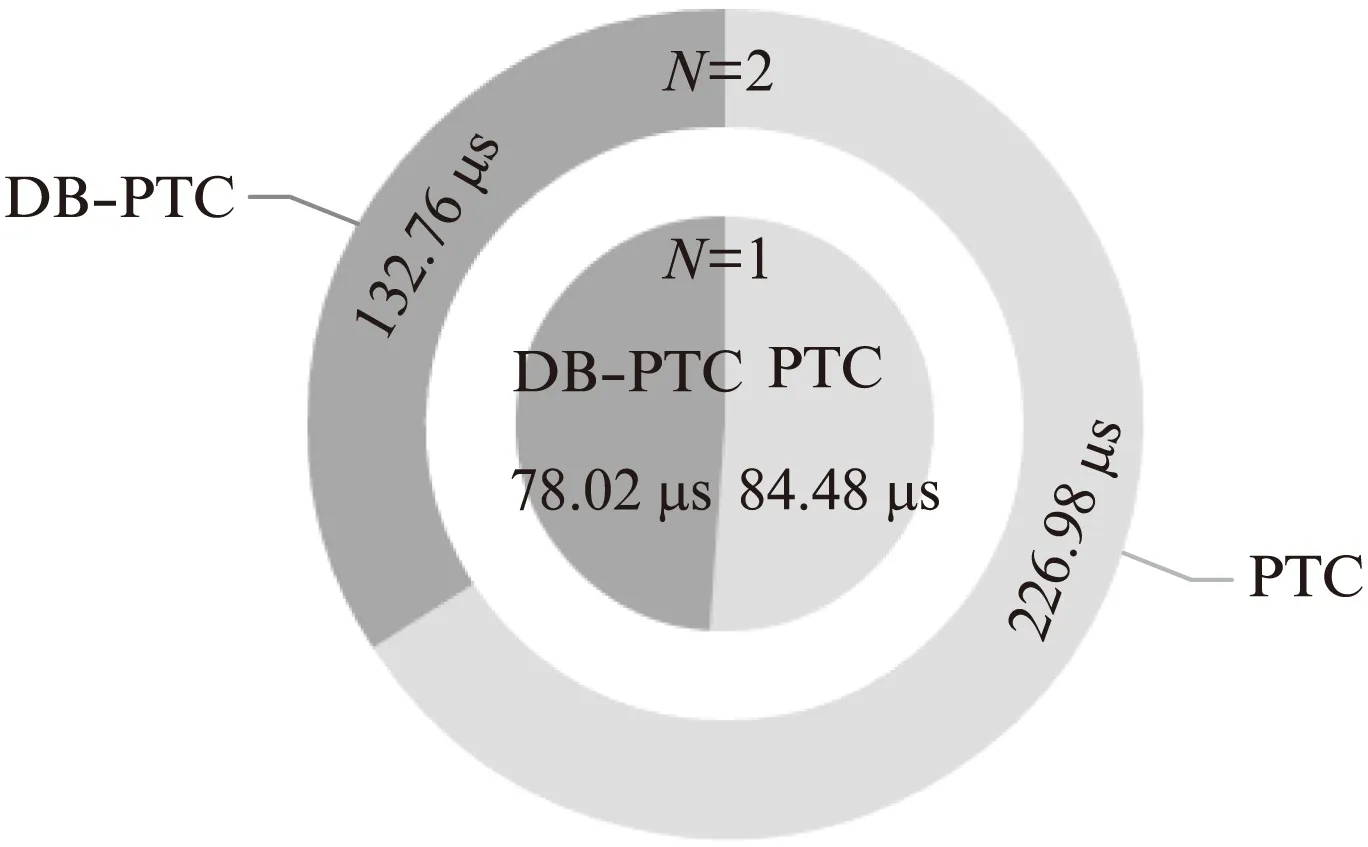
圖9　兩種控制策略算法耗時對比

圖10為電機穩態運行時的轉矩和a相電流波形，圖11為負載擾動下的定子電流和轉矩波形。從其試驗結果可以看出，DB-PTC方法具有與傳統PTC方法類似的動、穩態性能，表明了所提方法的有效性和可行性。

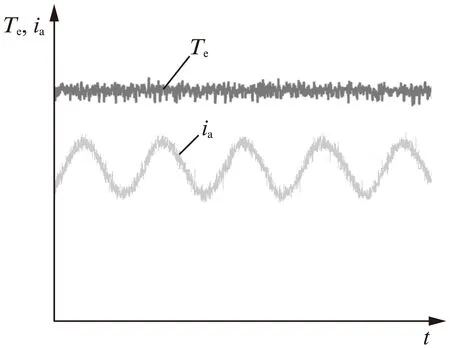
圖10　穩態試驗結果

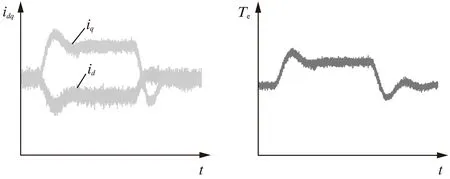
圖11　負載擾動試驗結果

4　結　語

本文研究表明，DB-PTC策略能夠明顯降低傳統PTC策略在線滾動優化運算量。通過判斷無差拍期望電壓矢量所在空間位置，縮小了逆變器輸出最優電壓矢量的篩選范圍，從而減輕了系統的計算負擔。試驗結果驗證了所提方法的有效性，同時所提方法具有與傳統PTC類似的動、穩態性能，因此在某些應用場合可將其取而代之。

[2]王晶鑫,姜建國.基于預測算法和變結構的矩陣變換器驅動感應電機無差拍直接轉矩控制[J].中國電機工程學報,2010，30(33)： 65-70.

[3]席裕庚,李德偉,林姝.模型預測控制——現狀與挑戰[J].自動化學報,2013,39(3)： 222-236.

[4]STOLZE P, TOMLINSON M, KENNEL R, et al. Heuristic finite-set model predictive current control for induction machines [C]∥2013 IEEE ECCE Asia Down Under, Crown Conference Centre, Melbourne, Australia, 2013： 1221-1226.

[5]ZHU H, XIAO X, LI Y. Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors[J]. Industrial Electronics IEEE Transactions on, 2012,59(2)： 871-877.

[6]王斌,王躍,王兆安.無速度傳感器的永磁同步電機無差拍直接轉矩控制方法[J].電機與控制學報,2014，18(6)： 42- 49.

[7]孫丹,陳殷,林斌.基于集成觀測器的PMSM無差拍直接轉矩控制系統[J].浙江大學學報(工學版),2015(6)： 1079-1086.

Predictive Torque Control with Dead Beat Solution for Permanent Magnet Synchronous Motor*

PULongmei1，ZHANGHongli2

(1. Xinjiang Vocational and Technical College of Construction, Urumqi 830000, China；2. College of Electrical Engineering, Xinjiang University, Urumqi 830000, China)

A control strategy of finite control set model predictive torque control with a deadbeat solution for permanent synchronous magnet motor drives was presented. By solving the desired voltage vector of deadbeat control and identifying which sector it was located, so the optimal range of output voltage vector was narrowed. For one step prediction based on a two-level inverter, the frequency of receding horizon optimization was reduced from seven to three compared with traditional predictive torque control strategy. For long steps prediction, the effect of cutting down computation burden was more significative .The Simulink and experimental results showed that the proposed strategy had a excellent dynamic and steady state performance similar with predictive torque control strategy. Moreover, the amount of computation was reduced.

dead beat control; predictive torque control; computation burden; receding horizon optimization

國家自然科學基金項目(51575469)

浦龍梅(1973—)，女，碩士，講師，研究方向為電氣自動化。

張宏立(1973—)，男，博士，副教授，研究生導師，研究方向為智能控制、機器學習等。

TM 351

A

1673-6540(2016)08- 0021- 05

2016-03-02