不完整信息下城市交通速度修復算法

鐘會玲，吳昊旻，陳迎迎，孫萬菊

（浙江浙大中控信息技術有限公司，浙江杭州 310053）

不完整信息下城市交通速度修復算法

鐘會玲，吳昊旻，陳迎迎，孫萬菊

（浙江浙大中控信息技術有限公司，浙江杭州 310053）

通過深入分析不完整信息數據的交通流路段速度，提出神經網絡與線性回歸組合模型的速度修復算法，利用相關性分析在交通流數據中找到路段速度在時間和空間上影響因素，將在時間上影響路段速度的因素作為神經網絡模型的輸入變量，將在空間上影響路段速度的因素作為神經網絡模型的輸入變量，分別輸出路段速度預測結果，將以上模型預測結果作為線性回歸模型輸入變量，最終得出路段速度二次預測結果。

交通流；路段速度；線性回歸；神經網絡；線性相關

將時間和空間組合的相關性引入交通數據分析可以較好地解決單純依賴時間序列和空間分析存在的問題，因此，本文引入時空組合模型對路段速度進行修復的方法，解決不完整信息下城市交通速度修復問題。

1 方法與數據

1.1方法

（1）BP神經網絡模型

神經網絡的訓練過程是一個不斷向樣本學習的過程，學習的目的是通過不斷調整網絡權值得到較小的預測誤差，BP神經網絡模型是一種以反向傳播算法學習的前饋式多層感知機，采用參數優化方法實現網絡權值的調整，參數優化是在一個特定模型結構M中，利用數據D優化模型參數，以求得使損失函數L（W）=L（W│D，M）達到最小時的模型參數W。損失函數L（W）的優化是以迭代方式體現，其特點是采用梯度下降法，每個時刻都本著使損失函數減小最快的原則調整網絡權值，不同類型問題的損失函數形式是不同的，一般預測問題的損失函數主要取決于預測模型和實際數據的誤差函數。

（2）線性回歸模型

回歸分析是研究隨機變量之間的相關關系的一種統計方法，其用意是研究一個被解釋變量（又稱因變量）與一個或多個解釋變量（又稱自變量）之間的統計關系。

論文利用的模型為多元線性回歸，將所選變量全部強行進入回歸，其線性模型即

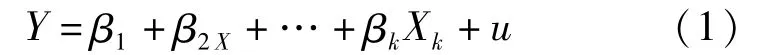
（3）相關分析

相關分析是研究兩數值型變量線性相關性的常用方法，需經過以下兩個步驟：第一，計算Pearson樣本相關系數r；第二，對樣本來自的兩總體是否存在顯著線性關系進行檢驗。

Pearson樣本相關系數即樣本簡單相關系數，反映變量間線性相關程度的強弱；對樣本來自的兩總體是否存在顯著線性關系進行檢驗，首先假設兩總體零線性相關，其次計算Pearson相關系數的檢驗統計量t及其對應的概率P，最后比較P與顯著性水平通常設為0.05得出是否線性相關結果。

論文通過運用相關性分析在交通流數據中找到路段速度在時間和空間上影響因素，利用神經網絡模型輸出路段速度預測和線性相關性結果，利用線性回歸模型得出路段速度二次預測結果，并利用測試集驗證結果，得出較高的線性相關度，表明該模型方法適用于城市交通速度修復。

1.2數據

為了驗證所提方法的有效性，以2015年浙江省紹興市交通流數據為研究對象，研究區域范圍現安裝有73個路口電子警察設備，可形成路段數為223，其中141個路段有數據，該電警數據包括車輛信息，車輛經過地點、方向，車道號及經過時間，利用該每5分鐘數據形成車輛經過某路段數據，并通過刪除滯留車輛數據，繞彎車輛數據達到清洗數據的目的，最后得出每5分鐘路段速度，論文選取以萬商路上笛揚路到金柯橋大道路段為研究對象，其中采用2015年3月至8月半年交通流數據處理完成后作為歷史數據，訓練集和測試集采用2015年9月至11月三個月交通流數據，分析時間上模型采用連續5分鐘同一路段速度數據，分析空間上模型采用同一時間段不同路段，其中不同路段數據由于設備老化或者由于未安裝只能采取部分不完整路段速度數據。

1.3實驗流程

原始交通流數據經過處理后形成路段過車數據，清洗干凈后計算出路段速度，然后通過混合模型分析數據，具體實驗流程如圖1所示，包括5個步驟：

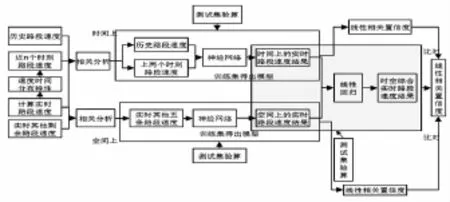
圖1　不完整信息下城市交通速度修復算法實驗流程

步驟一：原始交通流數據經過處理后形成路段過車數據，清洗干凈后計算出路段速度，同時通過繪圖得出速度的時間分布特性。

步驟二：利用相關分析分別得出路段速度在時間上和空間上的影響因素。

步驟三：利用BP神經網絡算法分別得出路段速度在時間和空間上與其影響因素間關系。

步驟四：利用測試集分別驗算時間和空間上計算得出的實時路段速度結果的準確率，同時利用線性回歸得出時間和空間上的路段速度結果與實際實時路段速度間線性關系結果。

步驟五：利用測試集驗算混合模型得出的實時路段速度結果的準確率，最后對比三種準確率。

2 結 果

2.1數據清洗結果與速度時間分布特性結果

論文以2015年9月至11月萬商路上的笛揚路到金柯橋大道的數據為研究對象，分析期間一周數據清洗前和清洗后數據量變化，該研究路段某一周內流量有28 702輛（已化為小車當量數），清洗后加入路段速度計算的數據有14 439行，有效數據占比81.3％，平均到每天每5分鐘實時有效數據偏低，必然會出現缺失數據，此處研究對象整體缺失率為45.54％，其中包括晚上數據缺失，白天數據缺失率為19.37％。

同時分析歷史交通路段速度在連續一周內的時間分布特性。交通路段速度的時間分布特性如圖2所示，由圖2可以看出，在7：00-9：00和17：00-19：00的時段內萬商路某一路段交通路段速度相對較低，呈現出早晚高峰的特征，且在連續的幾個工作日內路段速度變化大體相似，即在時間維度上具有相似性。

2.2時空相關分析結果

利用路段速度時間上的交通特性，在時間上，利用兩數值型變量線性相關模型，將歷史速度以及該時刻之前之后最近5個時刻速度輸入，得到上兩個時刻與歷史速度與當前時刻速度最為強相關。

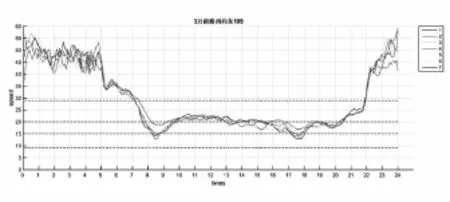
圖2　交通路段速度的時間分布

在空間上，利用兩數值型變量線性相關模型，將該路段速度和對應其他路段速度輸入，得到該路段速度與其他相鄰或相交的5條路段速度最為強相關，如圖4，其中93speed-3為目標路段變量，其他代表輸入路段自變量。其中紅色為目標路段，綠色為相關路段。

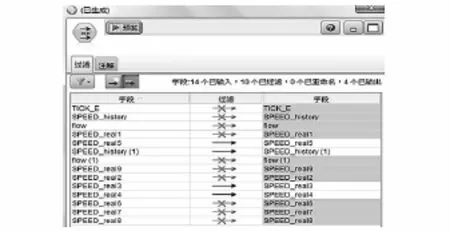
圖3　時間上速度強相關結果

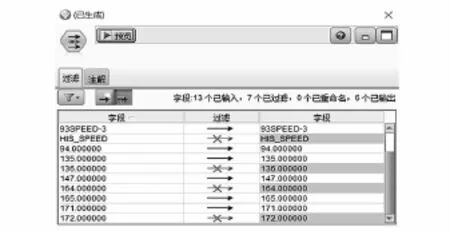
圖4　空間上速度強相關結果

2.3時空BP神經網絡算法結果

在上一步得出的時空相關分析結果基礎上，利用BP神經網絡算法利用訓練集分別得出在時間上歷史路段速度、上一個時刻路段速度與當時當刻路段速度關系，訓練集線性相關可信度為87.9％；在空間上目標路段速度與該區域對應時刻其他路段關系，訓練集線性相關可信度為86.6％。

利用測試集分別驗證時空關系結果，得出時間上利用BP神經網絡算法得出的線性相關可信度為90.4％，且預測值的平均絕對誤差為3.22 km/h；空間上利用BP神經網絡算法得出的線性相關可信度為88.1％，且預測值的平均絕對誤差為2.99km/h，時間上神經網絡預測值與實際值對比結果如圖5，空間上神經網絡預測值與實際值對比結果如圖6。

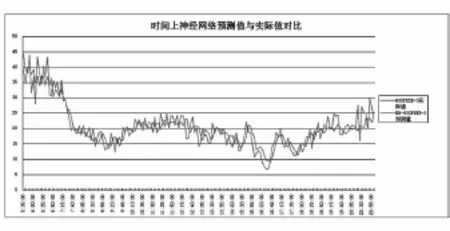
圖5　時間上神經網絡預測值與實際值對比結果

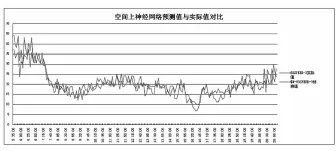
圖6　空間上神經網絡預測值與實際值對比結果

2.4時空線性回歸結果

在上一步得出的時空BP神經網絡算法結果基礎上，將訓練集利用線性回歸得出時間上關系結果、空間上關系結果兩種結果與路段速度關系。

利用測試集驗證回歸模型結果，得出利用BP神經網絡算法與線性回歸混合模型得出的訓練集線性相關可信度為89.4％，測試集線性相關可信度為91.7％，且預測值的平均絕對誤差為2.70 km/h；相比單獨從空間和時間上BP神經網絡模型，得出的路段行程速度的平均絕對誤差降低0.3～0.5 km ·h-1，混合模型預測值與實際值對比結果如圖7，采用組合模型進行速度插補如圖8。

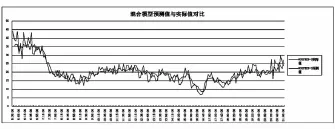
圖7　混合模型預測值與實際值對比結果

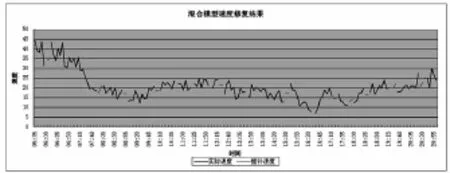
圖8　混合模型速度修復結果

3 討 論

首先論文為找到路段速度的影響因素，分別在時間和空間上對影響因素與路段速度進行相關性分析，從而得到在時間上上兩個時刻與歷史速度與當前時刻速度最為強相關，在空間上得到該路段速度與其他五條路段速度最為強相關。

其次論文在模型選取上，在時間和空間建模得出的結果下，再利用線性回歸模型，將時間和空間所得模型作為輸入變量，重新與路段速度得出新的線性關系，并且該組合模型得出的結果相比單獨神經網絡模型準確率偏高，說明模型選擇合理。

最后從研究結果看，空間上與目標路段速度相關的路段，基本上是相鄰、對面逆向路段或者與該路段相交的路段，說明上下游的交通流之間有相互影響，且影響較為明顯，時間和空間上路段速度與歷史速度以及上兩個時刻以及其他相鄰或相交路段相關，在當時當刻速度缺失的情況下可選擇利用組合模型預測出來的值進行插補。

4 結 論

論文通過有效分析得出，在時間上路段實時速度與對應歷史速度以及實時的上一時刻速度具有強線性相關，在空間上路段速度與相鄰路段和其他具有相同特性的路段具有強線性相關，并利用測試集驗證，最后空間和時間上的影響因素組合成新的線性模型得出結果，再次利用測試集驗證，其實驗數據證明，將空間和時間上的影響因素組合成新的線性模型得出結果較單獨模型得出速度結果具有更高的準確率，提高交通預測的準確性。

論文研究路段速度在空間上同一時間具有強線性相關的路段，可以作為目標路段速度缺失修復的方法，同時也可以研究路段速度在空間上不同時間具有強線性相關的路段，論文研究結果僅對時間跨度較小的缺失數據有效。不過論文研究結果可以完善交通數據庫，提高交通預測的準確性，同時一定程度上輔助管理部門了解實時城市交通運行情況，從而對經常擁堵路段采取應對措施。

如果想要修復時間跨度較大的路段速度數據可以通過以下方法，當預測目標路段在下一時段的速度及運行擁堵情況時，可以根據上一時刻與之相關的路段速度或者流量預測出來，該方法有待進一步研究，預期研究結果可以輔助管理部門為將來可能導致的嚴重擁堵路段提前做好準備與部署工作。

［1］ 蔣銳，王均.道路交通流數據檢驗與修復方法［J］.交通與計算機，2006，24（6）：65-67.

［2］ 瑞斯.瓊.數理統計與數據分析.田金方，譯［M］.北京：機械工業出版社，2009：340-341.

［3］ 陳封能，斯坦巴克.數據挖掘導論［M］.范明，譯.北京：人民郵電出版社，2011：222-223.

U492

C

1008-3383（2016）09-0166-03

2016-03-15

鐘會玲（1989-），女，碩士，研究方向：交通運輸。