活動導引，促進學生深度理解

李進衛

【設計理念】

正比例是刻畫某一現實背景中兩種相關聯的量變化規律的數學模型，是學生進一步學習一次函數的重要基礎。正比例的教學需要關注學生的原有知識基礎，了解學生對正比例意義的認識程度。通過學情調查，我發現：首先，學生對常用數量關系的理解比較清楚，給出兩種相關聯的量，他們能夠寫出數量關系式；其次，學生不清楚如何從變量的角度來認識兩者之間的關系，也不知道正比例的知識在日常生活、生產中的應用情況。

明晰了學生對這一教學內容的認識程度后，從學生的認知規律出發設計教學是達到良好教學效果的最佳路徑。本節課，我不斷地讓學生開展自主學習，經歷知識的形成過程，在比較討論中進行觀察，并歸納出正比例的意義。

1.理解兩種相關聯的量。

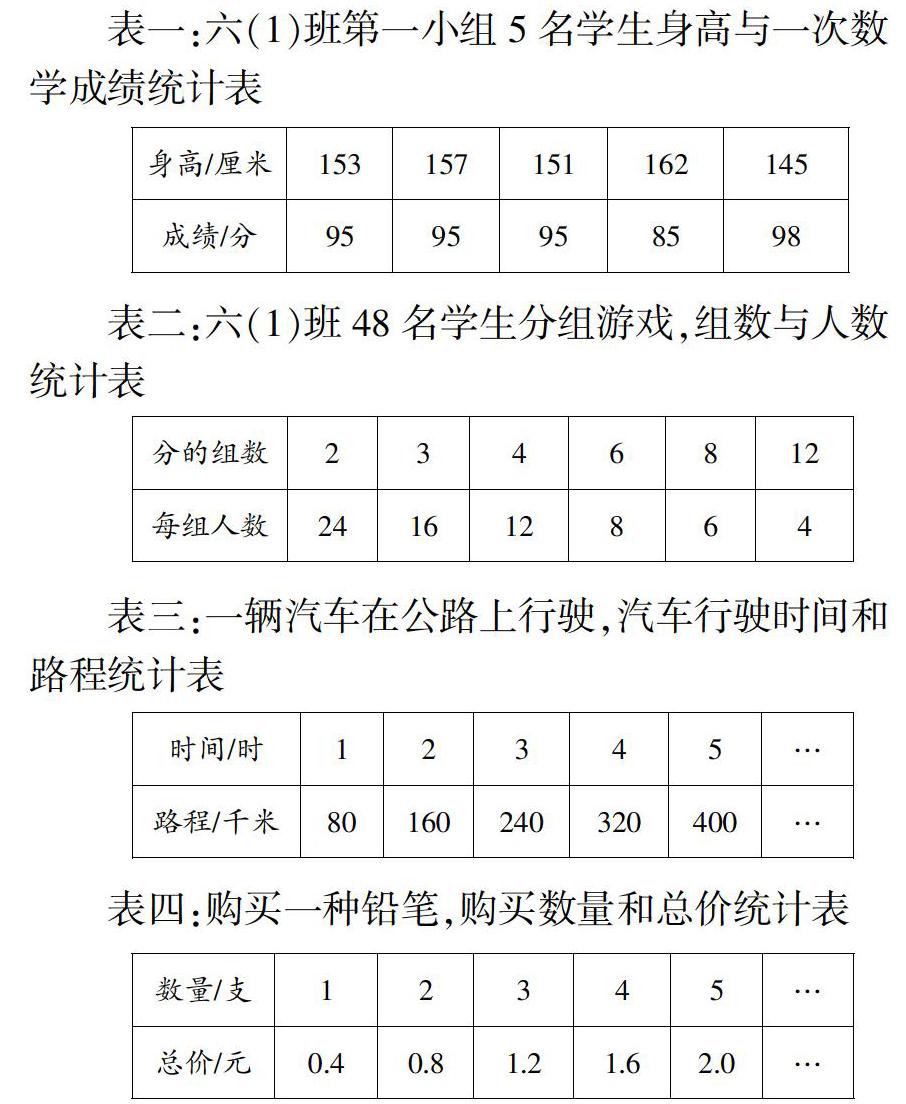
出示四張表格，讓學生找有緊密聯系的兩種量。學生通過討論得出一種量變化，另一種量也隨著變化時，這兩種量就是相關聯量的認識。讓學生體會到這是兩個變量，兩種量變化時有時趨勢相同，有時趨勢相反。

2.理解相關聯的量的變化特點和規律。

根據表二、三、四中數據的特點進行討論，知道每個表格中兩種量都是一種量變化，另一種量也隨著變化。表二中兩種量的積不變，表三和表四中兩種量的比值不變。

3.兩次比較，得出正比例的意義。

經過討論交流，將三個表格分為兩類，接下來進行兩次比較。第一次比較表二與表三、表四的區別。表二中兩種量變化的趨勢相反，乘積一定；而表三和表四中的兩種量變化趨勢相同，比值一定。第二次比較表三和表四的相同之處，即都有兩種相關聯的量，兩種量相對應的比值一定，最后歸納出正比例的意義。

4.深刻理解正比例的意義，建立正比例意義的數學模型。

首先，讓學生在鞏固練習中進一步理解正比例的意義；其次，給出三組相關聯的量，讓學生任意選擇一組或自己想出兩種量，根據要求在表格中填上數據，使得兩種量成正比例。學生在自主討論、填表的過程中深刻理解正比例的意義。

5.了解正比例的意義在生活中的實際運用。

課始，引導學生觀察古人用水鐘計時。學習了正比例的意義后，讓學生用正比例的知識解釋水鐘計時的道理，體會正比例的運用。課尾，通過現代的科學實驗，讓學生體會到正比例的意義的實際應用價值，豐富學生的數學學習情感。

【教學目標】

1.使學生結合具體事例認識成正比例的量，理解正比例的意義，能根據正比例的意義判斷兩種相關聯的量是不是成正比例，并能說明理由。

2.使學生在認識成正比例的量的過程中，體會數量之間的聯系和變化關系，感受表示正比例數量關系及其變化規律的數學模型，滲透函數思想，進一步培養比較、抽象、概括、演繹等思維能力。

3.使學生進一步體會數學與日常生活的密切聯系，了解正比例的意義在生活中的實際應用。

【教學活動及意圖】

一、談話導入，激發興趣

提問：現代人通過鐘表計時，古代沒有鐘表，人們是怎么計時的呢？

動畫演示并說明：這是水鐘的示意圖，上面是出水壺，下面是受水壺，受水壺身有刻度。水從上面的出水壺流入下面的受水壺，人們根據受水壺中水面的高度來確定時間。

追問：水鐘里隱藏著什么數學知識呢？學完今天的知識你就知道了！

【通過動畫演示古代水鐘計時的畫面，激發學生的學習興趣。】

二、引導探究，理解意義

1.理解相關聯的量。

出示四個表格：仔細觀察每個表格中的兩種量，每個表格中的兩種量有聯系嗎？

提問：如果要去掉一個表格，你們選擇去掉第幾個統計表，為什么？

提問：你能說一說其他幾個表格中的兩種量有怎樣的聯系嗎？

整理：表二中總人數不變，分的組數和每組人數在變化。

根據表二中分的組數、每組人數的變化情況，引導學生說出：表二中“分的組數變化，每組人數也隨著變化”；表三中“時間變化，路程也隨著變化”；表四中“數量變化，總價也隨著變化”。

說明：像這樣有緊密聯系的兩種量，在數學上稱為“兩種相關聯的量”。

【觀察表格，學生發現有聯系的兩種量，存在著變與不變的關系。學生體會到當一種量變化另一種量也隨著變化時，這兩種量就是兩種相關聯的量。】

2.研究兩種相關聯量的變化特點和規律。

提問：觀察表二、三、四中的數據，你有什么發現？

（1）觀察表二

師：表二中都是48個人，你能具體說一說分的組數和每組人數的變化規律嗎？

課件演示：分的組數和每組人數是兩種相關聯的量，組數變化，每組人數也隨著變化。

2×24=48 3×16=48 4×12=48……

分的組數×每組人數=總人數（不變）

（2）觀察表三

課件演示：時間和路程是兩種相關聯的量，時間變化，路程也隨著變化。

師：也可以將除法寫成比的形式。

（4）分類比較

提問：同桌討論，現在讓你把這三個表格分分類，你會分成幾類？為什么？

說明：可以分成兩類，表二中是積不變，表三和表四中是比值不變。

師：積不變的時候，你能具體說說兩種量是怎樣變化的嗎？比值不變的時候呢？

說明：表二中一種量變大，另一種量反而隨著變小。表三和表四中一種量變大，另一種量也隨著變大。

說明：今天，我們就來研究變化趨勢相同的兩種量，就是像表三中這樣相對應的兩種量比值不變的情況。

【第一次比較，學生發現兩種相關聯的量在變化時，有的是其中一種量變大，另一種量反而隨著變小，變化趨勢正好相反；有的是其中一種量變大，另一種量也隨著變大，變化趨勢相同。】

（5）比較表三和表四

提問：剛才觀察數據我們知道，時間和路程是兩種相關聯的量，時間變化，路程也隨著變化。除此之外，還有什么相同之處？

【第二次比較，學生發現：兩種相關聯的量在變化時，一種量變大，另一種量隨著變大；一種量變小，另一種量也隨著變小。在變化過程中，比值始終保持不變。】

3.概括正比例的意義。

指出：像這樣，符合上述條件的兩種量，在數學上就叫作成正比例的量，它們之間的關系叫作正比例關系。

鞏固：表四中兩種量成正比例關系嗎？為什么？

提問：怎樣判斷兩種量是不是成正比例？

小結：判斷兩種量是不是成正比例，除了看它們是不是兩種相關聯的量以外，還要看它們相對應的兩個數的比的比值是否一定。

【學生自主交流，教師有序組織得出正比例的意義。】

三、建立正比例意義的數學模型

導入：給你兩種量，你已經能夠判斷它們是不是成正比例關系了，下面加大難度，看看你能不能自己出一道題，讓兩種量成正比例。

1.（1）長方形的寬是1厘米，長和面積。

（2）每套衣服用布2.2米，套數和用布的米數。

（3）每天看書的頁數一定，天數和總頁數。

2.教師以“速度一定，時間和路程”進行示范。先在最左邊這一欄寫上兩種相關聯的量，加上單位。然后寫第一豎行，時間是1小時，路程是80千米，依次類推，在最后一欄寫上省略號。

3.合作要求：（1）同桌兩人任選一題，在表格中填寫兩種量和相關數據，使得兩種量成正比例。

（2）也可以從學過的內容中找出兩種量，填入相關數據，使之成正比例。

反饋：讓學生匯報時先說自己的做法，再說出兩種量為什么成正比例。

提問：像這樣的例子還有很多，能寫完嗎？你能用一個式子概括一下嗎？

說明：在數學上，我們一般用字母x和y分別表示這樣兩種相關聯的量，比值用字母k來表示，這里的比值k必須一定，能寫出怎樣的數量關系式？

提問：這就是正比例關系的表達式，看到這個字母表達式中的x和y，你能想到什么？（變化的量）k呢？（不變的量）

【學生自主選擇兩種量，通過列表寫出對應的數據，使得兩種量成正比例，在探索中深刻理解正比例的意義】

四、鞏固練習

1.生活運用之水鐘計時。

大家還記得剛開始播放的水鐘嗎？誰能用今天學習的知識解釋一下水鐘是如何計時的？

說明：這里有時間和水面的高度這兩種相關聯的量，時間在變化，水面的高度也隨著變化，不變的是每一段時間水上升的高度。

水面的高度÷時間=每一段時間水上升的高度（一定）

說明：根據這個正比例關系式，只要知道水面的高度和每一段時間水上升的高度，就可以計算出經過的時間，古人真是太有智慧了！

2.生活運用之科學實驗。

下面，我們再來看一次真實的科學研究：1996年，鳥類研究者在芬蘭給一只燕鷗套上標志環，通過測試知道燕鷗每天大約飛行200千米。根據燕鷗的遷徙路線，研究者對燕鷗飛行的距離及其到達的地點進行了準確的預測。

提問：預測一下，4個月零10天（約130天）之后，燕鷗大約飛了多少千米？

說明：燕鷗每天大約飛行200千米，這是指燕鷗的速度，也就是速度一定，路程÷時間=速度（一定），路程和時間成正比例關系。

課件出示表格，學生根據天數計算路程。

介紹：計算得到130天飛行了26000千米。確實，4個月零10天后，人們在約2.6萬千米外的澳大利亞發現了那只燕鷗。可見，學習正比例的意義，可以幫助我們在實際生活中進行計算和預測。

【古人的水鐘計時，現代人的科學實驗，都可以用正比例的意義進行合理的解釋，使學生體會到了正比例的意義在生活中的實際應用。】

（作者單位：南京致遠外國語小學）