粗糙集理論在外聘教師教學質量評價中的應用

韓慧蓉

(西安航空學院 理學院，陜西 西安 710077)

?

粗糙集理論在外聘教師教學質量評價中的應用

韓慧蓉

(西安航空學院 理學院，陜西 西安 710077)

應用粗糙集理論對外聘教師的教學質量進行評價。利用粗糙集理論中的屬性簡約和重要度計算對評價指標進行約簡，得到指標的客觀權重，并與主觀權重相結合，給出了教師評價的排序結果。

粗糙集理論；教學質量評價；屬性約簡；客觀權重

0　引言

指標權重是決策分析中的重要數值，是評價和決策中的重要依據，確定權重的方法有很多，粗糙集理論[1-3]就是其中的一種。粗糙集理論[4]是由波蘭華沙理工大學教授帕拉克(Z.Pawlak)在1982年研究不完整數據和不精確知識的表達運用中提出的。它建立在某種分類機制基礎上，把研究對象進行等價劃分，在保持分類基礎不變的情況下，對屬性進行約簡，去掉冗余的屬性，并可以計算出單個屬性的重要度，從而確定各屬性的客觀權重。

1　粗糙集理論[1]

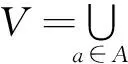
1.1不可辨識關系

對信息系統IS=(U,A,V,f)，則?B?A，不可辨識關系

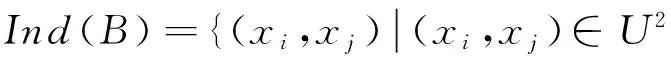
1.2下近似集與上近似集[1]

1.3正域、負域、邊界

1.4冗余和獨立

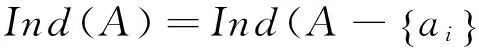
1.5約簡和核[5]

約簡是與信息系統的屬性全集具有相同基本集的最小屬性子集。令信息系統IS=(U,A,V,f)，設B?A，如果B是獨立的，且Ind(B)=Ind(A)，則B是A的一個約簡。屬性的核是信息系統的屬性集合A的所有必要屬性構成的集合，記作core(A)。記red(A)為A的所有約簡集合，那么存在關系core(A)=∩red(A)。

約簡與核是粗糙集理論的兩個基本概念。約簡是一個信息系統的本質部分，與原系統有相同的辨識性，能識別出所有原信息系統可識別的對象。核是所有約簡的共同部分。核和約簡可以通過可辨識矩陣來計算。

1.6可辨識矩陣和可辨識函數

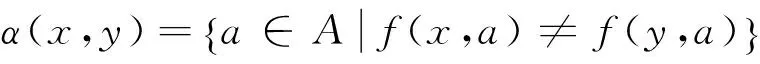
1.7指標的客觀權重

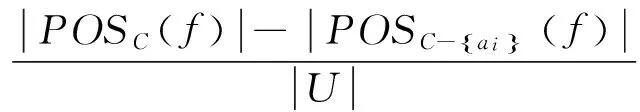
2　粗糙集理論客觀權重分析流程[6-10]

利用粗糙集理論綜合分析客觀權重，首先應建立一個信息系統，然后離散化數據指標，再進行信息系統的屬性約簡，最后確定指標的客觀權重。

3　基于顧客滿意度的指標權重

3.1建立信息系統

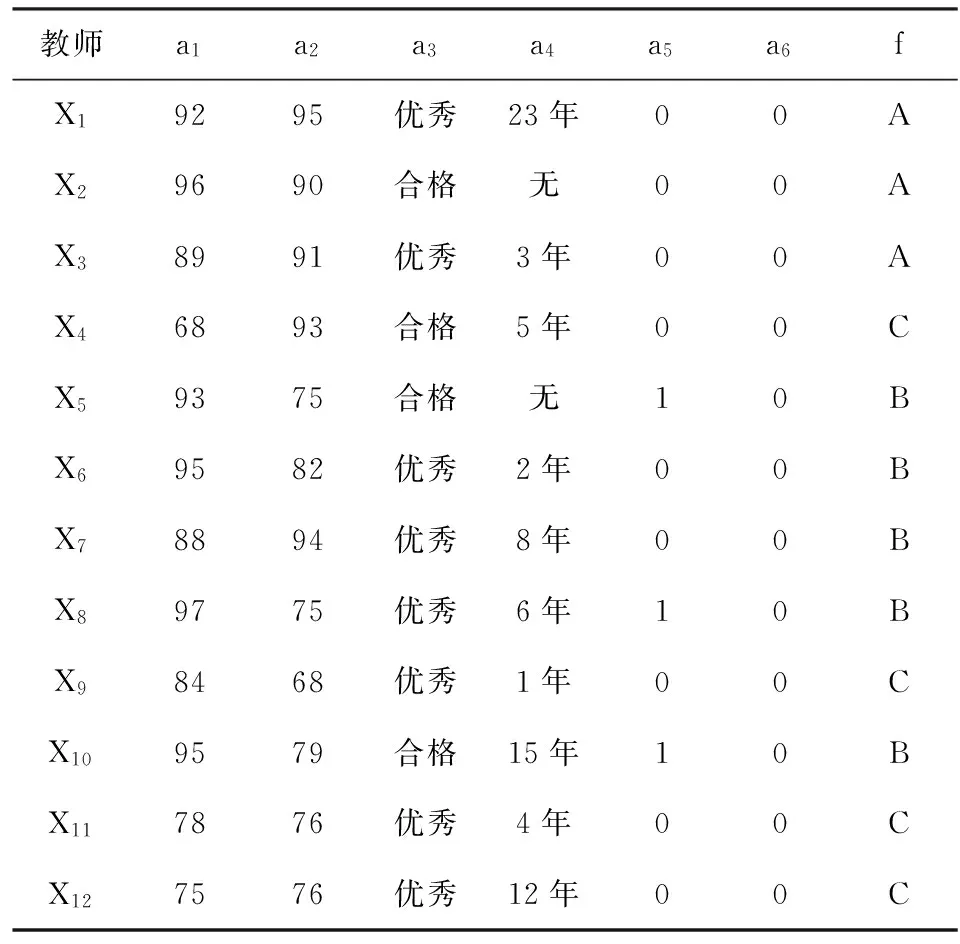
表1　某學校外聘教師各項指標數據信息表

3.2離散化數據

a1，a2：90-100記為1，80-89記為2，70-79記為3，60-69記為4，不及格記為5；a3：優秀記為1，合格記為2；a4：5年以上記為1，1-4年記為2，無教學經驗記為3；a5，a6:“有”記為1，“無”記為0。評價結果f：A記為1，B記為2，C記為3。數據經過離散化處理后，得到表2，即為一個信息系統。

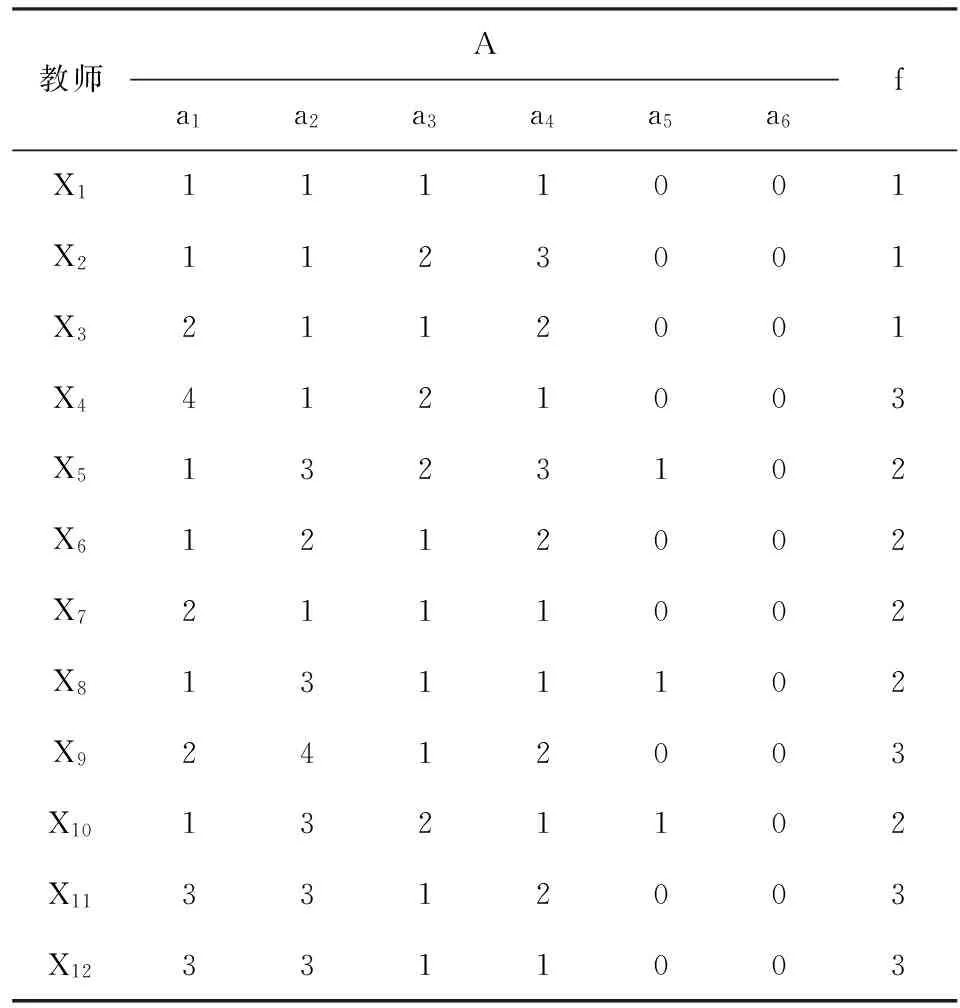
表2　某學校外聘教師各項指標離散化數據信息表

3.3信息系統屬性約簡

為了進行信息系統的屬性約簡，根據表2建立區分矩陣表3。其中每個對象自己和自己不區分。區分矩陣是一個12×12的矩陣，由于篇幅所限，表3只列出其中部分數據。

表3　顧客滿意體驗區分矩陣表

可識別函數

f(A)=(a3∨a4)(a1∨a4)(a1∨a3)…

(a2∨a3∨a5)(a1∨a2∨a4)(a1+a2)…

(a1∨a2)(a1∨a2∨a4)…a4

=a1a2a3a4

3.4各指標的權重[10]

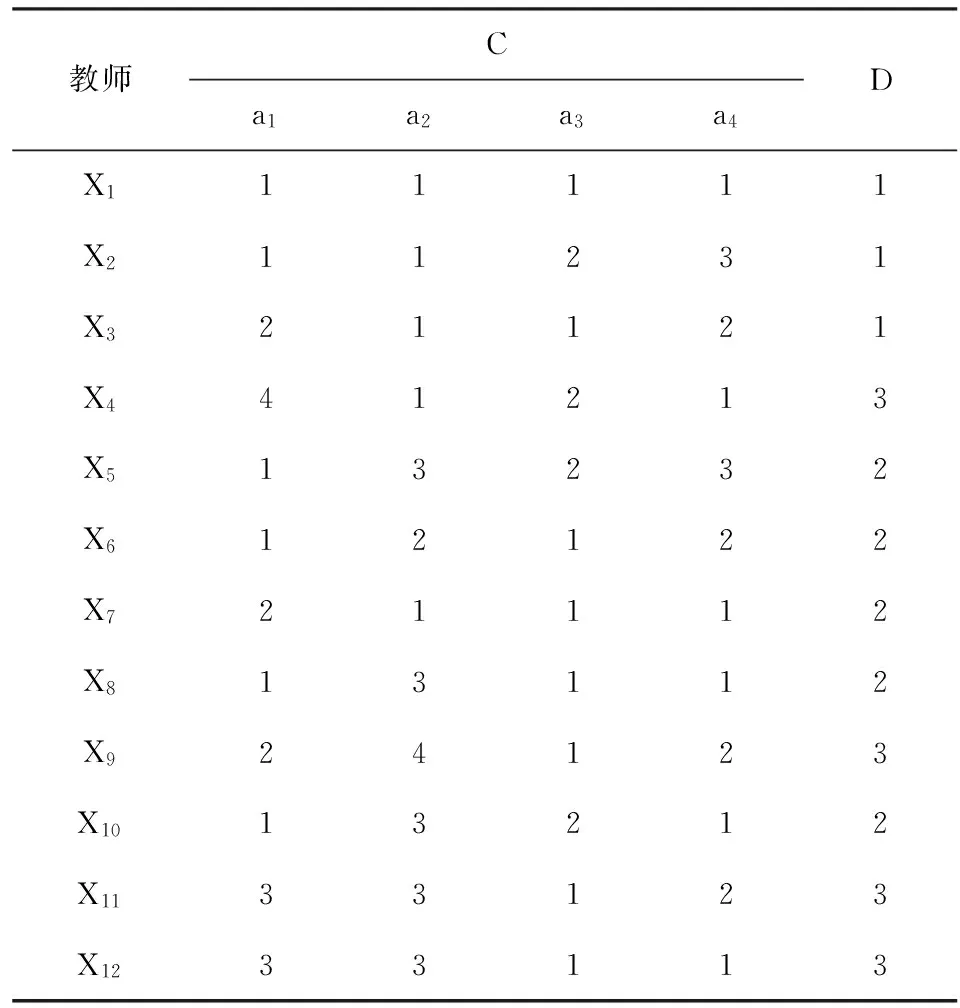
表4　指標約簡外聘教師評價信息表

論域U對于決策屬性D的劃分是：

POSC(D)=U

由公式

=0.333，即a1的重要度是0.333；

同理可得

σCf(a2)=0.5

σCf(a3)=0

σCf(a5)=0.167

歸一化后，得到評價指標中學生評分、學校檢查評分、教學規范程度、教齡的客觀權重分別是0.333,0.5,0,0.167，按照經驗，學生評分、學校檢查評分、教學規范程度(優秀按照90分計，合格按照80分計)、教齡，有無調停課、有無教學事故分別的主觀權重分別是0.3,0.2,0.1,0，并按照主觀權重和客觀權重分別占30%，70%，對每位外聘教師賦分值，得到12位外聘教師x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12的分值分別74.0639,70.3176,69.1166,63.0853,63.1983,67.2483,70.608,65.4921,57.8373,67.238,59.5294,59.4953，排序結果是x1,x7,x2,x3,x6,x10,x8,x5,x4,x11,x12,x9。

4　結論

通過以上分析，原有的教師評價結果更依賴于主觀判斷，在教師人數較多時評價結果不夠準確，也可能會出現偏差，例如教師X7，原評價結果是B，而計算排序結果是第二名。利用粗糙集給出評價指標的客觀權重，并與主觀權重相結合，既有效避免了主觀偏差，又克服了客觀權重在信息不明確的情況下出現的數據失真，所以更準確、更具有說服力。

[1] 張文修.粗糙集理論與方法[M].北京：科學出版社，2001:2-13.

[2] 苗奪謙，李道國.粗糙集理論、算法和應用[M].北京：清華大學出版社，2008:82-122.

[3] 王彪，段禪倫，吳昊，等.粗糙集與模糊集的研究及應用[M].北京：電子工業出版社，2008:2-30.

[4] Pawlak Z.Rough Set[J]Internationgnal Journal of Computer and Information Science,1982(11):341-356.

[5] 張文修.粗糙集屬性簡約的一般理論[J].中國科學(E輯 信息科學)，2005，35(12):1304-1313.

[6] 盧鵬，吳健樂.粗糙集層次分析法在學生綜合評價中的應用[J].宜賓學院學報，2015，15(6):103-107.

[7] 韋良.粗糙集理及其應用于發展研究[J].電腦知識與技術，2008，4(1):172-174.

[8] 韓禎祥，張琦，文福拴.粗糙集理論及其應用綜述[J]，控制理論與應用，1999，16(2)：153-155.

[9] 李永敏，朱善軍，等.基于粗糙集理論的數據挖掘模型[J]，清華大學學報(自然科學版)，1999，39(1)，110-113.

[10] 孫斌，王立杰.基于粗糙集理論的權重確定方法研究[J]，計算機工程與應用，2006(29)：216-217.

[責任編輯、校對：周千]

Application of Rough Set Theory to the Teaching Quality Evaluation of Part-time Teachers

HANHui-rong

(Faculty of Science,Xi'an Aeronautical University,Xi'an 710077,China)

The rough set theory is applied to the teaching quality evaluation of part-time teachers.Attribute reduction and importance calculation in the theory are employed to reduce evaluation indexes.Their objective weights are obtained,and combined with subjective weights to produce the sorting result of part-time teachers.

rough set;teaching quality evaluation;attribute reduction;objective weight

2016-07-04

韓慧蓉(1971-)，女，山西盂縣人，副教授，從事基礎數學方面的研究。

O221.6

A

1008-9233(2016)05-0065-04