基于TVP-VAR模型的利率變動與股市波動的時變關系研究

胡一博

（西北工業大學 自動化學院，陜西 西安710072）

基于TVP-VAR模型的利率變動與股市波動的時變關系研究

胡一博

（西北工業大學 自動化學院，陜西 西安710072）

采用時變參數向量自回歸模型，實證研究了利率、股價與股市波動率三者之間的動態時變聯動關系。研究結果表明：利率變動對股票市場在不同時期的影響不同；利率變動對股票市場的短期結構沖擊顯著；同時研究還發現我國股市具有較強的投機性。

利率；股市；TVP-VAR模型

在實際經濟運行過程中，利率變動對股票市場具有直接、迅速的影響。分析利率變動與股市波動之間的時變關系，有利于把握貨幣市場與股票市場間的動態聯動關系，為貨幣當局更好的利用利率政策調控股市提出更具價值的政策建議。傳統的現值模型把利率與股價的關系描述為P=D/R, 其中P為股票價格、D為股息收入、R為利率。傳統經濟理論認為股票價格與利率成反比。然而近些年，越來越多的經濟學家和學者運用向量自回歸（VAR）等計量模型對這一問題進行研究。Bernanke[1]等運用VAR模型通過對美國股市的研究發現，當聯邦基金利率每下調0.25%，就會引起股票價格1%的增加。而Alatiqi[2]等運用VAR模型對美國利率變動與股市波動的相關關系進行分析，得出利率變動對股市波動影響不顯著的結論。Basisth[3]和Mayes[4]等學者的研究則發現，利率政策對股票價格的影響并不確定，利率與股價的相關關系與經濟周期的變動有關。

縱觀在這一研究領域已有的文獻，大多數都采用傳統計量模型進行實證研究，且結論并不一致。而較多的研究方法，如向量自回歸，都是假設模型參數不隨時間變化。但由于研究時間跨度較大，隨著時間的推移，經濟周期、政策偏好和其他經濟變量等因素不斷發生變化，模型參數不可能保持不變。所以本文使用帶有時變參數的向量自回歸模型（TVP-VAR）對這一問題進行分析，是本文的創新點所在。

一、數據說明與理論模型

（一）數據的選取及處理

由于我國在2005年4月進行了股權分置改革，股市監管更加嚴格，也更加市場化。為避免以往數據的干擾，本文選取了從2005年4月到2015年8月的利率、股價和股市波動率的月度數據作為樣本進行研究，共125組數據。

本文選用銀行間7天同業拆借利率作為利率政策的代理指標，并取月對數增長率。在反映股市波動方面本文選取兩個指標：在反映股票價格變化方面，本文選取滬深300價格指數，并取月對數收益率,即It=lnIt-lnIt-1；在反映股市波動率方面選取的指標是日收益率的標準差，并用移動平均法計算月度數據，所有數據均來自WIND數據庫。本文采用ADF單位根檢驗，對所有數據的平穩性進行分析。結果表明，三個變量都是平穩的時間序列，均不存在單位根，滿足構建TVP-VAR模型的要求。

（二）理論模型

Nakajima為了允許截距項、方差以及VAR系數都可以隨時間變化，對向量自回歸模型提出了一套新的算法，形成了TVP-VAR模型。該算法把一個標準的VAR模型進行了如下變化，首先定義一個標準的VAR模型為：

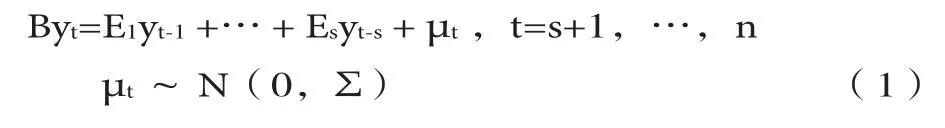
其中B為p×p維聯立系數矩陣，yt為p×1維觀測向量，E1…Es是p×p維滯后系數矩陣，模型中擾動項μt為p×1維結構性沖擊。假定結構沖擊間的關系服從遞歸識別，即矩陣B為下三角陣，模型（1）可整理為：

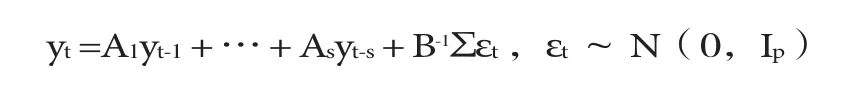
其中Xt是通過單位矩陣和變量向量滯后期向量的克羅內克乘積所構建的矩陣，βt、Bt、∑t表示三個具有時變性的狀態方程，分別為自回歸系數矩陣、同期關系系數矩陣和方差-協方差矩陣。設bt=(b21，b31，b41，…，bp，p-1) ′為 Bt下三角矩陣的堆棧，設ht為矩陣∑t的下三角部分向量。參數服從隨機游走過程，該模型的動態變化是由以下公式決定：βt+1=βt+μβt，bt+1=bt+μbt，ht+1=h1+μht，并且存在如下關系：

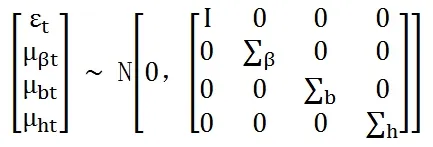
本文采用20000次MCMC抽樣實現對參數βt、Bt、∑t的估計1，并基于125組樣本抽樣做出下文中的統計推斷。

二、實證分析結果

（一）TVP-VAR模型的參數估計結果

表1中參數檢驗的Geweke值均未超過5%的臨界值1.96，這表明Geweke統計量在95%的置信度水平下，不能拒絕參數收斂于后驗分布的原假設。無效因子值表示為得到不相關樣本所需要抽樣的次數，也就是說，無效因子的數值越小表示樣本越有效。表1中參數的無效因子值均小于90，表明本文所使用的125組數據的預測模擬可以使MCMC模擬收斂。

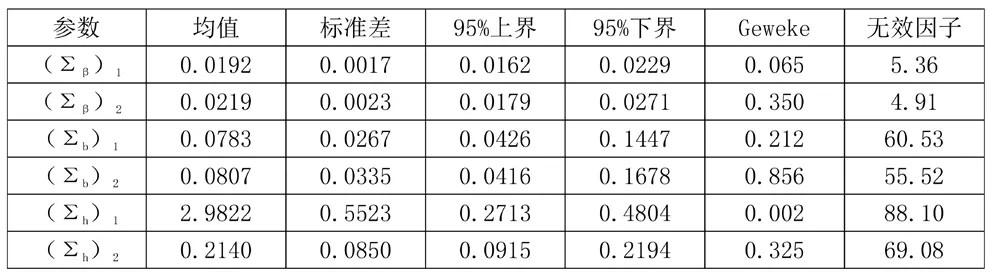
表1 TVP-VAR模型的參數估計結果及診斷

（二）時變參數的特征分析

在參數不變模型向量自回歸模型中，模型估計后參數都只有一個估計值。但在TVP-VAR模型中，每個參數的估計值都是隨時間變化的。圖1展現了模型中 Sβ1，Sβ2，Sb1，Sb2，Sh1，Sh2這 6 個參數的樣本抽樣模擬路徑。參數的模擬路徑體現出明顯的波動聚類現象，并且在模擬尾部各參數均收斂于樣本均值的估計結果。

圖1 時變參數的特征

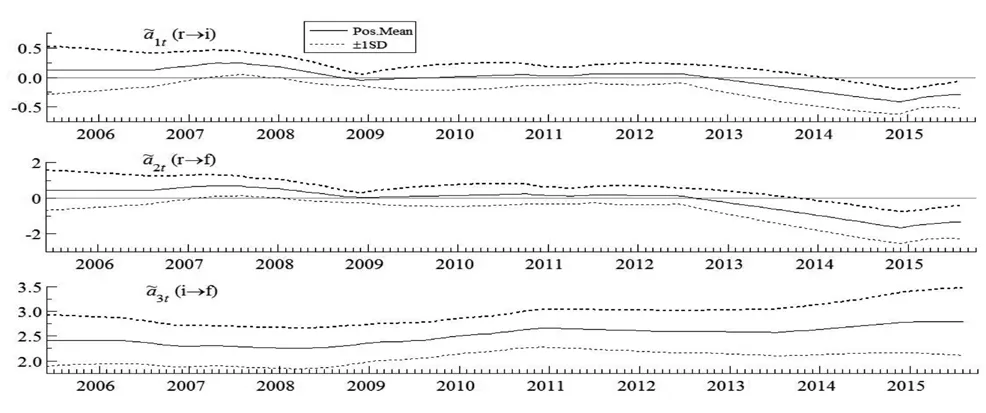
圖2 變量同期關系的時變特征

圖3 不同時滯期的脈沖響應圖

（三）利率、股價、股市波動率相互影響關系的時變特征分析

圖2描述了利率，股價，股市波動率之間的動態聯動時變關系。由圖2中的第1個子圖可見，利率在不同時期對股價的影響是截然不同的。在2009年之前，利率對股價的影響系數?（r→i）為正，2009年至2013年之間利率對股價的影響系數接近0值，而2013年以后利率與股價呈負相關關系，且在2015年前后影響系數接近-0.5。由此看來利率對股價的影響在近10年內經歷了一個正相關→不相關→負相關的周期。結合2013至2015年利率下調后股市的表現，本文發現利率與股票價格有顯著的負相關關系，這表明利率政策對股票市場的傳導渠道正逐步暢通。第2個子圖反映了利率對股市波動率的時變影響?（r→f），這一圖形與子圖1相似，這一表現也與客觀經濟規律相符。第3個子圖反映了股價對股市波動率的影響，影響系數?（i→f）在近10年來均大于2，由此可見股價變動對股市波動率有較大的影響，并且這種影響關系在2009年后保持持續上升的態勢。

（四）利率、股價、股市波動率在不同時滯期的脈沖響應分析

對于TVP-VAR 模型，可以設置不同的滯后期數，這樣在針對各變量間的脈沖響應進行分析時，可以清晰的反映單位沖擊變量對被沖擊變量在不同滯后期形成的影響。為了描述不同時期利率對股市的影響情況，本分分別選取1個月（短期沖擊）、3個月（中期沖擊）和6個月（長期沖擊）的標準正向沖擊形成三種時期的脈沖響應時間序列圖。圖3的三個子圖中，實線分別代表了利率對股價（εr→i）、利率對股市波動率（εr→f）、股價對成股市波動率（εi→f）在不同時期的短期結構沖擊關系。而虛線部分別代表的是三者中期和長期的結構沖擊關系。通過比較可以發現，利率對股價和股市波動率的短期結構沖擊顯著，而中長期結構沖擊相對不顯著；而股價對股市波動率的結構沖擊同樣為短期顯著。

三、結 論

本文構建了一個含有利率、股價和股市波動率的TVP-VAR模型，分析了三者之間的動態時變聯動關系，可以看出時變模型可以更好的解釋利率變動與股市波動的相關關系，也與實際情況相符。通過上文分析可以發現，近10年我國利率變動與股市波動經歷了正相關、不相關和負相關的一個周期，這也體現出了貨幣政策的利率政策傳導渠道在逐步暢通。利率調控手段相對傳統的靠貨幣供應調控，具有迅速、直接等特點，但同時也應注意在運用利率政策調控時需充分考慮其對股市造成的影響。

通過上文對不同時期的脈沖響應沖擊分析可以看出，利率對股市的沖擊主要表現為短期效應，利率對股市的中長期影響不顯著。同時，研究還發現股價對股市波動率的影響系數較大，而且保持持續上升趨勢。股市波動率過高是股市不成熟、不穩定的表現，也是造成股災的主要原因。在中國股票市場上，投資者們盈利的主要方式就是價低時買入、價高時賣出，從中賺取利益，投資者很少關注于時間價值投資，股價上漲靠題材，而利率作為股市的“風向標”恰恰在這時發揮了關鍵作用。然而利率下調后股價迅速的上漲和股市過高的波動率，容易產生集群效應，從而引發股災，并對實體經濟產生不利影響。綜上所述，我國政府在運用利率政策調控時需充分考慮其對股市造成的影響，引導股市健康的發展。

[1]Ben S Bernanke,Kenneth N Kuttner.What Explains the Stock Market’s Reaction to Federal Reserve Policy[J].The Journal of Finance, 2005 ,60(3): 1221-1257.

[2]Alatiqi.The Impact of Monetary Policy Shocks on Stock Prices[J].Journal of International Money and Finance,2008,29(5):879-896.

[3]Basistha A ,Kurov.Macroecnonmic Cycles and the Stock Markets Reaction to Moneraty Policy[J].Journal of Banking and Finace,2008,32 (12):2606-2616.

[4]Mayes.Dynamic Linkages between Monetary Policy and the Stock Market[J].Economic Inquiry,2012, 73(3):171-193.

F224.12

A

1003-1154(2016)01-0007-03

10.3969/j.issn.1003-1154.2016.01.003

國家社科基金青年項目（15CJY034）.

1 具體算法參見Nakajima(2011) TVP-VAR手冊