例談函數零點問題解決策略

石家文

例談函數零點問題解決策略

石家文

函數零點的相關問題涉及函數方程，蘊含轉化化歸、數形結合、分類整合等數學思想，是函數與方程知識的綜合應用之點，也是高考的重點、難點和熱點。筆者通過多年的教學體會和對近年來高考試題的分析，從五個方面談一談函數零點相關問題的解決辦法，供老師們參考。

一、零點算出來

當問題的實質是求函數零點或導函數零點時，別無選擇，必須把零點用解方程的辦法算出來。

解得3x-1=3或3x-1=-3（舍），

解得3x=4，

所以x=log34。

說明：函數f（x）的零點就是使f（x）=0的x的值，也就是關于x的方程f（x）=0的根，常用求方程根的方法計算函數的零點。

二、零點畫出來

如果問題只涉及零點的個數，可考慮用零點畫出來的方法，但要注意函數圖像必須是能夠畫得出來的。畫初等函數的圖像，學生不會有難度。如果是畫較復雜函數的圖像，可以以導數為工具，先分析函數的單調性和極值等，再畫出函數的圖像。

例2.設函數f（x）=（x-2）ex+a（x-1）2，（1）若f（x）有兩個零點，求a的取值范圍；（2）略。

解：（1）由f（x）=0?a（x-1）2=（2-x）ex，顯然x=1時，a不存在，故x≠1。所以

當x＞1時，g′（x）＞0；當x＜1時，g′（x）＜0。函數g（x）在（-∞，1）內單調遞減，在（1，+∞）內單調遞增。

又x≥2時，g（x）≥0；x＜2時，g（x）＜0，且g（0） =-2。故在同一坐標系中作直線y=-a，函數y=g（x）的圖像如圖1所示。由圖知：當且僅當-a＜0，即a＞0時，直線y=-a與函數y=g（x）的圖像有兩個交點，故a的取值范圍為（0，+∞）。

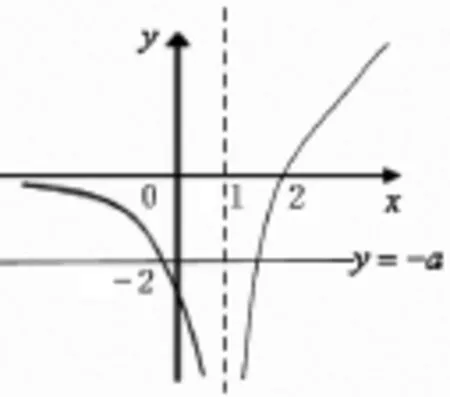
圖1

說明：本題用零點畫出來的方法，比參考答案簡單多了，真是一個圖形勝過千言萬語！數形結合是避開分類討論的最好辦法。

三、零點畫出來與算出來相結合

當問題的題設給出的函數是分段函數（或轉化后為分段函數），而問題的解決用到該函數的零點時，可采取先把零點畫出來，再把零點算出來的方法，來一個雙管齊下。

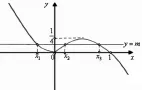
圖2

又x1是關于x的方程2x2-x=m，即2x2-x-m=0的較小根。

說明：本題由于是一道小題，原供參考答案是利用圖像與不等式方法得到相應結果。筆者在教學中發現將該題改為小題大做，把x1·x2·x3用m表示出來，用函數思想求x1·x2·x3的范圍，是一道極佳的函數方程的問題。

四、零點反串

若題設中已給出了函數零點的字母表示，而目標中又涉及零點的相關代數式時，或需用零點來聯系相關的參數時，必須回歸函數零點的定義。筆者將其稱之為零點反串。

例4.已知函數f（x）=（x-2）ex+a（x-1）2有兩個零點。（1）略；（2）設x1，x2是f（x）的兩個零點，證明：x1+x2＜2。

解：（2）不妨設x1＜x2，由（1）及圖3知：x1＜1＜x2，進而有2-x2＜1。所以x1，2-x2∈（-∞，1）。

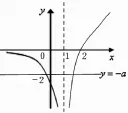
圖3

由f′（x）=（x-1）（ex+2a）及a＞0知：

當x∈（-∞，1）時，f′（x）＜0恒成立，所以f（x）在（-∞，1）內單調遞減。

所以x1+x2＜2?x1＜2-x2?f（x1）＞f（2-x2）?f（2-x2）＜0。

由于f（2-x2）=-x2e2-x2+a（x2-1）2，而f（x2）=（x2-2）ex2

+a（x2-1）2=0，所以f（2-x2）=-x2e2-x2-（x2-2）ex2

。

設g（x）=-xe2-x-（x-2）ex，而g′（x）=（x-1）（e2-xex）。所以當x＞1時，g′（x）＜0，而g（1）=0，故當x＞1時，g（x）＜0，從而g（x2）=f（2-x2）＜0，故x1+x2＜2。

說明：本題雖然是一道利用函數單調性證明不等式x1＜x-x2的問題，但最關鍵的地方是利用x1，x2的反串，得f（x1）=0，f（x2）=0，成功地消掉了x1及a，為問題的解決奠定了基礎。

五、設而不求

如果函數是一個超越式，我們無法直接解出其零點。但由零點存在性定理或作圖知道設函數在某一區內有零點時，我們可采用先設零點再反串的方法予以解決。

例5.設函數f（x）=e2x-alnx。

（1）討論f（x）的導函數f′（x）零點的個數；

當a＞0時，方程g（x）=a有一個根，即f′（x）存在唯一零點；

當a≤0時，方程g（x）=a沒有根，即f′（x）沒有零點。

（2）由（1），可設f′（x）在（0，+∞）的唯一零點為x0。當x∈（0，x0）時，f′（x）＜0；當x∈（x0，+∞）時，f′（x）＞0。故f（x）在（0，x0）單調遞減，在（x0，+∞）單調遞增，所以f（x）min=f（x0）。

由f′（x）=0得0，進而得①和

以函數零點相關問題作為高考壓軸大題，就是因其綜合性極強，思想內涵豐富，有很好的選拔功能，有難度是必然的。但只要我們用活五大招，從數與形兩方面思考，學生破解這類問題應該沒有問題。

（作者單位：永順縣第一中學）