清晰完整話歸納

張翠萍

歸納法是從觀察、實驗和調查所得的個別事實中抽象概括出具有普適性的一般原理的一種思維方式或推理形式，其主要環節是歸納推理。如何才能使得歸納清晰且完整呢？筆者在教學中做了如下嘗試。

一、借助直觀，清晰歸納

幾何直觀通過圖形描述和分析把復雜的數學問題變得簡明、形象，在推理教學中經常會用到幾何直觀來明晰思路。

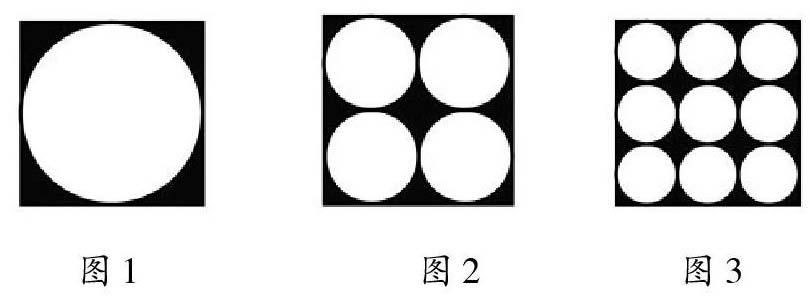
筆者在執教人教版《數學》六年級上冊《圓的周長與面積計算》時，出示了這樣一道思考題：有三個邊長都是6厘米的正方形，第一個正方形里畫1個最大的圓，第二個正方形里畫4個相同的盡量大的圓，第三個正方形里畫9個相同的盡量大的圓，問這幾個正方形中圓的面積之和占正方形面積的百分之幾？剛開始有學生猜想9個小圓的面積一定比1個大圓的面積大，也有學生反駁。筆者沒有給出定論，而是引導學生先在稿紙上畫出示意圖，畫圖的過程中學生發現，要想得到面積最大的圓，圓的半徑必須最長。根據題意，在第一個正方形中應畫一個以正方形的中心為圓心，以正方形的邊長的一半為半徑的圓（如圖1）。要畫4個盡可能大的圓，應先將正方形分成4個等大的小正方形，再以小正方形的中心為圓心，以小正方形的邊長的一半為半徑畫出4個等大的圓（如圖2）。以此類推，要畫9個等大的圓，需要先把正方形分割成9個等大的小正方形，再畫出如圖3所示的9個等大的圓。根據圖示還無法一眼看出三幅圖中圓的面積關系，不過借助圖示可以知道圓的半徑。通過計算，學生發現第一個正方形中大圓的面積是3.14×（6÷2）2=3.14×9，第二個正方形中四個小圓的面積之和是3.14×（6÷2÷2）2×4=3.14×9，第三個正方形中9個小圓的面積之和是3.14×（6÷3÷2）2×9=3.14×9。至此，學生發現原來這幾幅圖中圓的面積之和是相等的。這時有學生提出如果第四個正方形中有16個相同的盡量大的小圓，第五個正方形中有25個相同的盡量大的小圓，它們的面積之和還相等嗎？筆者肯定了該學生的大膽質疑并引導全班學生共同探討，學生們借助直觀圖形，再次計算驗證了這一結論，并總結出依次在正方形中取n2個相同的盡量大的小圓，其面積之和相等。

以上教學中借助幾何直觀，學生形成了猜想，再通過計算推翻猜想，推導出了正確結論。學生通過自主探究，不斷猜想、驗證、反思，發現圖形之間的內在聯系，尋找規律，探尋本質，獲得深刻理解。

二、巧妙設計，完全歸納

在小學階段，主要學習合情推理，即歸納推理和類比推理。歸納推理又多表現為不完全歸納推理。不過，一些教學素材也可以實現完全歸納推理。教師通過巧妙的教學設計，能幫助學生建立完全歸納推理的意識。

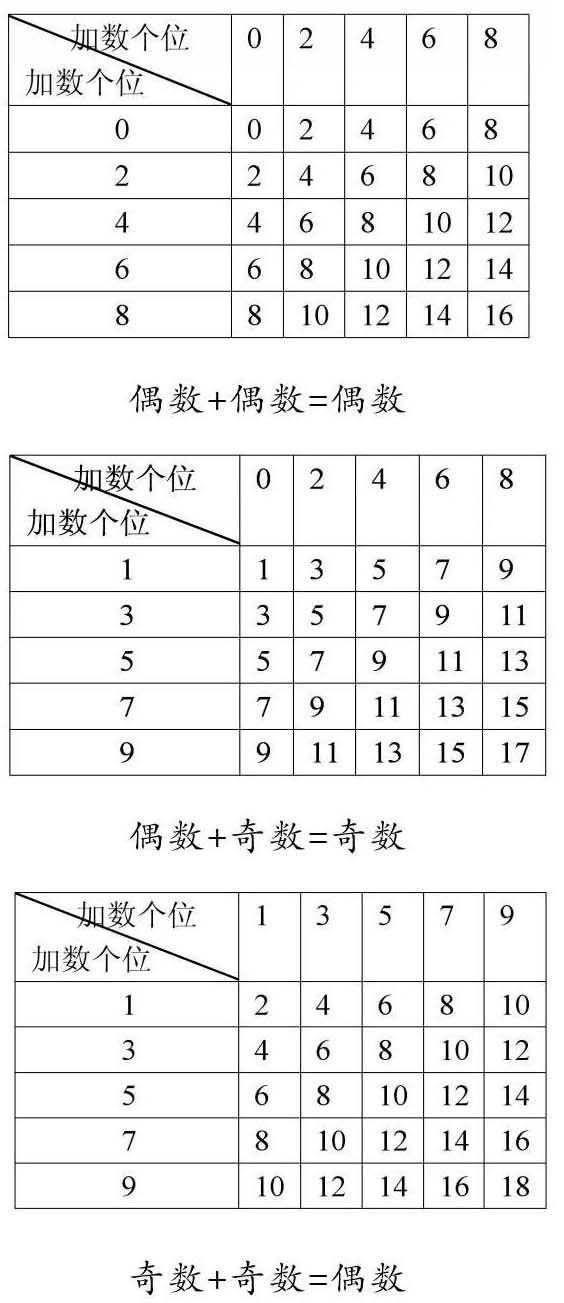
筆者借用蘇教版《數學》五年級下冊《和的奇偶性》的教學談談具體做法。課前，教師創設問題情境，與學生一起回顧一個數的奇偶性的判斷定理：判斷一個數是奇數還是偶數，只需要看它的個位，個位是1、3、5、7、9的數是奇數，個位是0、2、4、6、8的數是偶數。之后，又讓學生判斷兩個數相加所得和的奇偶性，如：213214218+847645147所得的和是奇數還是偶數？學生根據它們的個位8加7等于15，推斷出這兩個數的和是奇數。以此為基礎，筆者引導學生繼續判斷任意兩個自然數相加所得和的奇偶性。為了便于研究，筆者先讓學生將任意兩個自然數相加的情況進行分類，有學生認為大致可以分為三類：偶數+偶數；奇數+奇數；偶數+奇數。這時，有學生提出，還有另外一種情況：奇數+偶數，應該是四類。正在他們僵持不下之際，有學生提出，根據加法交換律，“奇數+偶數”與“偶數+奇數”所得的和是一樣的，所以還是只有三種情況。那么，它們的和又分別是奇數還是偶數呢？剛開始，學生的猜測是：偶數+偶數=偶數；奇數+奇數=奇數；偶數+奇數=奇數。如何驗證呢？學生想到舉例。如何舉例才能窮盡所有的可能呢？由于判斷一個數是奇數還是偶數只要看這個數的個位，所以只要舉一位數加一位數的例子就可以了。也就是說可以用個位是0、2、4、6、8的數來代表所有的偶數，用個位是1、3、5、7、9的數來代表所有的奇數。它們相加后的所有可能可以用以下三個表格來概括。

從以上三個表格中可以清晰地看出偶數+偶數=偶數；偶數+奇數=奇數；奇數+奇數=偶數。筆者引導學生從整體入手先分類再猜想，讓他們掌握了從復雜問題中找出關鍵要素進行有序思考的方法，從而提升了他們完全歸納推理的能力。

（作者單位：云夢縣義堂中心小學）