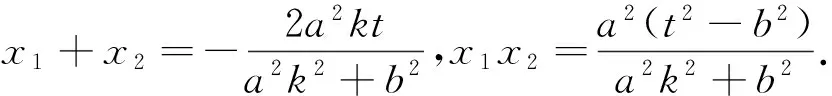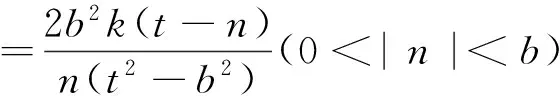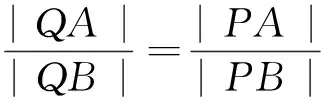對一道高考解析幾何試題的探究
邱麗玉
福建省莆田第五中學 (351100)
?
對一道高考解析幾何試題的探究
邱麗玉
福建省莆田第五中學(351100)
2015年全國高考四川卷(理)題20是:
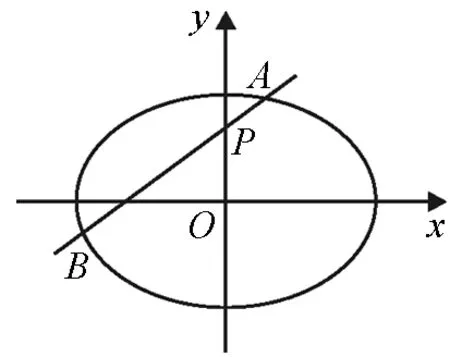
圖1
這道試題內涵豐富,值得探究,不應解完即止,可作為探究性學習的素材,引導學生深入探究,充分挖掘其豐富的內涵和潛能.
一、縱向探究:由特殊到一般的探究
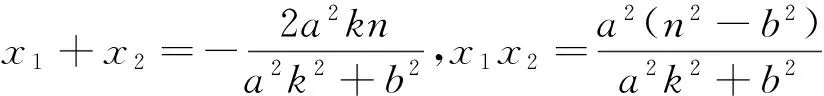
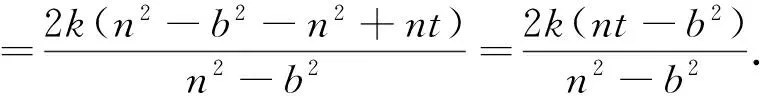
由以上探究過程易知,當點P的縱坐標n滿足-b 類似地,容易得到關于雙曲線的類似性質: (1)當k=0時,分別求C在點A和B處的切線方程; (2)y軸上是否存在點Q,使得當k變動時,總有∠OQA=∠OQB?說明理由. 問題3結論1.1、2.1、3.1的逆命題是否成立? 易知P為定點(0,n)(0<|n| 類似地,容易得到結論2.1、3.1的逆命題: 以上引導學生從縱向、橫向、逆向三個方面對上述高考試題進行探究,把隱藏在題目背后的問題本質進行挖掘與拓展,得到了一系列對學生來說是全新的結論.正如著名數學教育家G·波利亞所倡導的:“一個專心的認真備課的教師能拿出一個有意義的但又不太復雜的題目,去幫助學生發掘問題的各個方面,使其通過這道題,就好像通過一道門戶,把學生引入一個完整的理論領域”.通過探究,學生發現問題、分析問題、解決問題的能力,以及創造性思維能力得到了鍛煉和提高,這正是素質教育所要追求的.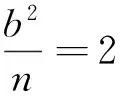
二、橫向探究:由橢圓到雙曲線、拋物線的探究
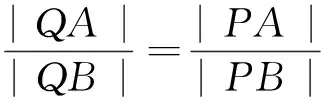
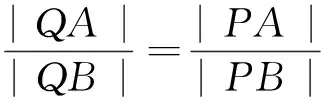
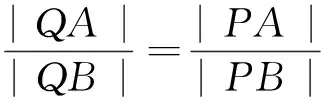
三、逆向探究:由原命題到逆命題的探究