2016高考數學全國甲卷(Ⅱ卷)壓軸題的解法分析

呂　鵬

重慶市朝陽中學　(400700)

?

2016高考數學全國甲卷(Ⅱ卷)壓軸題的解法分析

呂鵬

重慶市朝陽中學(400700)

2016高考數學全國甲卷(Ⅱ卷)壓軸題(第21題)為：

這是一道函數與導數、不等式結合的綜合題型，題目簡潔，直面問題，既能很好的考查考生的基礎知識，又具有很好的區分度. 題目的解法可從多角度展開，能很好的體現高中數學新課程的理念.

一、第(Ⅰ)問的解法分析

第(Ⅰ)問分為兩部分，先求單調性，然后證明，對于后半部分的證明，可根據前半部分的結構特征，利用單調性而得.也可通過構造函數單獨證明.具體過程如下：

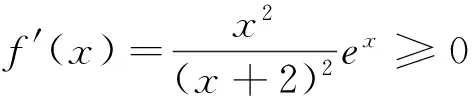
(-∞,-2)和(-2,+∞)時，f(x)單調遞增.下面證明：當x>0時，(x-2)ex+x+2>0.

證法2：令I(x)=(x-2)ex+x+2，I′(x)=(x-1)ex+1，I″(x)=xex>0，故I′(x)單調遞增.當x>0時，I′(x)>I′(0)=0，從而I(x)單調遞增，I(x)>I(0)=0，即(x-2)ex+x+2>0.

評析：本小問前半部分考查通過導數判斷函數的單調性，導數的運算法則，其中導數大于等于零，考生容易誤認為大于零，單調區間的表示很多考生容易誤寫成“(-∞,-2)∪(2,+∞)”.看似簡單，實則對學生基礎知識的掌握程度要求較高.

二、第(Ⅱ)問的解法分析

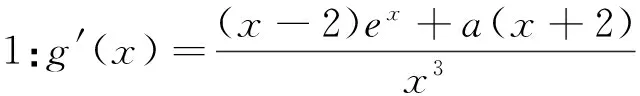
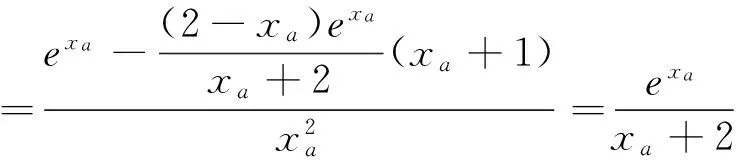
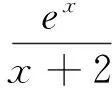
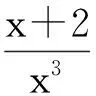
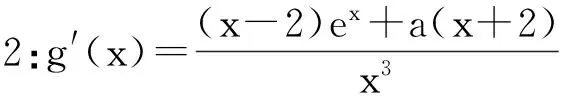
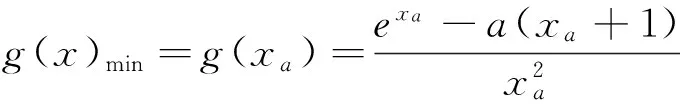
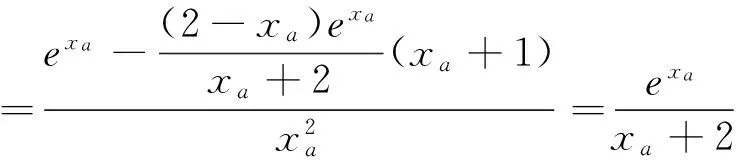
評析：解法2與解法1的區別在于兩方面，一方面對g′(x)的處理較常規，即判斷分子的符號，若判斷不易，則繼續求導，直至易判斷為止.另一方面是通過a的范圍結合單調性求得xa的范圍，這樣求得的值域與a的范圍是對應的.另外，解法1，解法2都是直接求g(x)的最小值，將x視為主元，事實上本題中，有兩個變量x和a，求最小值不妨將a視為主元，會收到意想不到的效果，由此，可得下面解法.

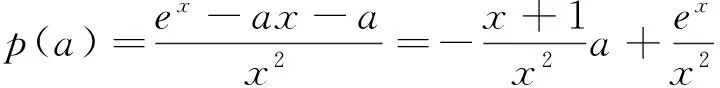
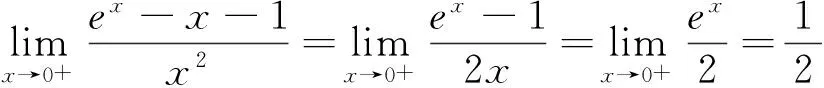
三、解法3的再思考

如圖1，當a在[0,1)之間變化時，g(x)的圖像

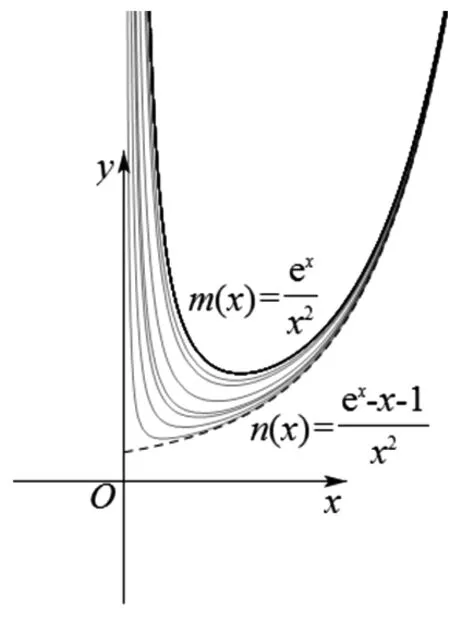
圖1

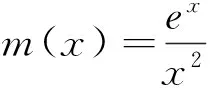
多元問題，我們平時要敢于突破傳統思維定式，視不同的未知數為主元.另一方面，要自覺進行相關思維訓練，擴展思維角度.特別要學會在事物對立面的統一中轉換思維，多方位的思考數學問題，才能有效地提高解題能力.