反時限過流保護整定優化研究
黃 超, 楊 彥, 田君楊
(廣西電網電力調度控制中心,廣西南寧530023)
?
反時限過流保護整定優化研究
黃超, 楊彥, 田君楊
(廣西電網電力調度控制中心,廣西南寧530023)
反時限過流保護因動作曲線配合困難掩蓋了其在原理上緊密反映短路電流變化的固有優勢,一定程度限制了其應用。為此,在深入分析保護動作曲線之間嚴格配合的基礎上,從保護選擇性角度提出了反時限過流保護之間、反時限保護與定時限保護、定時限保護與反時限保護的整定配合原則;并在保證靈敏性的前提下,采用壓縮因子粒子群優化算法(K-PSO)、輔之曲線參數與選擇性配合作為約束條件,從快速性角度建立了整定范圍內的時間優化目標。整定原則與優化模型可分別用于反時限過流保護整定計算與定值優化,有助于提高國內反時限過流保護的工程實用價值。算例分析驗證了該方法的有效性與可行性。
反時限過流保護;保護配合;選擇性;定值優化;粒子群算法
0 引言
現代電網飛速發展與高度復雜,傳統定時限過流保護由于受運行方式等因素影響,其整定配合難度急劇增加,容易造成失配以致保護越級動作,難以滿足電網安全穩定運行需求。而在原理上具備緊密反映短路電流變化特征優勢的反時限過流保護,與很多負載的故障特性相近,選擇性與速動性易同時滿足。國外電力系統普遍將其作為輸電網后備保護及配網主保護[1],在我國電網的應用則處于逐步增加的狀態[2]。
相較于階躍式定時限保護,具有一定弧度的反時限保護動作曲線存在整定配合困難等缺點[3],極大限制了其應用。因此,目前國內反時限保護多用于配合關系較少的單元件保護(如發電機[4]、電動機等)、微網保護[5-6]、配網保護[7-8]及微機保護反時限算法研究[9];涉及元件之間配合,則文獻研究甚少[10-12],工程中則常采取簡化方法,比如忽略彼此配合,統一取固定值,既嚴重削弱了反時限保護的優勢,亦存在不嚴格配合帶來的隱患與風險。
鑒于此,本文以反時限過流保護選擇性與快速性為核心,建立了反時限過流保護之間配合、反時限與定時限保護配合的整定原則,并定義了整定范圍內的時間優化目標,將優化算法融入整定計算軟件,得到滿足工程需要的保護定值。
1 反時限過流保護曲線特性
保護動作時間隨故障電流的增加而減小是反時限過流保護的基本特征,學術界、工程界通常將反時限動作時間-故障電流特性曲線擬合,得到其通用動作方程:
(1)
式中:TDS(Time Dial Setting, TDS)為時間系數(0.05~1.1);t為保護動作時限;Ik為流過保護處的短路電流;Iop(Pickup Current Setting)為動作電流,整定時要求滿足下式:
(2)
式中:IL.max和Ik.min分別為最大負荷電流和最小短路電流。K1~3為曲線常數,本文以電網常采用的一般反時限曲線(K1=0.14,K2=0.02,K3=-1)且線路元件配合為例進行研究。
2 反時限過流保護選擇性分析
線路反時限過流保護選擇性體現為本元件后備保護時間比相鄰元件保護時間留有足夠裕度,即在保護范圍內電流-時間動作曲線上兩曲線沒有交集。以圖1所示系統為例,保護R1與R2配合特性曲線如圖2所示[13],動作時間分別為t1與t2,見式(1)。選擇性滿足要求,即要求在保護范圍內下式成立[14]:
(3)
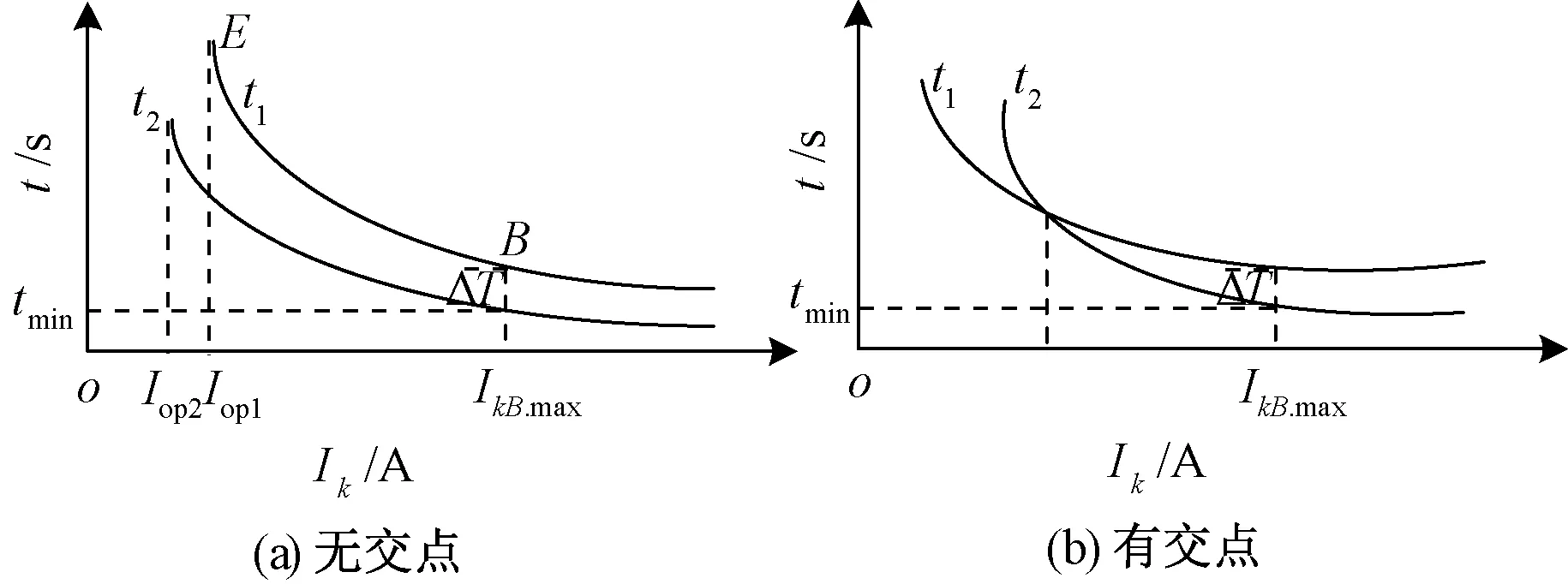
圖2 保護配合特性曲線

圖1拓撲圖
下面分別分析線路反時限過流保護之間配合及與定時限保護之間配合情況。
2.1線路反時限過流保護之間配合
圖1所示系統中保護R1與R2均為一般反時限,其配合特性曲線如圖2所示。R1曲線方程可通過點E、B兩點確定,見圖2(a)。點E確定啟動電流Iop1,點B則意味著圖1中母線B故障時t1-t2≥ΔT,時間級差ΔT常取0.3 s。而對于母線C故障時,t1與t2大小關系則存在圖2(a)、(b)兩種情況。若為后者,則意味著線路BC發生故障時,保護R1有可能誤動作。
將t1與t2用式(1)表征后代入式(3),則滿足式(3)等價于滿足:
y=kx-b>0
(4)
式中:
b=TDS1-TDS2
式中:Ik為線路BC故障流過保護R2的電流;Kfz保護R1對R2的分支系數。
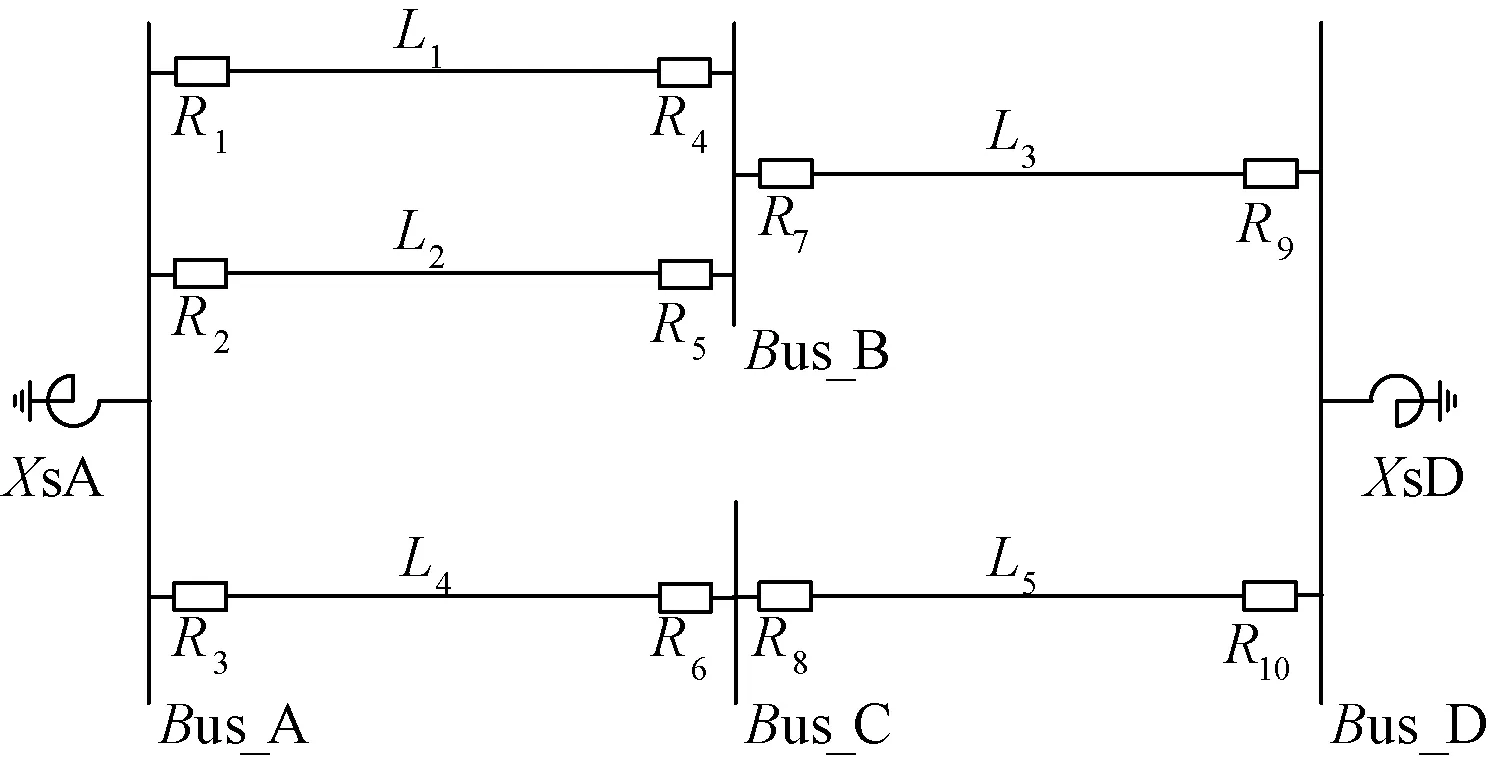
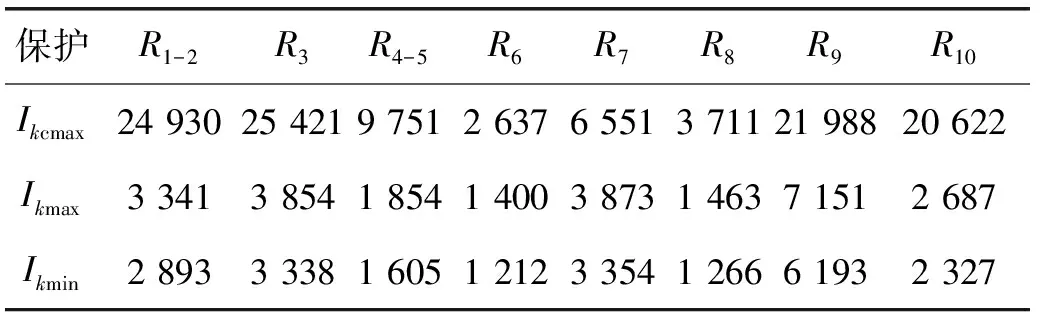
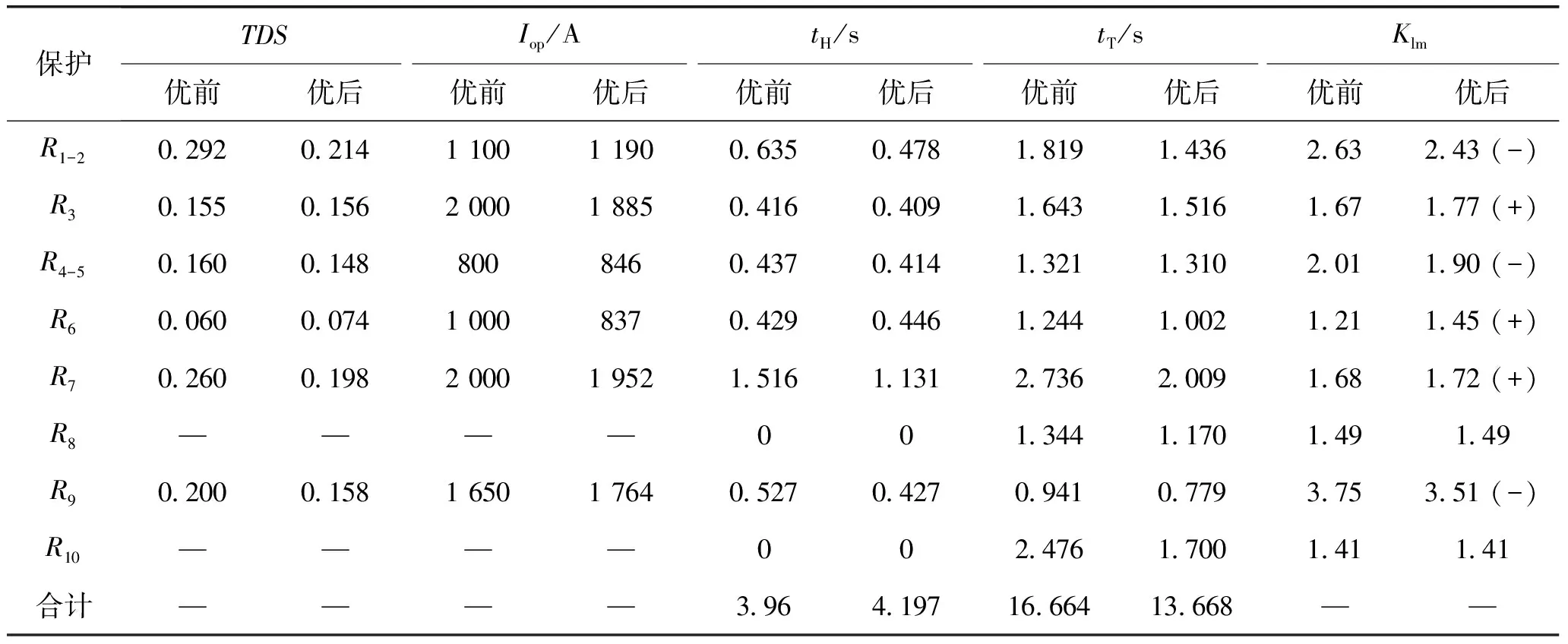
式(4)為一元一次函數,當斜率k<0時,理論上存在故障電流數值很大的情況下,y<0,較難滿足選擇性要求,因此令k>0易于定值整定。
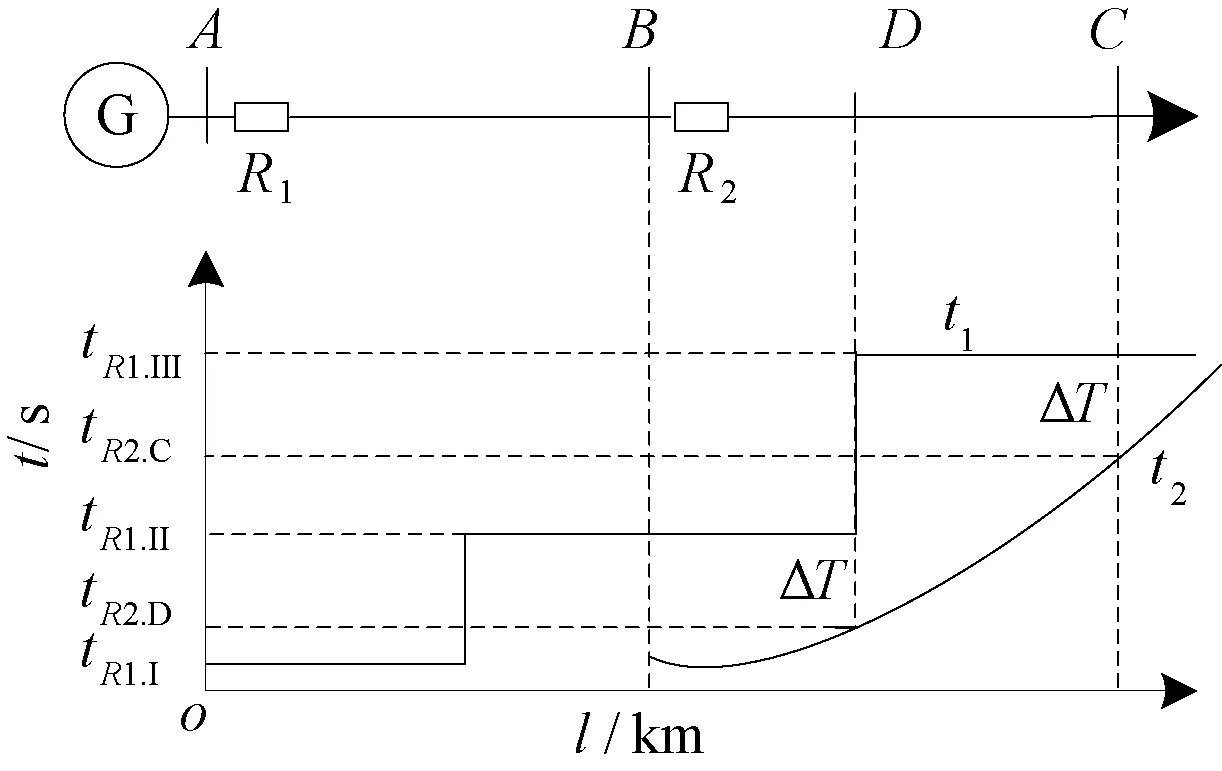
若記Iop_max=max{Iop1/Kfz,Iop2},則只需在Iop_max點滿足式(4),加上k>0則保證了線路BC任一點故障均滿足了選擇性。將Iop1/Kfz>Iop2與Iop1/Kfz 考慮必須保證R2出口(近似B處)故障時滿足ΔtB≥ΔT。 因此,保護R1與R2配合滿足選擇性,即達到圖2(a)所示,必須滿足下式: (5) 實際整定過程中,Kfz取為最大分支系數。 2.2線路反時限過流保護與定時限保護配合 如圖3,保護R1為反時限過流保護,R2為定時限過流保護或距離保護(R2整定原則依照現有規程,本文略);由于R2Ⅱ段保護范圍已經伸出該線,故本文僅分析R1與R2兩段配合時情況。D處為R2Ⅰ段定值對應的保護范圍末端,記在B,D處R1動作時間t1分別為tR1,B、tR1,D,R2的Ⅰ段、Ⅱ段動作時間分別為tR2,I(≈0 s)和tR2.II。保護R1與R2配合滿足選擇性,必須滿足下式: (6) 整定過程中,難點在于確定D位置,若R2為距離保護,則D位置較為固定,距離B約占全線70%~80%;若R2為定時限過流保護,大方式下D處偏離B,小方式下D處偏向B。考慮到傳統整定軟件在配合時簡單將故障點設置在母線C處的做法,建議參照部分整定軟件已擴展了提供線路中點(記為M處)故障計算結果的做法。 圖3 反時限保護與定時限保護配合 實際應用中,可參照如下步驟在整定軟件中完成整定原則代碼: (1) 若線路BC配有全線速動保護(如差動保護、縱聯保護或其他帶極短延時全線保護),時間為tR2.ZL,則整定只需滿足式(7)即可,否則執行(2)。 (7) (2) 若由于線路BC太短或大小方式差異太大導致R2Ⅰ段無足夠保護范圍而退出,則只需滿足式(8),否則執行(3)。 (8) (3) 鑒于式(8)為式(6)的一種特例,故直接用式(8)進行計算。若不滿足配合或配合困難,則執行(4)。 (4) 用式(6)進行計算,若R2為距離保護,則D取M處進行計算;若R2為定時限過流保護,大小方式均參與,若R2Ⅰ段D處偏向C,則D取M處;若偏向B,則D取B處參與計算。 2.3線路定時限保護與反時限過流保護配合 如圖4,R1為定時限保護,R2為反時限保護,動作時間分別為t1和t2。R1在Ⅱ段保護范圍末端D處時間為tR1.II,R2該處時間為tR2.D。對于R1遠后備Ⅲ段僅考慮C處配合已足夠,時間分別為tR1.III、tR2.C。 由圖可知,保護R1與R2配合滿足選擇性必須滿足下式: (9) 與上節類似,難點在于確定D位置,若R1為距離保護,則D位置較為固定,距離B約占AB線120%~130%;若R1為定時限過流保護,建議Ⅱ段電流定值按保本線末端(B處)故障有靈敏度整定,Ⅲ段定值按躲最大負荷電流整定。 圖4 定時限保護與反時限保護配合 在實際應用中,可參照如下步驟在整定軟件中完成整定原則代碼實現: (1) 若由于線路BC太短或大小方式差異太大導致R1Ⅱ段伸出C處,則只需滿足式(10),否則執行(2)。 (10) (2) 鑒于式(10)為式(9)的一種更苛刻情形,故直接用式(10)進行計算。若不滿足配合或配合困難,則執行(3)。 (3) 用式(9)進行計算,若R1為距離保護,則D取線路BC中點M處進行計算;若R2為定時限過流保護,大小方式均參與,若由R1Ⅱ段D處偏向B,則D取M處;若偏向C,則取式(10)參與計算。 (4) 若簡化處理,可將tR1.III固定取為比tR1.II增加一個延時。 對于其他元件間保護配合(如變壓器反時限過流保護與出線距離或定時限保護配合),均可參照本節所述原則進行整定。 3.1快速性及優化目標 選擇性配合原則融入整定軟件進行整定計算雖然提高了實踐可操作性,但與傳統整定配合一樣具有僅考慮相鄰一或二級的不足,計算出來的結果滿足配合,但是從全網范圍來看,動作時間可能會比較長,影響了全網保護動作的“快速性”。 因此,有必要對其予以優化。將考察對象組成一個集合,以集合總的保護動作時間最短為優化目標,其函數為: (11) 式中:n為集合內元件數,常取為待整定元件數;wi為權重系數,與線路的重要程度成正比,以保證其及周邊元件嚴格完全配合;tRi為保護Ri的動作時間。 3.2曲線參數約束條件 鑒于反時限過流保護的曲線特性,其動作方程中各參數均應考慮其限值,優化計算中必須滿足式(2)及下式: (12) (13) 式中:tmin為斷路器固有時間,常取0.02 s。 3.3選擇性配合約束條件 將上節所述選擇性分析作為保護配合的約束條件,具體為。 (1) 若上下級保護均為一般反時限,則取式(5)為約束條件。 (2) 若為反時限與定時限保護配合,則取式(6)-(8)及衍生邏輯步驟作為約束條件。 (3) 若為定時限與反時限保護配合,則取式(9)-(10)及衍生邏輯步驟作為約束條件。 3.4優化算法 本文采用在優化領域具有一定優勢的粒子群優化算法[15](PSO)對保護定值進行優化。該算法中,每個粒子代表D維空間的一個潛在可行解,以一定速度飛行,并根據自身歷史最優位置與群體歷史最優位置進行動態調整。第i個粒子當前位置與速度分別記為Xi=(xi1,xi2,…,xiD)與vi=(vi1,vi2,…,viD),該粒子自身歷史最優位置與群體歷史最優位置分別記為Pi=(pi1,pi2,…,piD)與Pg=(pg1,pg2,…,pgD)。鑒于壓縮因子K有助于保證PSO算法收斂,且不需使用最大速度(vmax)[16-17],故本文采用壓縮因子粒子群算法(K-PSO),具體方程為: (14) 為驗證本文所述方法的正確性及可行性,以圖5所示某220 kV電網局部區域進行保護整定計算及定值優化,具體參數(標幺值)見表1,其中X1為正序電抗,Xs表示外部電網等值電抗。短路電流見表2,其中Ikcmax、Ikmax及Ikmin分別為保護正向出口故障流過保護最大短路電流、保護所在線末故障流過保護最大及最小短路電流。保護R8與R10為定時限保護(電流定值依據現有規程整定),其余為帶方向反時限保護;式(2)中最大負荷電流IL.max取700 A,式(11)中權重系數wi取1。 圖5 電力系統拓撲 名稱XsAXsDL1(L2)L3L4L5X1000930011400562002390056000817 表2 短路電流 A 計算詳細結果見表3,其中tH、tT分別為保護正向出口故障、保護所在線末故障時的保護動作時間。采用前述保護配合整定原則計算得到定值見表3“優前”,滿足了保護配合的選擇性要求;在其基礎上融入粒子群優化算法進行優化。初始種群數設為100,優化目標為式(11),約束條件見3.2與3.3節,進行優化計算后得到一組可行定值解見表3“優后”。考慮到tT對保護時間影響更大,故式(11)中tRi取為tT。對比可知優化前,時間總和∑(tH+tT)=20.624 s;優化后:∑(tH+tT)=17.865 s。盡管優化后tH稍有增加(6%),但tT下降幅度更大(18%),整體動作時間降低2.759 s(降幅13%)。靈敏性方面,Klm為保護在本線路末端故障時的靈敏度;(+)、(-)分別表示優化前后靈敏系數提高和降低。通過計算Klm可知,雖然保護靈敏度各有提高(R3、R6、R7)與降低(R1、R2、R4、R5、R9),但是前者優化前靈敏度較低(最低值為1.21),已接近規程要求的下限,故優化后對前者靈敏度的提高具有更重要的意義。因此,本算例驗證了本文所述方法在滿足選擇性并兼顧靈敏性的同時提升了全網保護快速性的目標。 表3 整定及優化結果 分析整定配合過程及優化計算可發現,本文所述方法的優勢在于:①明確提出了反時限保護與其他定時限保護整定配合原則,一旦將其融入整定計算軟件實現自動整定,便可彌補目前手工計算或簡化處理反時限保護的短板;②整定計算過程計及優化算法后,則整體動作時間降低,在滿足選擇性的同時提升了快速性。 本文從保護選擇性角度詳盡地分析反時限保護之間配合、反時限與定時限保護配合的整定原則,在其基礎上從快速性角度建立了優化模型,并以算例進行了相應測試與驗證。鑒于目前利用整定軟件實現反時限保護自動整定鮮有報道,故在以下方面可進一步開展深入研究:本文僅分析常見的反時限與其他保護配合原則,未計及特殊情況的處理,如T接線、串補線等;本文僅部分利用整定軟件,完全實現整定軟件自動整定,則需與軟件廠家密切配合,深入研究;優化算法融入整定軟件,則需進一步完善算法本身及軟件接口交互處理等。 [1]ABDELAZIZ A Y, TALAAT H E A, NOSSEIR A I, et al. An adaptive protection scheme for optimal coordination of overcurrent relays[J]. Electric Power Systems Research, 2002, 61(1): 1-9. [2]陶冶,田鵬飛. 遼寧電網零序電流反時限保護速動性分析[J]. 東北電力技術, 2012,33(12): 34-36. [3]張全有. 電動機反時限過流保護模型的分析與算法實現[J].安徽工程大學學報, 2014,29(3): 65-67. [4]王育學,尹項根. 基于能力曲線最優擬合的大型發電機反時限保護研究[J].廣東電力, 2014,27(11): 71-76. [5]黃文燾,邰能靈,楊霞. 微網反時限低阻抗保護方案[J]. 中國電機工程學報, 2014, 34(1): 105-114. [6]許偲軒,陸于平,王業. 基于邊電壓的反時限微網保護方案[J].電力系統自動化, 2014,38(1):68-73. [7]郭煜華,姜軍,范春菊,等. 改進的配電網反時限過電流保護[J].電力自動化設備, 2015,35(10):45-50. [8]劉玉,李季英. 含分布式電源配電網的改進反時限過電流保護算法[J].吉林電力, 2014,42(5):12-15. [9]顧志飛,江衛良,郝后堂,等. 一種微機型反時限過激磁保護的實現方法[J].電力自動化設備, 2012,32(7):149-153. [10]吳麟琳,黃少鋒.平行雙回線對反時限零序電流保護的影響及改進算法[J].電網技術, 2013,37(3): 707-712. [11]韋嘉,柏瑜,熊蘭,等. 反時限過流保護模型優化與曲線交叉研究[J]. 電測與儀表, 2015,52(9): 56-60,63. [12]趙黎麗,高昌培,林虎.線路和變壓器零序反時限保護及其整定配合[J].電力系統自動化, 2011,35(17):107-110. [13]黃超. 計及風險的繼電保護在線校核研究[D]. 武漢:華中科技大學, 2012. [14]侯計兵. 電力系統反時限過流保護優化整定計算研究[D]. 武漢:華中科技大學, 2011. [15]劉順桂,朱正國,丁慶. 基于粒子群算法的微網保護裝置位置優化[J]. 電力系統及其自動化學報, 2015,27(S1): 54-58. [16]張成興. 壓縮因子綜合信息粒子群算法[J]. 計算機科學與探索, 2014,8(4): 506-512. [17]王曉佳,張寶霆,徐達宇. 含有壓縮因子的粒子群優化灰色模型在智能電網中的應用[J]. 運籌與管理, 2012,21(3): 114-118. Research on Optimal Coordination of Inverse-time Overcurrent Protection HUANG Chao, YANG Yan, TIAN Junyang (Guangxi Electric Power Dispatching and Control Center, Nanning 530023, China) The inherent advantage of the inverse-time overcurrent protection which can closely reflect the change of the short-circuit current is concealed due to the difficulties of the curve coordination, so its application is limited to some extent. Therefore, on the basis of thorough analysis with the strict coordination between protection curves, the setting principles of the coordination between inverse-time overcurrent protection and definite-time protection are presented in this paper with the selectivity of protection being taken into account. And using particle swarm optimization algorithm with constriction factor(K-PSO) accompanied by constraint conditions, such as the curve parameters and selective cooperation, the time-optimization target based on the calculation range of protection setting is built from the perspective of rapidity under the premise of high sensitivity. The setting principles and optimization model can be used for protection setting calculation and setting optimization of inverse-time overcurrent protection respectively, which is helpful for improving the domestic practical value for engineering application. The validity and feasibility of this method are verified through the example. inverse-time overcurrent protection; protection coordination; selectivity; setting optimization; particle swarm optimization algorithm 2016-06-04。 黃超(1987-),男,工程師,研究方向為電力系統繼電保護整定計算及定值優化,E-mail:huang_c.dd@gx.csg.cn。 TM771 ADOI:10.3969/j.issn.1672-0792.2016.10.003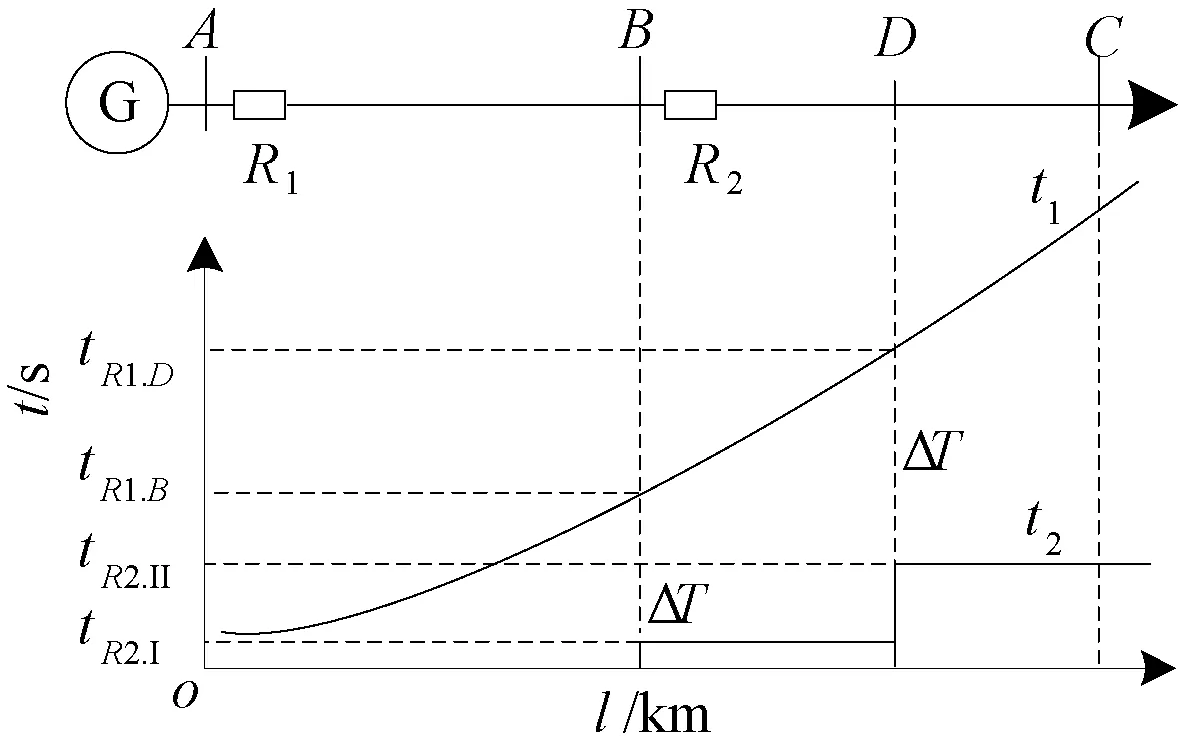
3 反時限過流保護快速性分析及優化模型
4 算例

5 結論

