基于滑模觀測器的無軸承永磁同步電機無速度傳感器矢量控制*

陶 濤， 唐明軍， 花良浩， 周 杰， 呂志香

(揚州工業職業技術學院 電氣與信息工程學院，江蘇 揚州 225127)

?

基于滑模觀測器的無軸承永磁同步電機無速度傳感器矢量控制*

陶 濤， 唐明軍， 花良浩， 周 杰， 呂志香

(揚州工業職業技術學院 電氣與信息工程學院，江蘇 揚州 225127)

為解決無軸承永磁同步電機矢量控制系統中傳統機械式傳感器帶來的成本及可靠性等問題，將滑模觀測器技術應用到其控制系統中。該系統采用滑模面及滑模等效控制方法，并基于轉矩繞組觀測電流和其實測電流差值構建滑模面，觀測電機反電動勢，從而實現轉子位置角及轉速的精確估算。利用MATLAB仿真軟件構建了無速度傳感器運行仿真系統，對電機轉速、轉角信號進行辨識。仿真結果表明： 滑模觀測器的轉角、轉速信號辨識精度較高，并能滿足無軸承永磁同步電機無速度傳感方式的穩定懸浮運行要求。

無軸承永磁同步電機； 滑模觀測器； 速度自檢測； 轉角自檢測

0 引 言

無軸承永磁同步電機(Bearingless Permanent Magnet Synchronous Motor, BPMSM)是一種結合了磁懸浮技術并集永磁同步電機優良特性于一體的新型電機。因此，其既具有永磁同步電機固有特征： 高功率、高能量密度、高功率因數；同時兼具磁懸浮軸承優異性能： 無摩擦、無需潤滑、免維護、壽命長。因此，其可實現高速及超高速運行，是高速電機傳動領域里的一項重大突破[1-2]。

基于轉子磁場定向的解耦算法可實現徑向懸浮力和轉矩的獨立控制，轉子磁場定向控制需要能獲得精確的轉角、轉速信號，從而獲得磁場定向所需磁通的位置，進而實現轉矩和徑向懸浮力解耦控制，最終滿足BPMSM穩定懸浮運行要求。傳統BPMSM矢量控制系統中位置/轉速信號均采用機械式傳感器測量，而機械式傳感器的安裝與使用不僅使電機體積、成本增加，可靠性降低，更嚴重限制了BPMSM高速優良性能的發揮。因此，BPMSM無速度傳感器技術因其具有重要的現實意義和廣闊的應用前景，從而成為當前及未來的研究熱點[3-6]。

國內外學者針對電機無速度傳感技術提出了很多控制方法，大體可以分為三類[7-12]： 一類是基于電機理想模型的開環計算方法，如直接計算法、基于電感變化的估算法及反電動勢積分法等，這類方法計算過程簡單，在電機參數正確的前提下能夠得到較為準確的轉子位置估算結果，開環計算的方法原理簡單，動態響應較快，但是這類方法極易受參數變化影響，算法不穩定。另一類是基于各種觀測器模型的閉環算法，當前應用較為廣泛的有擴展卡爾曼濾波器、滑模觀測器、模型參考自適應算法及其他自適應算法等，電機無速度傳感器控制在速度觀測精度和系統的穩定性上都有了很大的提高。最后一類是以高頻注入法為典型代表的基于電機非理想特性的算法，利用凸極機自身的凸極特性或者在高頻信號下隱極機所表現出來的凸極特性，來估算電機轉子位置和轉速，為無位置傳感器在極低速下的應用提供了新的思路。

本文通過借鑒傳統永磁電機無速度傳感器檢測方法，提出基于滑模觀測器的BPMSM無速度傳感器矢量控制系統。通過在轉矩繞組觀測電流和其實測電流的誤差上構建滑模面，觀測電機反電動勢，從而實現轉子位置角及轉速的精確估算。仿真結果表明： 滑模觀測器的轉角、轉速信號辨識精度較高，并能滿足BPMSM無速度傳感方式的穩定懸浮運行要求。

1 BPMSM數學模型

BPMSM徑向懸浮力產生的實質是由于懸浮力繞組所產生的磁場打破了原有轉矩繞組所建立的氣隙磁場平衡，從而產生作用在轉子表面的徑向懸浮力。將轉矩繞組極對數數值大小設為pM，懸浮力繞組極對數數值大小設為pB，理論分析與試驗結果均有力地證明了無軸承電機若需實現正常運行和穩定懸浮功能，必須滿足以下三個條件，缺一不可： (1)pB=pM±1；(2) 兩磁場旋轉方向相同；(3) 產生旋轉磁場的電流電角頻率一致。

為了更為清晰地描述本文所建立的數學模型，現定義相關參數變量。定義ψM、ψB、ψPM分別為轉矩繞組磁鏈、懸浮力繞組磁鏈、轉子永磁體產生的磁鏈，ψMd、ψMq、ψBd、ψBq為相應繞組磁鏈直軸、交軸分量；iM、iB分別為轉矩繞組電流、懸浮力繞組電流，iMd、iMq、iBd、iBq為相應繞組電流在直軸、交軸上的分量。

當轉矩繞組極對數pM與懸浮力繞組極對數pB均≥2且滿足pB=pM±1時，轉矩繞組磁鏈ψM與懸浮力繞組磁鏈ψB之間沒有相互交鏈。由于本文采用的是表貼式BPMSM，對于轉矩繞組，有LMd=LMq=LM；對于懸浮力繞組，有LBd=LBq=LB。因此，當轉矩繞組極對數pM與懸浮力繞組極對數pB均≥2且滿足pB=pM±1時，BPMSM的轉矩繞組與懸浮力繞組磁鏈方程分別為

(1)

(2)

當電機穩定運行，且轉子穩定懸浮時，轉矩繞組與懸浮力繞組電壓方程分別為

(3)

(4)

式中：RM——兩相旋轉坐標系下的轉矩繞組電阻；

RB——兩相旋轉坐標系下的懸浮力繞組電阻；

ω——同步旋轉機械角速度。

對于表貼式BPMSM，當轉子處于中心位置時，BPMSM的電磁轉矩表達式應與普通永磁同步電機的電磁轉矩表達式一致，即：

(5)

BPMSM轉子受到的徑向力包括三部分： 轉子在電機氣隙磁場中受到的麥克斯韋力構成的徑向力；載流轉矩繞組在懸浮力繞組氣隙磁場中受到的洛侖茲力，與載流懸浮力繞組在轉矩繞組氣隙磁場中受到的洛侖茲力的作用于轉子的反作用力構成的徑向力；由于轉子偏心引起氣隙磁場分布不均而產生的徑向力。所以BPMSM的徑向懸浮力為

(6)

式中：km、kc、kq——常數；

IPM——轉子永磁體激勵的磁場等效至轉矩繞組中的電流部分。

2 滑模觀測器的設計

本文研究的對象是轉矩繞組極對數pM=2、懸浮力繞組極對數pB=3的表貼式BPMSM。其轉矩控制模塊在靜止兩相坐標系α-β下的數學模型為

(7)

其中：A=(-RM/LM)·I

B=(1/LM)·I

式中：iM——轉矩繞組α、β軸電流，iM=(iα，iβ)T；

uM——轉矩繞組α、β軸電壓，uM=(uα，uβ)T；

EM——轉矩繞組α、β軸反電動勢，EM=(Eα，Eβ)T；

RM——轉矩繞組電阻；

LM——轉矩繞組電感。

可定義滑模面S為

(8)

電流的滑模觀測器為

(9)

且

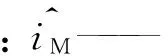
h——滑模增益；

sgn——符號函數。

式(9)減去式(7)得轉矩繞組電流觀測誤差的狀態方程為

(10)

如果滿足式(11)所示的滑模條件，則系統進入滑模狀態：

(11)

滑模增益h必須足夠大才能滿足到達滑模狀態的條件，但若其值過分大將會引起抖振噪聲，從而導致估計誤差，因此選擇合適的滑模增益是問題的關鍵。取正定Lyapunov函數：

(12)

其中：

(13)

(14)

取滑模增益為

(15)

式中：δ——正常數。

A1，A2均小于0，從而使得U<0，滿足滑模條件式(11)，進而系統得以進入滑模狀態。此時，有

(16)

將式(16)代入式(10)，可得

EM=K

(17)

將不連續的含有高頻成分的切換控制量經過適當的低通濾波器后得到等價控制量，即估算反電勢：

(18)

(19)

根據式(12)、式(13)可計算求得轉子位置角：

(20)

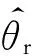
3 BPMSM無速度傳感器控制系統仿真研究

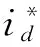
浮力繞組極對數pB=3，永磁體勵磁磁通ΨPM=0.175Wb，轉矩繞組電阻RM=2.875Ω，轉矩繞組電感LMd=LMq=LM=8.5mH，給定轉速n*=8000r/min。

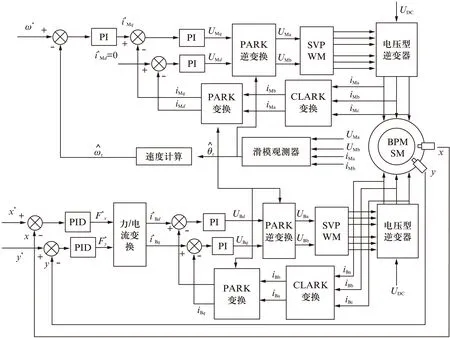
圖1 基于滑模觀測器的BPMSM無傳感器矢量控制系統框圖

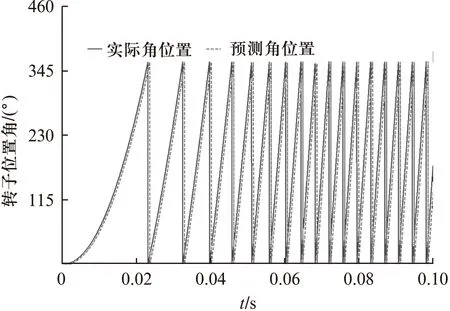
圖2 8000r/min轉速下轉子位置實測值與估計

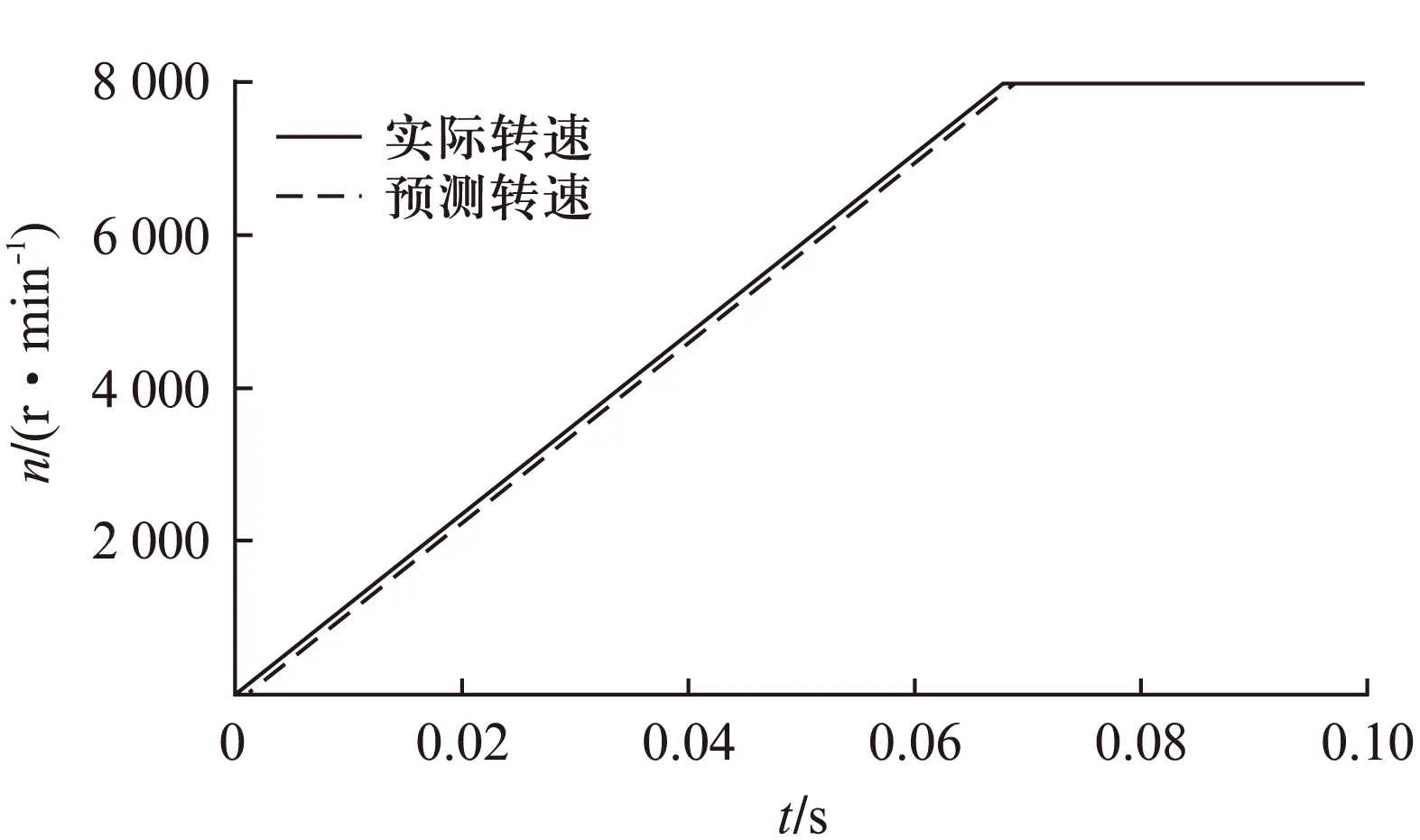
圖3 轉速實測值與估算值

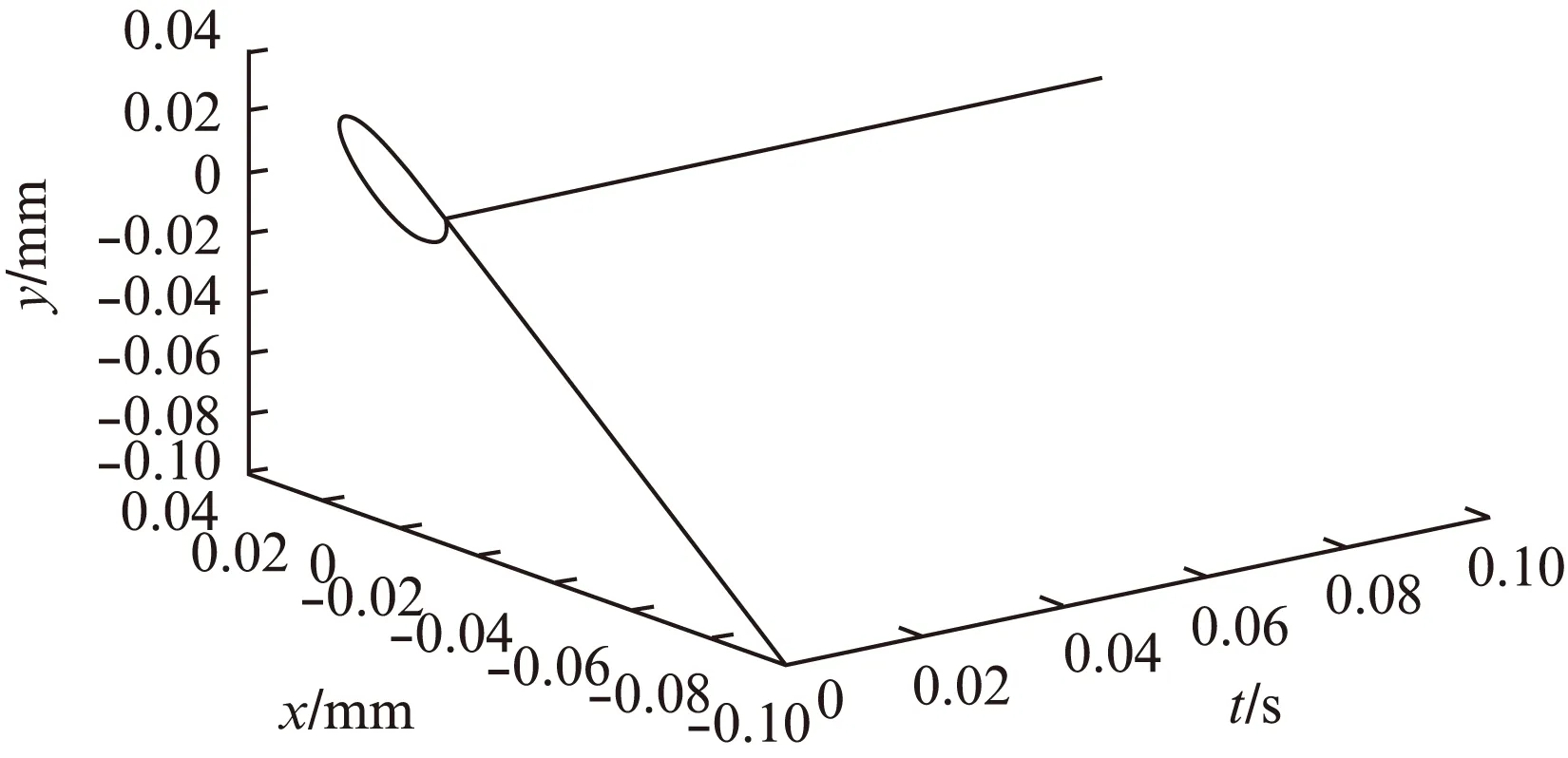
圖4 轉子起伏波形圖

4 結 語

本文采用滑模面及滑模等效控制方法，并基于轉矩繞組觀測電流和其實測電流差值構建滑模面，觀測電機反電動勢，從而實現轉子位置角及轉速的精確估算。利用MATLAB仿真軟件構建了無速度傳感器運行仿真系統，對電機轉速、轉角信號進行辨識。仿真結果表明： 滑模觀測器的轉角、轉速信號辨識精度較高，并能滿足BPMSM無速度傳感方式的穩定懸浮運行要求，為今后搭建BPMSM無速度傳感試驗平臺奠定了理論基礎。

[1] THOMAS N, PHILIPP K, FRANZ Z, et al. Magnetically levitated slice motors-an overview[J]. IEEE Transactions on Industrial Applications， 2011, 47(2)： 754-766.

[2] 年珩，賀益康，黃雷.內插式永磁無軸承電機轉子位置/位移綜合自檢測[J].中國電機工程學報，2007，27(9)： 53-58.

[3] 周令康，曹莉，王毅，等.基于高頻注入法的無軸承同步磁阻電機無速度傳感器研究[J].微電機，2012，45(10)： 43- 47.

[4] 朱熀秋，陳朝亮，鄧建明，等.無軸承永磁同步電機無速度傳感器控制系統[J].電機與控制應用，2008，35(5)： 18-22.

[5] 黃雷，崔迎.基于滑模觀測器的永磁同步電機無傳感器矢量控制[J].機電工程，2012，29(11)： 1303-1305.

[6] 陳坤華，孫玉坤，吳建兵，等.基于電感模型的開關磁阻電機無位置傳感技術[J].電工技術學報，2006，21(11)： 71-75.

[7] BOSE B K. Modern power electronics and AC drives[M]. Beijing： Pearson Eduation North Asia Limited and China Mechine Press, 2002.

[8] CHEN Z Q, TOMITA M, ICHIKAWA S, et al. Sensorless control of interior permanent magnetic synchronous motor by estimation of an extended electromotive force[C]∥IEEE Industry Applocations Conferences, 2000： 1814-1819.

[9] 張猛. 無機械傳感器永磁同步電機控制及磁鏈觀測[D]. 北京： 清華大學, 2007.

[10] WANG L M, LORENZ R D. Rotor position estimation for permanent magnet synchronous motor using saliency-tracking self-sensing method[C]∥Proc of IEEE-IAS 2000 Annual Meeting, Rome, Italy, 2000： 445- 450.

[11] 李永東，朱昊.永磁同步電機無速度傳感器控制綜述[J].電氣傳動，2009,39(9)： 445- 450.

[12] LI H R, WANG J H, GU S S, et al. A Neural-network-based adaptive estimator of rotor position and speed for permanent magnet synchronous motor[C]∥IEEE ICEMS， 2001： 735-738.

Seneorless Vector Control of Bearingless Permanent Magnet Synchronous Motor Based on Sliding Mode Observer*

TAOTao，TANGMingjun,HUALianghao,ZHOUJie,LVZhixiang

(Department of Electronic and Electrical Engineering, Yangzhou Polytechnic Institute, Yangzhou 225127, China)

A novel control strategy based on sliding mode observer was present for the purpose of solving the problems of cost and reliability caused by the mechanical sensor of the bearingless permanent magnet synchronous motor (BPMSM) vector control system. The sliding-mode surface and the sliding-mode equivalent control method was used in the control system. And, the sliding-mode surface was defined on the errors between the actual and estimated currents. The estimated back-EMF was observed to calculate the angle and speed of the rotor. Simulation system of speed sensorless was constructed in MATLAB/Simulink environment and simulations of speed/angle identification for the rotor were carried out. The simulation results had showed that sliding mode observer speed/angle identification precision was very well and was able to achieve stable sensorless suspension running.

bearingless permanent magnet synchronous motor (BPMSM)； sliding mode observer； self-sensing for rotor speed； self-sensing for rotor angle

江蘇省大學生實踐創新訓練計劃(201513754005Y);揚州市重點研發項目(YZ2015084)

陶 濤(1988—)，男，碩士研究生，講師，研究方向為無軸承電機智能控制技術。

TM 351

A

1673-6540(2016)10-0009-05

2016-06-18