具有Markovian調制的隨機資本系統數值解的收斂性

鄭來運

(寧夏大學 機械工程學院， 銀川 750021)

?

具有Markovian調制的隨機資本系統數值解的收斂性

鄭來運

(寧夏大學 機械工程學院， 銀川 750021)

根據Euler數值方法，給出了一類具有Markovian調制的役齡相關隨機資本系統的數值解，并應用It公式、Burkholder-Davis-Gundy不等式和Gronwall引理證明了數值解的收斂性，給出了數值解收斂于解析解的充分條件。

隨機資本系統；Markovian調制；It公式

考慮如下具有Markovian調制的役齡相關隨機資本系統：

(1)

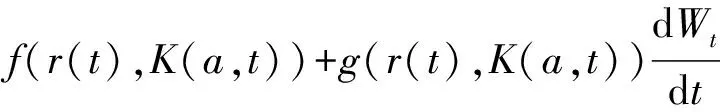
帶Markovian調制的系統具有很好的優點，它能描述(模型化)動力系統中結構的突然變化，如系統組成部分的失敗或修復、突然的環境變化、子系統間互聯的改變以及對不同的非線性部分的操作等[1]，因此受到了廣泛關注[2-17]。由于一般很難或無法獲得該系統的解析解，近年來，很多學者更加關注隨機微分方程數值解的研究。例如：Yuan等[2]討論了具有Markovian調制的隨機微分方程 數值解的收斂性；Wang等[5]研究了帶 Poisson 跳和 Markovian調制的隨機時滯微分方程數值解的收斂性；Rathinasamy等[6]給出了帶多時滯和Markovian調制的線性隨機微分方程半隱式Euler法的均方穩定性，最近又討論了具有Markovian調制的年齡相關隨機種群系統分裂步數值方法[7]；Zhou等[8]證明了在局部 Lipschitz 條件下，帶 Markovian調制的中立型時滯隨機微分方程數值解的收斂性；Li等[9]討論了帶Markovian調制的隨機時滯微分方程數值解的收斂性和穩定性，并研究了帶Markovian調制[10]以及帶跳和Markovian調制[11]的年齡相關隨機種群方程數值解的收斂性；Jiang等[12]討論了帶Markovian調制的隨機時滯積分微分方程分裂步向后Euler數值解的穩定性；張啟敏等[13-14]研究了帶Markovian調制的年齡相關隨機種群系統數值解的漸漸穩定性以及半馴服Euler法的指數穩定性。對于投資模型問題，Markovian調制模型在金融經濟學的多個重要領域均有應用[15-16]，但對于帶Markovian調制的役齡相關隨機資本系統，相關研究較少[17]。本文討論給定條件下帶Markovian調制的役齡相關隨機資本系統數值逼近解的收斂性。

1　預備知識和Euler逼近

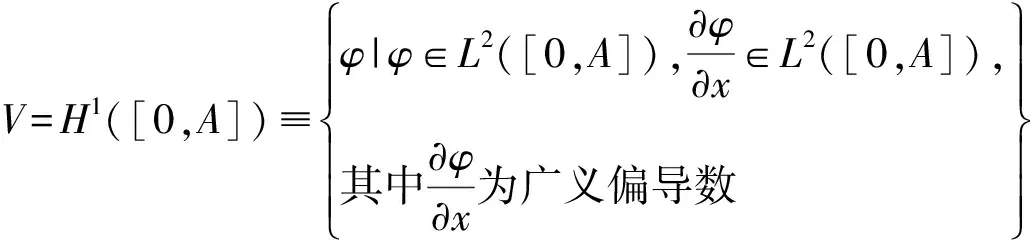
設(Ω,F,P)是一個完備概率空間，{Ft}t≥0是其上的一個濾子且滿足一般性條件(即單調增右連續，且F0包含所有的P零測集)。設r(t),t>0為定義在(Ω,F,P)上取值于有限狀態S={1,2,…,N}的右連續Markovian鏈，其生成元Γ=(γij)N×N定義如下：

其中，Δ>0，γij≥0(i≠j)表示從狀態i到狀態j的轉移概率，且

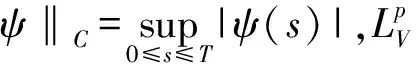
(2)

其中，Kt=K(a,t)。

對于系統(1)，取Δt=h為離散時間步長(時間增量)，則其Euler逼近解迭代式為

(3)

初始值

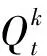
(4)

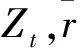
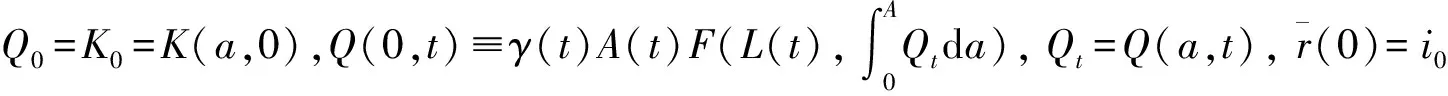
假定系統(1)滿足如下條件：

1)μ(a,t)在Q上非負可測，γ(t)和A(t)在[0;T]上非負連續，滿足

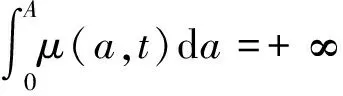
2)f(i,0)=0,g(i,0)=0,i∈S。

3) (Lipschitz條件)存在正常數Ki，對任意x,y∈H,i∈S，有

若上述條件成立，則方程(1)在(a,t)∈Q上存在唯一解K(a,t)，證明方法與文獻[18]中方法類似，這里不再贅述。

2　相關引理

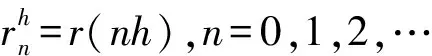
引理2若條件(A)-(D)成立，則存在常數k≥2和C1>0，使得

證明過程類似于文獻[17]，且可得

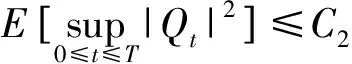
證明由式(4)可得

對|Qt|2應用It公式，有

于是得

對?t∈[0,T]，有

利用條件3)得

基于QoS綜合匹配的語義Web服務選擇方法過程中，兩個QoS屬性參數之間相關性的臨界距離L，本文將其設定為1。QoS語義匹配成功后，對相應的QoS數值進行匹配。

(5)

應用Burkholder-Davis-Gundy不等式，對某些正常數M1>0，有

(6)

于是由式(5)和(6)可得

應用 Gronwall 引理，得

證明完畢。

引理4對任意的t∈[0,T]，存在正常數C3和C4，使得

引理5若條件1)～3)成立，則存在常數C5使

證明對任意的t∈[0,T]，存在正整數m，使得t∈[mh,(m+1)h)，有

于是，

應用Cauchy-Schwarz不等式和假設條件，有

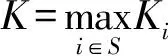
應用Doob不等式和引理3，有

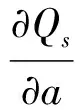
證明完畢。

3　數值解的收斂性

由引理1～5可證明在給定條件1)～4)下，具有Markovian調制的役齡相關隨機資本系統的數值解收斂到其解析解。

定理1若條件1)～4)成立，則

證明由式(2)和(4)，有

于是，對?t∈[0,T]，有

應用Burkholder-Davis-Gundy不等式，得

其中，k1和k2均為正常數。于是有

再利用Gronwall不等式，可得

即有

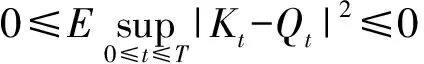
定理2若條件1)～4)成立，則數值逼近解(4)收斂于系統(1)的解析解，即滿足

4　結束語

本文討論了一種具有Markovian調制的役齡相關隨機資本系統數值解的收斂性。結果表明：在相應條件下，系統的數值逼近解(4)收斂于其解析解。

[1]MARITON M.Jump Linear Systems in Automatic Control[M].New York:Marcel Dekker，1990.

[2]YUAN C G,MAO X R.Convergence of the Euler-Maruyama method for stochastic differential equations with Markovian switching[J].Mathematics and Computers in Simulation，2004，64:223-235.

[3]WANG Z，LIU Y，YU L，et al.Exponential stability of delayed recurrent neural networks with Markovian jumping parameters[J].Physics Letters A，2006，356:346-352.

[4]戴偉星，胡適耕.帶Markov調制的隨機微分延遲方程的穩定性(英文)[J].數學研究與評論，2008，28:511-520.

[5]WANG L S，XUE H.Convergence of numerical solutions to stochastic differential delay equations with Markovian switching and Poisson jump[J].Applied Mathematics and Computation 2007，188:1161-1172.

[6]RATHINASAMY A，BALACHANDRAN K.Mean square stability of semi-implicit Euler method for linear stochastic differential equations with multiple delays and Markovian switching[J].Applied Mathematics and Computation，2008，206:968-979.

[7]RATHINASAMY A.Split-step-methods for stochastic age-dependent population equations with Markovian switching[J].Nonlinear Analysis:Real World Applications，2012，13:1334-1345.

[8]Zhou S B，Wu F K.Convergence of numerical solutions to neutral stochastic delay differential equations with Markovian switching[J].Computational and Applied Mathematics，2009，229:85-96.

[9]LI R H，HOU Y M.Convergence and stability of numerical solutions to SDDE with Markovian Switching[J].Applied Mathematics and Computation，2006，175:1080-1091.

[10]LI R H，LEUNG P K，PANG W K.Convergence of numerical solutions to stochastic age-dependent population equations with Markovian switching[J].Journal of Computational and Applied Mathematics，2009，233:1046-1055.

[11]LI R H，PANG W K，LEUNG P K.Convergence of numerical solutions to stochastic age-structured population equations with diffusions and Markovian switching[J].Applied Mathematics and Computation，2010，216:744-752.

[12]JIANG F，SHEN Y，HU J H.Stability of the split-step backward Euler scheme for stochastic delay integro-differential equations with Markovian switching[J].Communications in Nonlinear Science and Numerical Simulation，2011，16:814-821.

[13]MA W J，ZHANG Q M.，WANG Z P.Asymptotic stability of stochastic age-dependent population equations with Markovian switching[J].Applied Mathematics and Computation，2014，227:309-319.

[14]楊洪福，張啟敏.具有Markov調制的隨機年齡結構種群系統半馴服Euler法的指數穩定性[J].數學年刊A輯(中文版)，2016，37:7-88.

[15]GUO X.Information and Option Pricing[J].Quantitative Finance，2001(1):38-44.

[16]ELLIOTT R J，HINZ J.Portfolio analysis，hidden Markov models and chart analysis by PF-diagrams[J].International Journal of Theoretical and Applied Finance，2002，5:385-399.

[17]ZHANG Q M，LIU Y T，LI X N.Strong convergence of split-step backward Euler method for stochastic age-dependent capital system with Markovian switching[J].Applied Mathematics and Computation，2014，235:439-453.

[18]ZHANG Q M，LIU W A，NIE Z K.Existence，uniqueness and exponential stability for stochastic age-dependent population[J].Applied Mathematics and Computation，2004，154:183-201.

[19]ANDERSON W J.Continuous-time Markov Chains[M].Berlin:Springer，1991.

(責任編輯陳艷)

Convergence of Solution for Stochastic Capital System with Markovian Switching

ZHENG Lai-yun

(School of Mechanical Engineering, Ningxia University, Yinchuan 750021, China)

The numerical solution of a class of stochastic age-dependent capital system with Markovian switching was given according to the Euler method in time discretization. Utilizing It’s formula, Gronwall lemma and Barkholder-Davis-Gundy inequality, some criteria were obtained for the convergence of the numerical solution.

stochastic capital system; Markovian switching; It’s formula

2016-05-08

寧夏自然科學基金資助項目(NZ14048)

鄭來運(1979—),女，寧夏人，講師，主要從事運籌學與控制理論的研究，E-mail: zhenglaiyun@126.com。

format：ZHENG Lai-yun.Convergence of Solution for Stochastic Capital System with Markovian Switching[J].Journal of Chongqing University of Technology(Natural Science)，2016(10):156-162.

10.3969/j.issn.1674-8425(z).2016.10.025

O231

A

1674-8425(2016)10-0156-07

引用格式：鄭來運.具有Markovian調制的隨機資本系統數值解的收斂性[J].重慶理工大學學報(自然科學)，2016(10):156-162.