引導(dǎo)　交流　展示——基本不等式（1）的教學(xué)設(shè)計

江蘇省南通市通州區(qū)金沙中學(xué) 祝維男

引導(dǎo)交流展示——基本不等式（1）的教學(xué)設(shè)計

江蘇省南通市通州區(qū)金沙中學(xué) 祝維男

蘇霍姆林斯基指出：“在人的心靈深處，有一種根深蒂固的需要，希望自己是一個發(fā)現(xiàn)者、研究者和探索者，而在孩子的精神世界中，這種需要更強(qiáng)烈。”所以在數(shù)學(xué)課堂中我們要善于引導(dǎo)學(xué)生去合作、交流、發(fā)現(xiàn)，下面以蘇教版“基本不等式（1）”的教學(xué)設(shè)計談?wù)勎以趯嵺`中的探究摸索。

一、教學(xué)目標(biāo)

問題1：取一些數(shù)做試驗，算一算，能猜想出什么結(jié)論？

猜想結(jié)論：如果a，b是正數(shù)，那么

1.探索并了解基本不等式的證明過程。

2.體會證明不等式的基本思想方法。

3.會用基本不等式證明簡單的不等式。

二、教學(xué)重點(diǎn)、難點(diǎn)

重點(diǎn)：基本不等式的發(fā)現(xiàn)與證明并能應(yīng)用基本不等式證明簡單的不等式。

難點(diǎn)：理解基本不等式中等號成立的條件及基本不等式的幾何解釋。

三、教學(xué)方法與教學(xué)手段

采用啟發(fā)引導(dǎo)、展示交流的教學(xué)方法，以學(xué)生為課堂主體，以基本不等式為主線，從實際情景出發(fā)，放手讓學(xué)生探究思索。以flash動畫、幾何畫板、多媒體課件等作為教學(xué)輔助手段、加深學(xué)生對基本不等式的理解。

四、教學(xué)過程

1.情境引入，發(fā)現(xiàn)公式

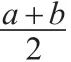
問題2：你能證明上述結(jié)論嗎？

2.代數(shù)證明，得出公式

（獨(dú)立思考—小組交流—展示成果—整理板演）

證明不等式的三種常見方法：

（1）比較法；（2）分析法；（3）綜合法。

問題：結(jié)論中的取值能推廣到一切實數(shù)嗎？

3.理解公式，加深認(rèn)識

（1）基本不等式成立的條件是什么？

（2）基本不等式中等號成立的條件是什么？

（3）基本不等式的常見變形公式。（揭示其中積與和的本質(zhì)關(guān)系）（4）幾何解釋

如圖，AB是圓O的直徑，點(diǎn)C是AB上一點(diǎn)，AC=a，BC=b。過點(diǎn)C作垂直于AB的直線交半圓于點(diǎn)D。

（利用幾何畫板，小組討論，回答下列問題）

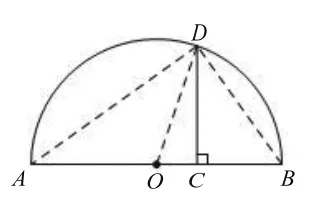
問題3：現(xiàn)在結(jié)合問題1、2能給出幾何解釋嗎？

4.應(yīng)用公式，鞏固提高

（獨(dú)立思考—展示交流—評價碰撞—整理板演）

例1 設(shè)a，b是正數(shù)，證明下列不等式成立：

問題：從上面的解題中，你學(xué)到了什么？

5.歸納小結(jié)，反思提升

問題：通過本節(jié)課的學(xué)習(xí)你能歸納出個一、二、三嗎？

（1）一個公式——基本不等式；

（2）兩個注意——注意基本不等式成立的條件，注意基本不等式中等式成立的條件；

（3）三種方法——作差法、分析法、綜合法。

6.作業(yè)布置，課后延拓

作業(yè)：課本習(xí)題3.4第2，6題。

拓展研究：1.課外查找基本不等式的其他幾何解釋，整理并交流；2.盡可能多地給出基本不等式的變形。

本節(jié)課是必修5第三章不等式的重要內(nèi)容之一，基本不等式的提出來源于實際生活，因此創(chuàng)設(shè)的問題情境應(yīng)貼近學(xué)生的生活。比較多種情境導(dǎo)入，發(fā)現(xiàn)這個“天平稱重”的導(dǎo)入既與教材一致又指向簡明、直擊主題，趣味十足。激發(fā)了學(xué)生的求知欲和探索欲。設(shè)計的遞進(jìn)問題有助于學(xué)生分析、猜想、發(fā)現(xiàn)，充分體現(xiàn)了思維的層次性。基本不等式的證明是一個重要環(huán)節(jié)，在這一過程中，引導(dǎo)學(xué)生探索用不同方法證明，總結(jié)出各種證明方法的思路和步驟，使他們能初步領(lǐng)會不等式證明的基本方法，同時培養(yǎng)他們廣泛參與和積極主動的學(xué)習(xí)品質(zhì)。基本不等式的幾何解釋是教學(xué)的難點(diǎn)，借助幾何畫板化解教學(xué)難點(diǎn)，加深學(xué)生對基本不等式的理解，進(jìn)一步領(lǐng)悟取等號的條件，體會數(shù)到形的數(shù)學(xué)思想。基本不等式的簡單應(yīng)用中，從一個問題出發(fā)，通過變題讓學(xué)生掌握應(yīng)用基本不等式證明簡單不等式的注意條件，并能經(jīng)過適當(dāng)變形引導(dǎo)學(xué)生領(lǐng)會基本不等式特征，提升解決問題能力，體會方法與策略，并為下一課時講利用基本不等式求最大（小）值做了充分的準(zhǔn)備。最后，采用數(shù)字式小結(jié)，培養(yǎng)學(xué)生對所學(xué)知識進(jìn)行概括歸納的能力，鞏固了所學(xué)知識且在作業(yè)的布置中增加了拓展研究作業(yè)，幫助學(xué)生進(jìn)一步加深了對基本不等式的認(rèn)識。