小議函數概念授課的認知思考

江蘇省南通市通州區金沙中學 錢玉飛

小議函數概念授課的認知思考

江蘇省南通市通州區金沙中學 錢玉飛

新知教學怎么演繹？傳統理念授課是否比新課程理念授課更為高效？師生教學是否真的一成不變？帶著這些疑惑，聆聽了一堂典型的傳統新知授課，與大家探討。

函數；概念；傳統；新課程；認知；思維；教學

傳統理念授課是否比新課程理念授課更為有效和高效？這是課程改革十多年圍繞教師教學的沉重話題。縱觀教學一線，在運用探究、建構，強調自主的教師眼里，新課程理念的授課正在不斷提高學生的自主學習能力，讓學生的數學學習興趣得到了提升，但是應試方面似乎有所下降；那些并未在課程改革中有所“作為”的教師，盡管在轟轟烈烈的課程改革中未曾受益，但是在以高考顯“英雄”的當下，卻仍舊是教學的主流。從主流的教學論壇，如百度貼吧等學習園地中，常常有學生如是寫道：挺喜歡數學課上的探究，通過自己研究還得到了兩平行線間的距離公式，但是一到考試總考不出！這是典型探究課堂下的學生學習感言！

我們從這些現象的背后不難產生一些思考：是不是探究式教學在今天還是難以成為教學的主流？是不是探究式教學演繹新知是低效的？對于新知授課能讓學生真正喜歡、吸收內化，教學的突破點在哪里？其實，都不是。真正的好課不在于授課教學的模式，而在于是否引發學生足夠的認知“碰撞”！我們不妨首先來看一個近期高一函數概念教學的公開課案例（教齡3年），思考為何其授課值得反思的原因：

【案例】函數概念教學片斷

師：同學們，今天我們要講的是函數概念。大家在初中已經學習過函數，老師先請一個學生回答下，你腦海中函數的概念是怎么樣的？

生1：能用這樣的形式表示的式子是函數！（草根派）

生2：好像是自變量對應一個因變量的式子叫函數。（學院派）

師：同學們有的說的很形象，有的說的有些道理。其實，函數的概念發展了上百年，到了現在才被數學家一致認可下來，我們看看是怎么定義的：對兩個非空數集A、B，集合A中的任何一個元素在集合B中有唯一的元素跟它相對應，稱這種對應關系為函數關系。其中集合A稱之為定義域，顯然函數值的集合是集合B的子集。這個問題有點像找隊友，只能一個找一個！給出問題：請判斷是否為函數：

問題1：（1）M=R，N=R+，；

（2）右邊兩幅圖；

問題2：研究下列函數定義域：

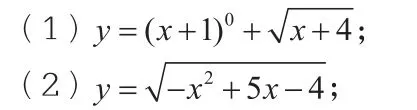
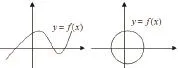
考慮到其余部分不是重點，就不一一列舉了。

【反思】

課后，教師們一起交流了這堂用傳統授課方式演繹的函數概念教學，教師首先做出了自己的設計表述：首先，考慮到開設的是一堂《必修1》1.2.1《函數的概念》的公開課。因此在備課期間，我比起關注課堂的內容更多地關注點在于如何讓學生能夠投入到課堂中來，如何讓這堂課更能夠吸引學生的興趣，故在課堂設計的時候重點放在了：

（1）函數的引入如何能夠銜接到學生已有的知識層面上；

（2）函數概念的定義解釋上如何更加趣味化；

（3）如何讓學生主動地認識到研究函數需要從其定義域、對應關系、值域出發。

在上完課之后才發現課前設計的思路在真正教學上達成的效果沒有想象中那么高并且在設計上明顯存在著欠缺。在對于數學概念教學的認識上，就以本節函數概念教學為例，缺乏一種對于整體概念和教學重難點的把握，對于教學還存在著片面性。本節課的概念教學上對法則f的理解，函數三要素的滲透不夠深刻，而這些內容的理解對之后的教學起著重要的鋪墊作用，這也是以后課堂進步的空間。再者，課堂教學的模式仍止步于解題式的教學方式，以解題的模式替代了概念教學，這樣的課堂不夠高效、活潑，對于教學活動的開展是個值得關注的問題，也是需要在之后教學中不斷提煉升華的。

課后我們一起詳細交流了一些問題，認為最值得我們教學關注的反思在于：

（1）為什么學生沒有完全掌握好這一概念？最主要的原因是教師設計的案例、問題沒有引起學生足夠的認知沖突！其實與探究式教學理念還是傳統式教學理念關系不大，關鍵是當教師把概念讀完并開始解釋概念的時候，沒有引起學生足夠的認識沖突！筆者思考：函數概念中對學生認知沖突最大的是什么？當然是對應法則f！因為只有這個抽象的表述符號才是學生最難接受函數概念的原因，這一點上探究式教學是不可能在短短四十五分鐘內做到，傳統式授課有其引導的優勢，但是引導的還是稍顯不足；

（2）教師對于學生更多的是進行引導和“再創造”，教學伊始，在課堂中教師的引導工作也有著很多學問，新教師如何規范地進行板書設計，課堂習題解答都深深地影響著學生們的學習，站上講臺后的一言一行，都是我們需要注意的。在本課問題設計中出現了一些細節問題。首先數學符號的使用不夠嚴謹，課堂上出現的一些數學符號（如R+）就在這個版本的教材中沒有涉及、對于圓的表示是不能使用符號否則易混淆函數表示，這樣的問題就暴露出課堂準備的不充足。在習題解答的環節，對于每道題目的解答上都沒有使用最好的解法，有些解法過于繁瑣，并且在書寫上沒有進行規范地安排，給學生帶來過于混亂的感覺，這些教學上的缺陷的原因則是在于教材的理解不夠清晰。

最后，筆者想說函數概念是概念教學的最核心的部分。要讓學生能夠吸收新的概念，必須要引導、設計思維的認知沖突！唯有產生與頭腦認知不匹配的沖突，才能讓學生有學習、理解的興趣。在課堂教學的設計上，教師也要站在學生的視角，更多地從學生的思維出發引發設計的“碰撞”，才能讓教學突出以生為本的原則。