一種適用于非結構網格的間斷Galerkin有限元LU-SGS隱式方法

馬明生, 龔小權, 鄧有奇, 趙 輝

1.西北工業大學 航空學院, 陜西 西安 710072 2.中國空氣動力研究與發展中心計算空氣動力研究所, 四川 綿陽 621000

?

一種適用于非結構網格的間斷Galerkin有限元LU-SGS隱式方法

馬明生1,2, 龔小權1, 鄧有奇1, 趙 輝1

1.西北工業大學 航空學院, 陜西 西安 710072 2.中國空氣動力研究與發展中心計算空氣動力研究所, 四川 綿陽 621000

具有TVD性質的顯式Runge-Kutta間斷Galerkin(RKDG)格式在CFD領域得到廣泛應用,但是顯式計算穩定性差、計算效率低。為改善時間推進效率,基于高階間斷Galerkin有限元方法,采用歐拉一階后差(BDF1),發展了一套高效的隱式LU-SGS(lower upper-symmetric Gauss-Seidel)求解方法,方法基于MPI并行實現,適合于不同計算精度。針對非線性系統左端項矩陣,對比了簡化前后LU-SGS的計算效率。建立的間斷Galerkin有限元方法基于非結構網格,采用Taylor基函數,計算精度最高達到四階精度。通過NACA0012翼型以及M6機翼算例對發展的LU-SGS方法進行了考察,與顯式算法相比,隱式格式的迭代步數和CPU時間均較大程度減小,效率能夠提高1個量級以上。最后將隱式算法用于復雜外形翼身組合體F4的流場計算,結果表明所發展的隱式方法具有較好的魯棒性,能夠用于復雜外形計算。

間斷Galerkin有限元;歐拉方程;Taylor基函數;LU-SGS;計算效率;非結構網格

隨著CFD和計算機技術的發展,CFD工作者希望得到更精細的流場結構以及更準確的氣動數據,比如阻力、力矩、熱流。精細化的網格或者高精度的計算格式是實現這些要求的途徑之一。在規則網格上進行光滑函數的數值近似,n階精度的計算格式,計算誤差與hn(h為網格尺寸)成正比。高精度格式能夠給出一些復雜流動現象的精細流場結構,相比傳統二階格式具有更高的分辨率。而非結構網格相比結構網格具有更大的靈活性,更適應復雜外形和邊界條件。因此發展適用于非結構網格的高精度格式一直是計算流體力學(CFD)研究的熱點。

間斷Galerkin有限元方法(discontinuous galerkin finite element method,DGM)是一種適合于結構網格以及非結構網格的高精度格式。它最早出現在1973年Reed和Hill[1]求解中子輸運方程問題的論文中。DGM結合了有限體積法和有限元法的優點。作為一種有限元方法,它采用有限元法中基函數思想來構造單元內的變量分布,容易實現高精度。同時它又具有有限體積法積分形式的計算形式且融入了有限體積法中數值通量、Riemann間斷、限制器等思想。DGM具有提高計算精度容易,高精度時計算模板緊致,適合非結構網格,適合處理復雜外形及復雜邊界、初值問題,并行能力強,自適應計算方便等優點。間斷Galerkin有限元方法[2]在求解守恒方程組問題中得到廣泛應用。經過Cockburn和Shu等的持續研究,一種具有TVD性質的顯式Runge-Kutta間斷Galerkin(RKDG)格式得以逐步完善。

RKDG格式單步計算時間少,內存需求量相對較小,程序容易實現,但是隨著計算精度的提高, RKDG格式對應的穩定性條件將越來越嚴格,時間推進步長受到明顯限制,計算效率低下,特別是黏性計算。一些加速技術如當地時間步長、殘值光順、多重網格等,在一定程度上加速了收斂過程。即便如此,最大的時間步長依然受到當地穩定性條件的限制。與顯式的時間格式相比,隱式方法基本不受時間推進步長的限制,因此發展高精度間斷Galerkin有限元方法的時間隱式離散方法,有著重要的工程應用價值。

目前間斷Galerkin有限元方法已有多種高效的隱式離散方法,比如帶預處理的GMRES[3]、二階的Crank-Nicholson(CN2)格式[4]、四階隱式的Runge-Kutta(IRK4)等。LU-SGS隱式方法因為其在計算效率、魯棒性及內存占用方面的優勢,在有限體積方法(FVM)中被大量采用。Yoon與Jameson在1988年[5]首先將其作為迭代方法用于方程求解,隨后Rieger和Jameson將其用于求解三維黏性流場,從此各種改進的LU-SGS隱式方法被用來求解基于結構及非結構網格的流場。詳細介紹LU-SGS在高精度間斷Galerkin有限元方法中應用的文獻較少,Haga和Wang將該方法用于基于非結構四面體網格的譜方法[6]。郝海兵、張強等在DGM四面體網格上實現了p=1階的LU-SGS迭代[7]。郭永恒在其博士論文中[8]研究了不同LU-SGS改進方法對收斂的影響。劉偉在文獻[9]中發展了基于Newton/Gauss-Seidel迭代的DGM隱式方法。

本文基于建立在非結構網格上的高精度間斷Galerkin有限元方法,發展了LU-SGS隱式計算方法,比較了不同計算精度下的收斂曲線,通過流場熵增云圖給出了不同精度下的計算結果。同時對左端項進行了簡化,給出了左端項不同簡化方法對收斂性的影響。給出了一系列二維、三維算例不同精度下的收斂曲線,比較了二階精度下有限體積和DGM下的收斂速度。

1 數值方法

1.1 控制方程

守恒形式的無黏可壓縮歐拉方程組可寫為

(1)

其中守恒變量、無黏對流通量為

(2)

ρ、u、v、w、p、E、H分別代表密度、3個方向速度、壓力、總能和總焓。

(3)

γ為比熱比。

1.2 DGM空間離散

對方程組(1)采用間斷Galerkin有限元離散。將其兩端同時乘以測試函數φi,并對整個求解域積分Ω,再采用分部積分得到如下公式

(4)

式中，?Ω為求解域Ω的邊界,n為邊界的法向量。將求解域Ω剖分為互不重疊的非結構網格單元,并對每個單元采用上面的弱形式。每個計算單元的每個守恒變量在單元內的函數分布為

(5)

uj為單元守恒變量的自由度,即為每時間步需要求解的量。N=N(p,d)由插值多項式階數p和求解的空間維數d決定。φj是階數為p的基函數。由于Taylor基函數[10]對所有單元形式都一樣且為等級基,對非結構混合網格較為合適,因此本文采用Taylor基函數。將方程(5)帶入方程(4)得

(6)

最后整個求解域方程可寫為如下形式

(7)

Res為無黏通量殘差項,由面積分和體積分構成,二者均采用高斯數值積分計算。M為全局的質量矩陣,由各單元的質量矩陣構成。無黏通量殘差項具體計算為

(8)

wv(l)、|Jl|、φil分別為體積分對應的單元高斯積分點的權系數、雅克比矩陣行列式值以及第i個基函數的梯度。ws(k)、|Jsk|、φis分別為單元面面積分對應的高斯積分點k的權系數、雅克比矩陣行列式值以及第i個基函數的值。Wak、Wbk分別對應邊界面上當前單元和相鄰單元在積分點k的變量值,Wal為當前單元體積分點l的變量值。

1.3 隱式LU-SGS方法

對方程(7)第一式采用一階歐拉后差得到

(9)

方程(9)為一大型的線性系統Ax=B,其中矩陣A為一大型稀疏塊矩陣。以三維p=3(四階精度)DGM為例,矩陣A的維數為n-cell×(5×20),n-cell為計算單元總數。如果直接存儲該矩陣并求逆,其存儲量和計算量太大,目前大多采用迭代法來求解該線性系統。

將面積分和體積分帶入左端項的Resn。

(10)

將左端項矩陣寫為

(11)

式中，D為對角塊矩陣,L為嚴格下三角矩陣,U為嚴格上三角矩陣。

為方便推導,進一步得到矩陣D、L、U,本文只寫出左端項矩陣中與當前計算單元有關的塊,將當前單元編號用a表示,相鄰單元用b表示,

對(10)式采用鏈式法則

(12)

(13)

進一步得到面積分通量對守恒變量的偏導數

(14)

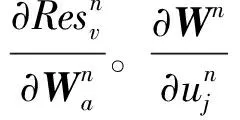
將方程(8)的第一項以及方程(14)帶入方程(12)得

(15)

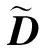
(16)

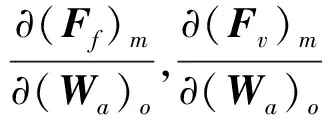
(17)

2 數值模擬結果及分析

本文首先通過等熵渦算例驗證了DGM的計算精度。為驗證本文發展的LU-SGS方法的收斂性,計算了幾類典型的測試算例。測試過程中,右端對流通量項采用Roe′s格式,并采用三階TVD-Runge-Kutta方法來對比分析。利用NACA0012翼型亞聲速算例考察了不同精度的LU-SGS收斂曲線,研究了CFL數對收斂歷程的影響,給出了左端項簡化前后的收斂曲線對比。計算了三維M6機翼亞聲速繞流,給出了不同精度的收斂曲線。最后通過F4翼身組合體給出了發展的LU-SGS隱式方法在復雜外形中的應用。在分析過程中,本文采用成熟且經過驗證的有限體積方法程序作為對比分析的參考。

2.1 等熵渦問題

等熵渦問題有精確解,用來對二維Euler問題格式的精度進行驗證,這里把問題擴展到三維問題。等熵渦問題描述的是在初始的平均流(ρ,u,v,w,p)=(1,1,1,0,1)上加入一個等熵渦,渦的大小按照(18)式給出。

(18)

式中，T=p/ρ,熵S=p/ρr,ε為渦的強度ε=5.0;計算區域取為[0,10]×[0,10]×[0,10],邊界條件按照精確解給定,時間上采用顯式三階Runge-Kutta法推進至2 s。計算采用的網格為N×N×N(N=10,20,40)六面體網格。表1給出了不同精度下的L1 Error和L2 Error,可以看到方法達到了設計的精度。

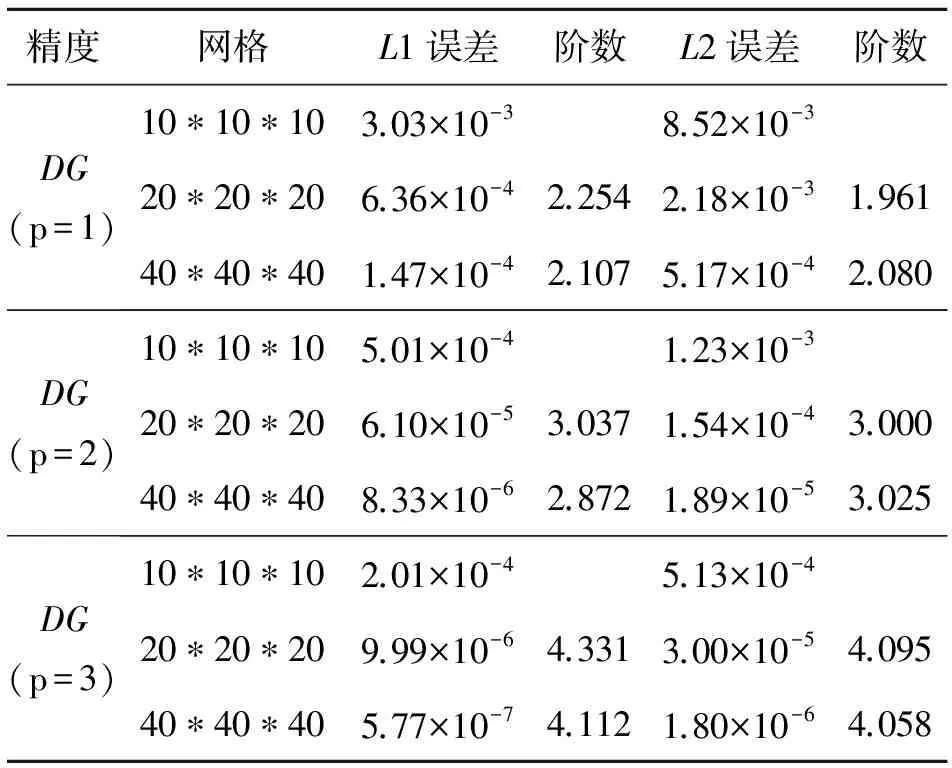
表1 等熵渦問題精度驗證(六面體網格)

2.2 NACA0012翼型亞聲速繞流

為考察DGM的精度以及發展的隱式算法的收斂性,本文計算了NACA0012翼型在來流馬赫數Ma=0.5時亞聲速繞流。計算網格如圖1所示。

圖1 NACA0012計算網格

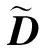
從圖3a)的曲線1和5,CFL=1,簡化左端項矩陣對收斂速度有一定影響,導致迭代步數略有增加。從圖3b)看到,對于CFL=1的情況,由于簡化左端項矩陣后,單步計算時間減小,總的收斂時間減小。由于簡化左端項矩陣后CFL數不能取大,因此未簡化左端項矩陣當CFL數取大時,其收斂速度快于簡化后的狀態。

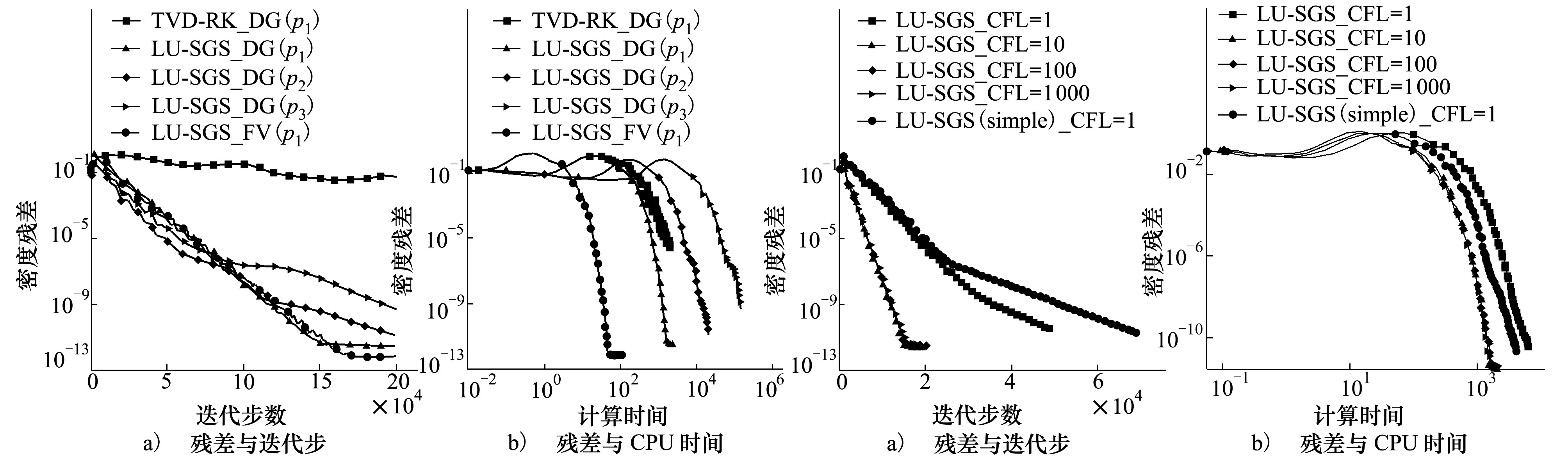
圖2 DGM不同計算精度及二階FVM收斂歷程 圖3 DGM二階精度不同CFL數收斂歷程

2.3 ONERA M6機翼亞聲速繞流

為進一步考察LU-SGS方法在三維外形計算效率,本文計算了ONERA-M6亞聲速流場,計算馬赫數Ma=0.5,迎角0°。網格如圖4所示,網格共約14萬個四面體單元,機翼前后緣及空間分別采用各向異性和各向同性四面體網格。計算采用64個CPU。

圖4 M6機翼計算網格

圖5給出了DGM不同計算精度下LU-SGS殘差收斂曲線,同時給出了FVM以及RKDG顯式結果。隱式計算的CFL=1 000,顯式計算的CFL=0.3。從殘差隨迭代步數圖看,發展的LU-SGS隱式方法收斂效率遠高于顯式方法。二階精度下,由于DGM計算的自由度為FVM的4倍且計算面通量和體積分通量時采用更多的高斯積分點,二階DGM的單步計算時間遠大于FVM。

圖5 不同計算精度DGM及二階FVM收斂曲線

2.4 DLR-F4翼身組合體亞聲速繞流

為驗證發展的隱式算法的初步工程計算能力,數值模擬了DLR-F4翼身組合體亞聲速繞流。計算網格如圖6所示。

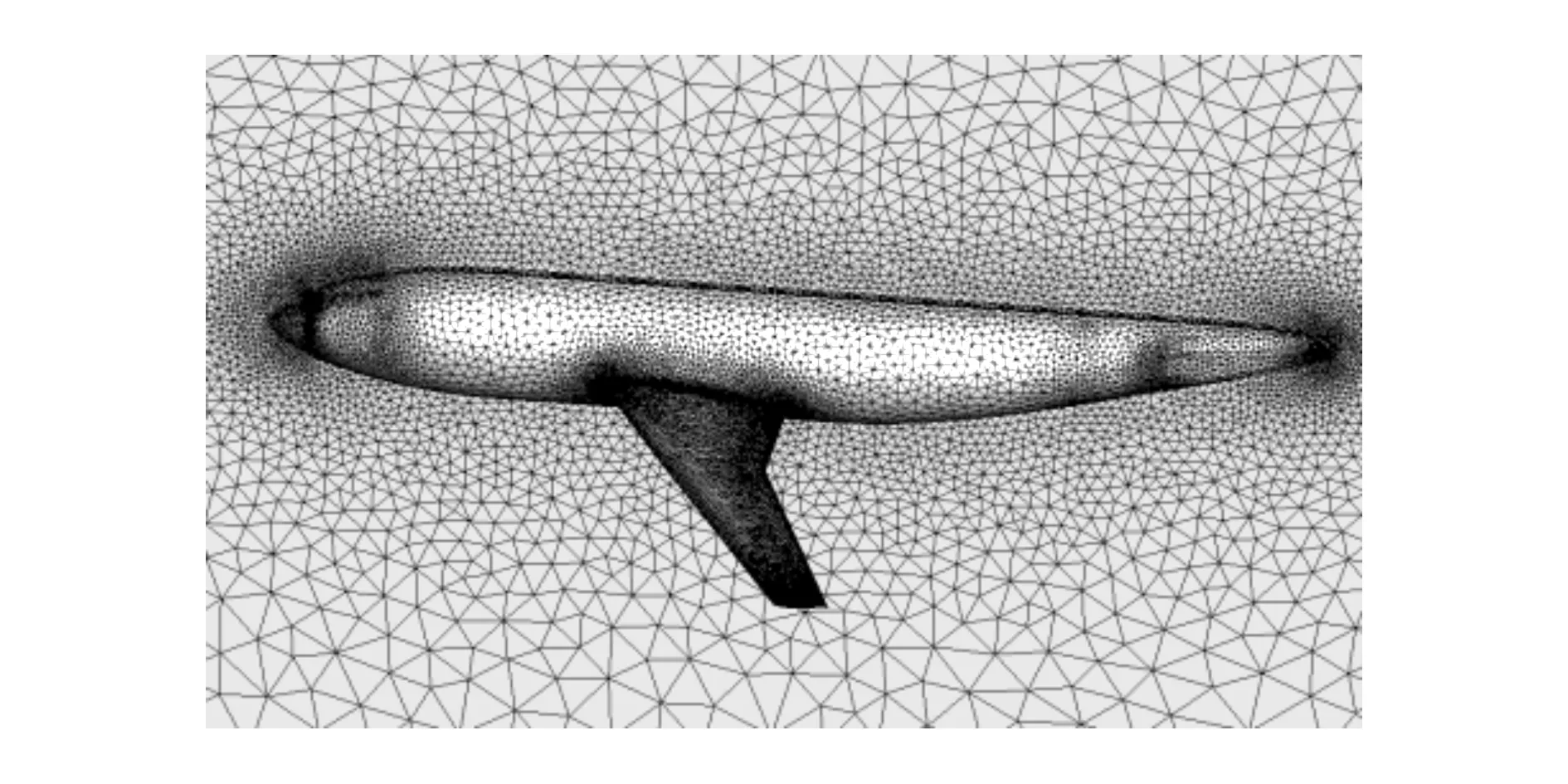
圖6 F4表面網格

四面體網格單元總數為637 126個,計算馬赫數Ma=0.5,來流迎角為0°,計算采用128個CPU,圖7給出了殘差收斂曲線,相同CFL數以及相同的dt計算方法下,相對于有線體積方法,DGM殘差收斂速度較快,但是下降量級較少。這是由于在迭代過程中DGM一直修改迭代得到的自由度,造成限制單元殘差不降,因此需要進一步研究該方法的限制器。

圖7 不同方法及精度的殘差收斂曲線

3 結 論

本文發展了一種高效的LU-SGS隱式計算方法,方法適用于不同計算精度,通過一系列的算例表明:

1) 本文發展的隱式方法CFL數能夠取很大。相比顯式RKDG,其計算效率提高了1～2個量級。

2) 發展的隱式算法對左端項殘差比較敏感,需小心簡化左端項殘差,簡化可能限制CFL數,導致整個計算時間增加,計算效率降低。

3) 隱式計算時,單元左端項矩陣包含時間項、面積分項和體積分項,單元對應的矩陣D的矩陣元素幾乎都不為零,降低了CFL數對收斂性的影響。

4) 發展的隱式方法能夠初步應用于復雜外形計算。

[1] Reed W H, Hill T R. Triangular Mesh Methods for the Neu-Tron Transport Equation[R]. Technical Report LA-UR-73-479, Los Alamos Scientific Lab, 1973

[2] Cockburn B, Shu Chiwang. TVB Runge-Kutta Local Projection Discontinuous Galerkin Finite Element Method for Conservation Laws Ⅳ: The Multidimensional Case[J]. Mathematics of Computation, 1990, 54: 545-581

[3] Persson Per-Olof, Peraire Jaime. An Efficient Low Memory Implicit DG Algorithm for Time Dependent Problems[C]∥44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2006: 9-12

[4] Wang L, Mavriplis D J. Implicit Solution of the Unsteady Euler Equation for High-Order Accurate Discontinuous Galerkin Discretizations[J]. J Comput Phys, 2007, 225:1994-2005

[5] Yoon S, Jameson A. Lower-Upper Implicit Schemes with Multiple Grids for the Euler Equatins[R]. AIAA-1986-0105

[6] Hagal Takanori, Sawada Keisuke, Wang Z J. An Implicit LU-SGS Scheme for the Spectral Volume Method on Unstructured Tetrahedral Grids[J]. Commun Comput Phys, 2009,6(5):978-996

[7] 郝海兵,張強,楊永. 基于LU-SGS迭代的DGM隱式算法研究[J]. 西北工業大學學報,2014,32(3):346-350

Hao Haibing, Zhang Qiang, Yang Yong. An Implicit Scheme of Discontinuous Galerkin Method(DGM) Based on LU-SGS Iterative Method[J]. Journal of Northwestern Polytechnical University, 2014,32(3):346-350 (in Chinese)

[8] 郭永恒. 雙曲守恒律方程組的間斷Galerkin方法研究[D]. 西安:西北工業大學,2013

Guo Yongheng. Research of Discontinuous Galerkin Method for Hyperbolic Conservation Equations[D]. Xi′an, Northwestern Polytechnical University,2013 (in Chinese)

[9] 劉偉,張來平,赫新,等. 基于Newton/Gauss-Seidel迭代的 DGM隱式方法[J]. 力學學報,2012,44(4):792-796

Liu Wei, Zhang Laiping, He Xin, et al. An Implicit Algorithm for Discontinuous Galerkin Method Based on Newton/Gauss-Seidel Iterations[J]. Acta Mechanica Sinica, 2012,44(4): 792-796 (in Chinese)

[10] Hong L, Baum J D, Lohner R. A Discountinuous Galerkin Method Based on a Taylor Basis for The Compressible Flows on Arbitrary Grids[J]. J Comput Phys, 2008, 227: 8875-8893

An Implicit LU-SGS Scheme for the Discontinuous Galerkin Method on Unstructured Grids

Ma Mingsheng1,2,Gong Xiaoquan1, Deng Youqi1, Zhao Hui1

1.School of Aeronautics, Northwestern Polytechnical University,Xi′an 710072, China 2.China Aerodynamics Research and Development Center,Mianyang 621000, China

The TVD explicit Runge-Kutta discontinuous Galerkin(TVD-RKDG) are widely used in CFD, but it has poor stability property and low computational efficiency. To improve the time advancing efficiency, an efficient implicit lower-upper symmetric Gauss-Seidel (LU-SGS) scheme based on backwards differencing methods (BDF1) has been applied to the high-order discontinuous Galerkin method. The method is implemented parallelly through MPI library and is suit for different computational orders. The left matrix of nonlinear system is simplified and computational efficiency is compared. The DGM is based on the Taylor basis functions on unstructured grid and the accuracy is up to forth order. The developed LU-SGS scheme is verified through NACA0012 airfoil and ONERA M6 wing. Compared to the traditional explicit Runge-Kutta scheme, the implicit scheme can greatly reduce the iteration number and CPU time. The computational efficiency can be accelerated evidently with more than one order of magnitude speed. At last the flow field of DLR-F4 is simulated to verify the robustness of the developed implicit scheme. The result proves that the developed LU-SGS scheme can be applied to complex configuration simulation.

discontinuous Galerkin method; Euler equations; Taylor basis; LU-SGS; computational efficiency; unstructured grid

2016-03-20

馬明生(1962—)，西北工業大學兼職教授，主要從事飛行器設計與計算流體力學研究。

V211.3

A

1000-2758(2016)05-0754-07