基于微分對策的水下主動防御攔截導引方法

程瑞鋒, 劉衛東,2, 高立娥,2, 張建軍

(1.西北工業大學 航海學院, 陜西 西安 710072; 2.西北工業大學 水下信息與控制重點實驗室, 陜西 西安 710072)

?

基于微分對策的水下主動防御攔截導引方法

程瑞鋒1, 劉衛東1,2, 高立娥1,2, 張建軍1

(1.西北工業大學 航海學院, 陜西 西安 710072; 2.西北工業大學 水下信息與控制重點實驗室, 陜西 西安 710072)

針對來襲水下目標機動方式的無法預知的問題,為實現精確攔截,以目標捕獲條件為約束,設計了一種用于水下機動目標攔截的微分對策導引律。以微分博弈理論為基礎,構造用于雙邊最優控制的二次型性能指標,利用伴隨原理求解終端問題的方法導出具有狀態反饋形式“零效脫靶量”,并以其為性能指標設計用于航向角控制的微分對策制導律。通過對機動目標的跟蹤攔截表明:該制導律對目標機動方式具有較強的魯棒性,與最優導引相比,對機動目標的攔截精度高,可滿足水下攔截作戰技術需求。

微分對策;制導律;攔截;脫靶量

隨著水下智能武器系統識別和跟蹤能力的增強,實施以“硬殺傷”為主的水下主動防御攔截成為當前海戰防御的研究熱點。由于水下攔截器與來襲目標均屬水下兵器,基于現有水下兵器結構的制約,水下攔截器與來襲目標相比,在航速和機動性方面并不占優勢,但所攔截的目標卻具有速度快、尺寸小及機動性強的特點[1]。同時,在攔截對抗過程中,雙方都屬于獨立控制,且目標機動策略一般無法預測,在未知目標機動信息情況下實施對來襲目標的最優攔截非常困難。

微分對策控制是最優控制與對策論的有效融合[2],在處理對抗問題上具有明顯優勢。目前,微分對策已廣泛應用到導彈攔截決策方面,文獻[3]研究了彈目對抗的線性二次微分對策導引律;文獻[4]應用研究了臨近空間導彈攔截大機動目標的微分對策攔截制導律;文獻[5]研究了目標機動信息時延可知情形的導彈攔截微分對策制導律。上述研究結合微分對策理論,提出了雙方動態控制的微分對策制導律,通過有效控制使視線角速度趨于零,達到了優化攔截控制系統性能的目的。然而,由于水下攔截器的自導裝置與殼體固連,且受水聲物理場的制約,其探測范圍和精度受到一定限制,同時由于聲自導的波束較寬,往往在10°左右,加上水聲傳播信息量少,對目標的測量僅有距離或方位,難以利用目標所在波束的變化及攔截器航向角來推算視線轉動速率[6],所以在水下防御攔截中直接應用現有的攔截微分對策制導律應用受到很大限制。本文充分考慮復雜水文條件對水下攔截器自導系統的影響,在已知來襲目標方位和距離或僅知目標方位信息實施的有利提前角角發射基礎上,以攔截器捕獲來襲目標條件為約束條件,提出了一種基于微分對策的主動防御攔截導引方法,使水下攔截器通過實時“零效”跟蹤,實現對來襲目標的有效攔截。

1 問題描述

在海戰中,我方艦潛接到來襲報警時,一般只能探測來襲目標所在方位和大致距離,為爭取時間,盡快發射攔截器進行反擊,在未知來襲目標航行方向和航速以及準確距離條件下,根據圖1所示的攔截器對抗來襲目標陣位關系確定攔截器的發射角范圍。

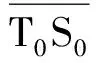
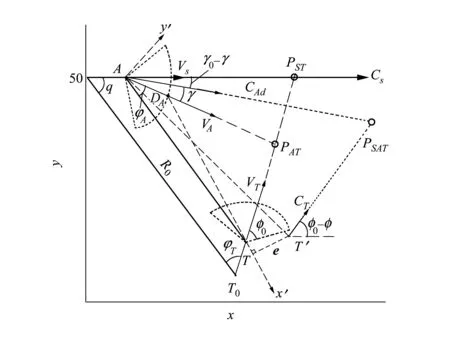
圖1 攔截器對抗來襲目標陣位關系

(1)

由于多波束自導裝置在水中兵器上的應用及自導作用距離的存在,當我方按正常提前角向相遇點AT發射攔截器時,只有當攔截器的自導扇面的前端中點DA與來襲目標構成相遇三角形TDAPA時,捕獲概率方為最高[7]。為實現快速精確導引,須將攔截器與來襲目標的“瞬時相遇點”始終捕獲在自導裝置中間波瓣內。假定自導攔截時,攔截器的側滑角很小,即可將攔截器的縱軸近似為攔截器的速度矢量方向。在攔截導引末段,由于觀測誤差和目標機動的存在,來襲目標往往偏離所在自導捕獲波瓣,此時,攔截器須通過實時調整航向角變化γ來獲得對目標的最高捕獲概率,從而確保攔截器的精確導引和有效攔截。

2 微分對策制導律的設計

在末制導導引攔截中,攔截器同樣進入了來襲目標的可探測區域,此時來襲目標能夠感知攔截意圖,從而進行機動規避。由于雙方均屬于獨立控制,為使攔截器實施對來襲目標的最佳捕獲和有效攔截,根據圖2制導原理圖,結合微分博弈對策理論對上述攔截問題進行數學建模。

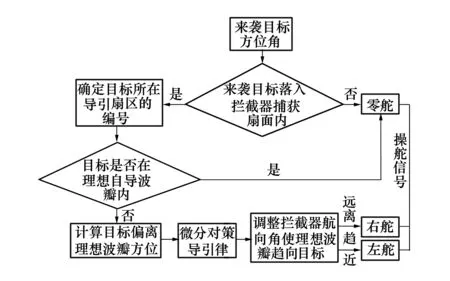
圖2 基于微分對策制導攔截導引原理圖

由圖2可知,實施有效微分對策導引的首要條件是捕獲目標。根據圖1,當來襲目標機動到T′,航向角變化為φ時,在坐標系Ax′y′中,目標的實際瞄準與期望瞄準之間產生一定的偏差,有

yT-yA=e

(2)

式中，vR是Sx′方向的相對接近速度。攔截結束時間可由tf=R0/vR近似求得。此時,任一導引時間內來襲目標方位表示為

xTi=xT(i-1)+VTΔtcosφ0+esinq+vRΔtcosq

(3)

攔截器的瞬時方位為

(4)

攔截器捕獲目標的條件表示為

(5)

式中，λ為攔截器自導扇面半角,r為攔截器的自導作用距離,γ0為攔截器初始航向角,γ為航向角變化量。以攔截器捕獲目標為約束條件,取偏差e為變量x1,則有

(6)

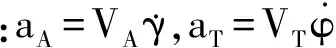
(7)

考慮工程應用性,假定攔截器具有延時時間常數為τA的一階動態特性,來襲目標發現攔截后,實施固有頻率為w的蛇形機動規避, 則有

(8)

(9)

式中

實際對抗中,作為主控方的水下攔截器所需的自身運動信息可通過自身傳感器來獲取,具有完全狀態信息,而作為攔截方的來襲目標則具有被噪聲干擾的觀測信息。因此可利用攔截器的信息優勢,通過利用對來襲目標的估計誤差來改善自己的控制策略。

根據微分對策原理,攔截器與來襲目標均尋求相應性能指標的最大化或最小化,且最終對抗目標時尋求偏差e的各分量在任何時刻都為零。則二次型性能指標為

(10)

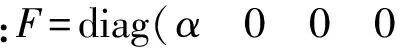
(11)

構造哈密頓-雅克比方程利用伴隨原理求解終端狀態的方法,根據性能約束(10)式對(9)式進行求解可得

(12)

式中，tgo為待航時間。當目標不機動時,tgo=tf-t,而tf可以有制導初始時刻的相對距離除以相對速度獲得。但當目標機動時,所需終止時間會產生較大的計算誤差,從而導致待航時間的估計誤差。考慮到機動過程中相對距離隨時間不斷變化,采用滾動時域法,將待航時間用tgo=RAT(t)/vR進行滾動預測,有效避免了待航時間的估計誤差。令x=tgo/τA,Z為零效脫靶量,其物理意義為攔截器從當前時刻到制導終止不再輸出控制指令,而來襲目標任然按以前的機動方式運動,到制導結束時最終獲得的兩者之間的最小距離[9]。由龐特里亞金極值原理可得攔截器的微分對策制導最優控制策略為

(13)

為了削弱線性開關函數sgn帶來的抖動,用連續函數x/(|x|+δ)來代替符號函數sgn,則攔截器制導律表示為

(14)

轉化為攔截器的角速度控制為

(15)

將(12)式代入(14)式并將系數簡化,表示為

w*=C1x1+C2x2-C3x3+C4x4+C5x5

(16)

則對應當前時刻的航向角為

(17)

由(16)式可推出具有捕獲約束的攔截器的微分對策制導反饋控制原理見圖3。

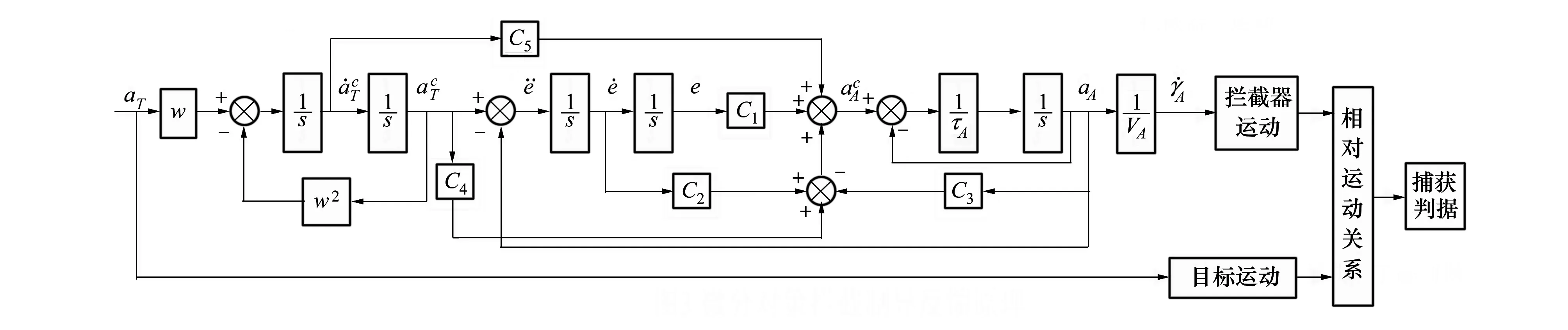
圖3 微分對策攔截制導反饋原理

3 仿真分析

假設我方艦艇在初始方位為(0,800)時,發射航速為20kn的攔截器對初始方位為(600,0)航速為20kn的來襲目標進行攔截。考慮到水下探測的難度和目標的機動,選取攔截器的自導扇面半角為60°,當相對距離小于500m時,目標實施蛇形機動規避。假定攔截器有效攔截毀傷半徑為10m,為保證來襲目標始終在攔截器的捕獲范圍內,以有效捕獲目標為約束前提進行導引律的設計,對攔截器進行最優導引(OG)和微分對策制導(DG)到導引性能進行仿真比較。

由4圖攔截蛇形機動目標運動軌跡可知,來襲目標在航行初始段不機動時,攔截器采用微分對策導引和最優導引的航跡幾乎重合。當目標發現攔截器并實施蛇形機動規避時,采用微分對策制導導引可以很好的完成攔截,且末端攔截彈道平直,而采用最優導引時使攔截軌跡發生彎曲而脫靶。

由圖5可知,在導引段采用兩種制導的跟蹤角變化率為0,即在此階段能操縱攔截器改變速度矢量并力圖使其指向瞬時遭遇點。在失穩段,結合圖6變化趨勢可知,當相對距離趨向毀傷半徑時,采用微分對策制導的法向過載趨向0,使攔截器在進入導引頭盲距(死區)前使控制面處于中立位置。而最優導引則在相對距離較大時發生脫靶。

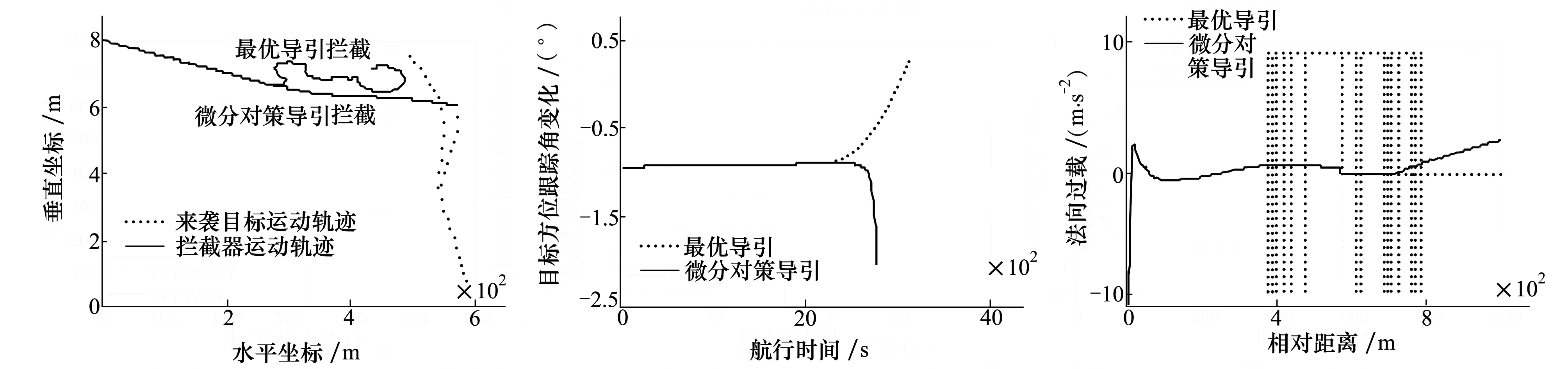
圖4 攔截蛇形機動目標運動軌跡 圖5 目標方位角跟蹤變化趨勢 圖6 法向過載隨相對距離的變化趨勢

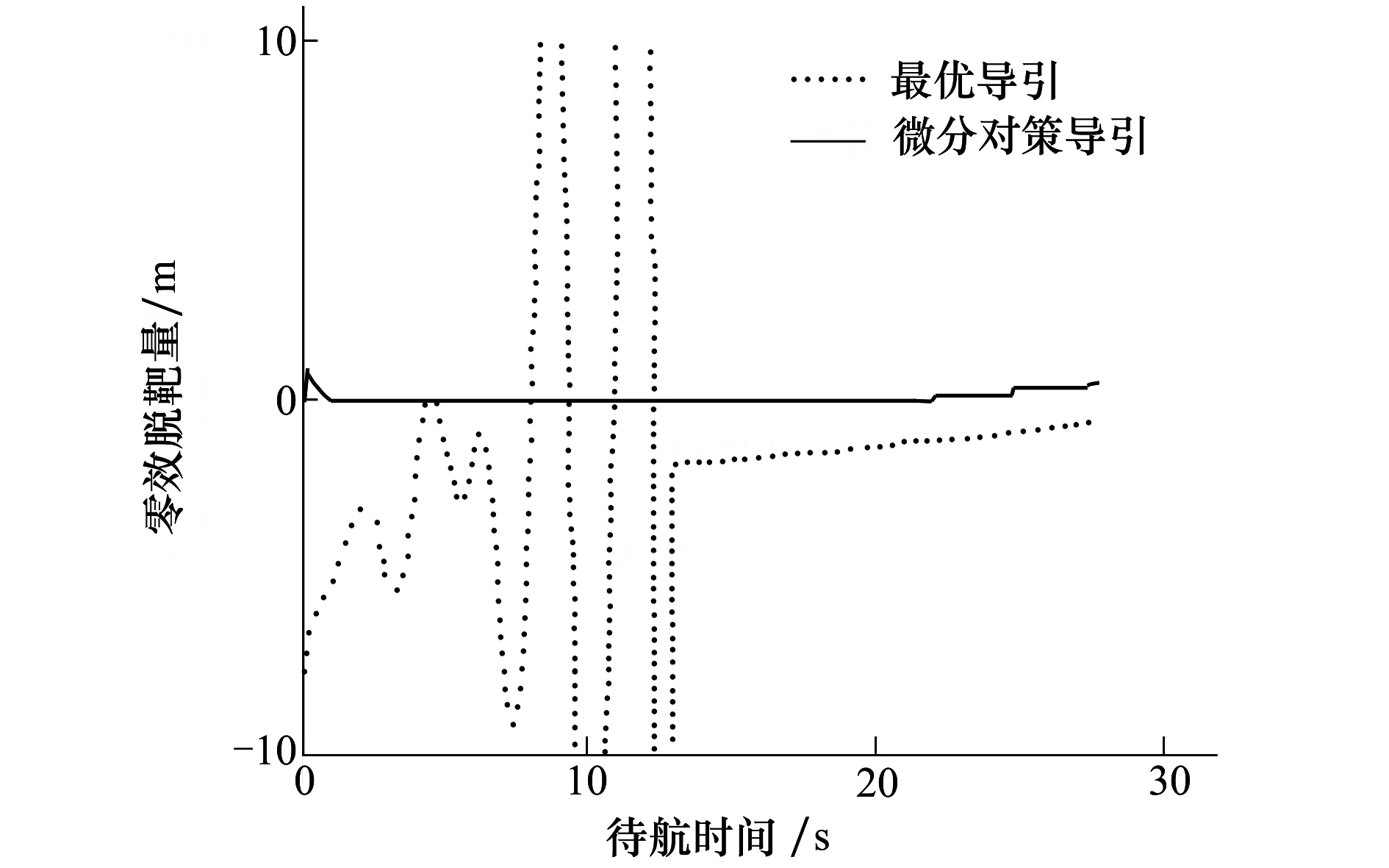
圖7 零效脫靶量變化趨勢

由圖7所示的零效脫靶量變化趨勢可以看出,當目標機動時,采用微分對策導引的“零效脫靶量”在初始段進行調整后,保持在零位附近小幅波動,而采用最優導引的零效脫靶量波動劇烈。

當來襲目標分別采用非機動、單純加速機動和隨機蛇形機動方式進行規避時,攔截器采用最優導引與微分對策導引的攔截結果見表1。

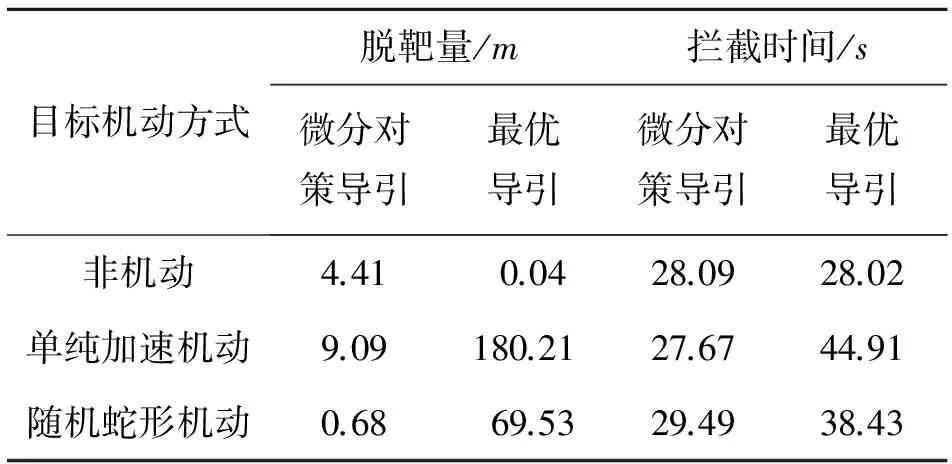
表1 不同機動方式目標的微分對策攔截結果

由表1可知,對于非機動目標,攔截器采用最優導引的攔截效果優于采用微分對策導引所獲得的攔截效果,但當目標機動時,最優導引制導效果明顯下降。當目標機動單一時,采用微分對策制導可以有效完成攔截任務,相比最優導引具有一定的優勢。當目標機動性增強時,采用微分對策進行導引攔截可以在較短的時間實現對機動目標的成功攔截,優勢明顯。

4 結 論

基于水下目標捕獲條件,提出了一種用于水下攔截器迎面攔截的微分對策制導律。

1) 該制導的設計充分考慮水下武器捕獲目標的限制,以目標捕獲約束模型作為微分對策制導的控制量的飽和約束條件,有效保證了攔截效果;

2) 該制導律的設計以“博弈”對抗理論為基礎,以時間和能量消耗為性能指標,利用伴隨原理求解終端問題的方法導出作為反饋控制的“零效脫靶量”,并通過滾動時域法對待航時間進行估計,保證了攔截的穩定性和終端命中精度。

3) 仿真結果表明,相對于最優導引攔截,該制導律能實施對來襲機動目標的有效攔截,且目標機動性越強,優勢越明顯,對工程應用具有一定的參考價值。

[1] 陳春玉. 反魚雷技術[M]. 北京: 國防工業出版,2006

ChenChunyu.Anti-TorpedoTechnology[M].Beijing,NationalDefenseIndustryPress, 2006 (inChinese)

[2] 方洋旺,伍友利,王洪強,等. 導彈先進制導與控制理論[M]. 北京:國防工業出版社,2015

FangYangwang,WuYouli,WangHongqiang,etal.MissileAdvancedGuidanceandControlTheory[M].Beijing,NationalDefenseIndustryPress, 2015 (inChinese)

[3] 花文華,陳興林. 高階控制導彈線性二次型微分對策制導律[J]. 固體火箭技術,2011,34(4):403-407

HuaWenhua,ChenXinglin.LQGDifferentialGameGuidanceLawforHigh-OrderControlledMissiles[J].JournalofSolidRocketTechnology, 2011,34(4): 403-407 (inChinese)

[4] 田進,李言俊. 臨近空間防空導彈制導律[J].火力與指揮控制, 2012,37(3): 87-89

TianJin,LiYanjun.ResearchonGuidanceLowforNearSpaceAirDefenceMissil[J].Firecontrol&CommandControl, 2012,37(3): 87-89 (inChinese)

[5]SimoneBattistini,TalShima.DifferentialGameMissileGuidancewithBearing-OnlyMeasurements[C]∥52ndIEEEConferenceonDecisionandControl, 2013: 4218-4223

[6] 石秀華,王曉娟. 水中兵器概論(魚雷分冊)[M]. 西安:西北工業大學出版社,2005

ShiXiuhua,WangXiaojuan.IntroductiontoUnderwaterWeapons(TorpedoBooklet)[M].Xi′an,NorthwesternPolytechnicalUniversityPress, 2005 (inChinese)

[7] 陳顏輝,黃文斌,孫振新. 最優規避魚雷策略與最小可規避預警距離[J]. 海軍工程大學學報,2014,2(26):76-81

ChenYanhui,HuangWenbin,SunZhenxin.OptimalEludingStrategyandMinimalAvoidableAlarmDistanceagainstTorpedo[J].JournalofNavalUniversityofEngineering, 2014,2(26): 76-81 (inChinese)

[8] 李登峰. 微分對策及其應用[M]. 北京:國防工業出版社,2000

LiDengfeng.DifferentialGamesandApplication[M].Beijing,NationalDefenseIndustryPress, 2000 (inChinese)

[9] 雷虎民,張旭,董飛垚,等. 零控脫靶量有限時間收斂制導律[J]. 國防科技大學學報, 2015,3(37):136-142

LeiHumin,ZhangXu,DongFeiyao,etal.FiniteTimeConvergentZero-EffortMissGuidanceLaw[J].JournalofNationalUniversityofDefenseTechnology, 2015,3(37): 136-142 (inChinese)

[10] 孫勝,張華明,周荻. 考慮自動駕駛儀動特性的終端角度約束滑模導引律[J]. 宇航學報,2013,34(1):69-78

SunSheng,ZhangHuaming,ZhouDi.SlidingModeGuidanceLawwithAutopilotLagforTerminalAngleConstrainedTrajectories[J].JournalofAstronautics, 2013,3(37): 69-78 (inChinese)

[11] 陳峰,肖業倫,陳萬春. 基于零控脫靶量的大氣層外超遠程攔截制導[J]. 航空學報,2009,30(9):83-59

ChenFeng,XiaoYelun,ChenWanchun.GuidanceBasedonZeroEffortMissforSuper-RangeExoatmosphericIntercept[J].ActaAeronauticaetAstronauticaSinica, 2009, 30(9): 83-59 (inChinese)

[12] 李運遷. 大氣層內攔截彈制導控制及一體化研究[D]. 哈爾濱:哈爾濱工業大學,2011

LiYunqian.IntegratedGuidanceandControlforEndo-AtmosphericInterceptors[D].Harbin,HarbinInstituteofTechnology, 2011 (inChinese)

[13] 鄭立偉,荊武興,谷立祥. 一種適用于大氣層外動能攔截器的末制導律[J]. 航空學報,2007,28(4):953-958

ZhengLiwei,JingWuxing,GuLixiang.ATerminalGuidanceLawforExoatmosphericKillVehicle[J].ActaAeronauticaetAstronauticaSinica, 2007,28(4): 953-958 (inChinese)

[14]ShimaT.OptimalCooperativePursuitandEvasionStrategiesagainstaHomingMissile[J].JournalofGuidance,Control,andDymamics, 2011,34(2): 14-25

[15] 張士熊,劉新學,李斌,等. 基于微分對策的攔截末段突防導彈機動突防制導律研究[J]. 導彈與航天運載技術, 2015(2): 81-86

ZhangShixiong,LiuXinxue,LiBin,etal.StudyonManeuverPenetrationGuidanceLawofBallisticBasedonDifferentialGamesinTheTerminalofInterception[J].MissilesandSpaceVehicles, 2015(2): 81-86 (InChinese)

Underwater Active Defense Intercept Guidance Method Based on Differential Game

Cheng Ruifeng1, Liu Weidong1,2, Gao Li′e1,2, Zhang Jianjun1

1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China;2.Science and Technology on Underwater Information and Control Laboratory,Northwestern Polytechnical University, Xi′an 710072, China

The differential game guidance law is designed for intercepting the underwater maneuvering target precisely with the constraint conditions that the interceptor must capture the targets in considering of the unpredictability of the actual target maneuver. Based on the differential game theory, the bilateral optimal control quadratic performance index is combined, and the zero miss-distance with the state-feedback is derived by adopting the method of adjoint principle to solve the terminal problem, which can is used as the index of the differential guidance law to control the head angle of the interceptor. The results show that the presented guidance law guarantees perfect intercept for intercept for maneuvering target and has good robustness to target maneuver. Compared with optimal guidance, the different maneuvering target can be intercepted more effectively, which can meet the demand of underwater interception war techniques.

the differential game; guidance law; interception; miss distance

2016-04-06

水下信息與控制重點實驗室基金(9140C230202150C23001)與國家自然科學基金(61473224)資助

程瑞鋒(1980—)，西北工業大學博士研究生，主要從事水下航行器控制與仿真研究。

TJ63

A

1000-2758(2016)05-0851-06