基于擴張干擾觀測器的再入飛行器終端滑模控制

周軍, 趙金龍

(西北工業大學 精確制導與控制研究所, 陜西 西安 710072)

?

基于擴張干擾觀測器的再入飛行器終端滑模控制

周軍, 趙金龍

(西北工業大學 精確制導與控制研究所, 陜西 西安 710072)

針對再入滑翔飛行器存在時變非匹配不確定干擾的問題,設計了一種非線性擴張干擾觀測器和新型雙回路非奇異終端滑模控制律。首先將觀測器狀態變量擴張為干擾及其變化速率的估計值,再基于Lyapunov穩定性定理設計新型非線性干擾觀測器;將再入飛行器系統方程分為姿態角外回路和姿態角速率內回路,分別設計具有干擾補償作用的新型滑模面,以及能夠有限時間收斂的非奇異終端滑模控制律。仿真結果表明,該方法可將傳統非線性干擾觀測器的估計精度提高約4%,控制系統跟蹤誤差得到明顯降低,具有良好的動態特性。

非線性干擾觀測器;再入飛行器;非奇異;終端滑模控制

再入滑翔飛行器具有飛行速度高、機動能力強等諸多優點,是突破敵方反導防御系統的利器。但其由于飛行時間長,飛行環境復雜多變,系統動力學特性呈現出強非線性、強耦合、快時變的特點,而時變的外部不確定性干擾,進一步增加了控制系統設計的難度[1-3]。

針對不確定非線性系統的控制問題,傳統的魯棒控制律過于保守,而滑模控制律則僅對系統匹配不確定干擾具有魯棒性：通過干擾觀測器技術對外部擾動進行前饋補償，有利于降低控制系統增益，獲得更好的快速性和跟蹤性能，控制指令也更為平滑，因此,基于干擾觀測器的控制系統設計成為主要方法,如滑模干擾觀測器等[4-6],但非匹配不確定系統的控制一直是設計難點。文獻[7]則首次針對非匹配不確定項設計了一種有效的非線性干擾觀測器(nonlinear disturbance observer,NDO)及相應滑模控制方法。該方法一經提出便引起了學者們的廣泛關注,并與多種非線性控制方法相結合,如自適應反演控制、動態逆控制、自適應滑模控制等[8-10]。傳統的非線性干擾觀測器均假設干擾變化緩慢,或干擾變化速率近似為零,但對于再入滑翔飛行器而言,外部干擾通常為快時變的,因此,NDO方法的應用具有極大的限制。文獻[11]則在傳統NDO的基礎上,設計了一種能夠同時觀測外部干擾及其變化速率的線性干擾觀測器,并對文獻[7]中的滑模面進行了改進，但并不適用于非線性系統。

本文即在文獻[11]的基礎上,首先基于Lyapunov穩定性定理重新設計了一種擴張狀態的非線性干擾觀測器,能夠同時觀測干擾大小及其變化速率。以具有二階不確定性干擾的再入滑翔飛行器為研究對象，根據奇異攝動理論，將系統運動方程分為姿態角外回路和姿態角速率內回路,設計了新型滑模面及雙回路非奇異終端滑模控制律,能夠基于干擾觀測數據對外部擾動進行補償，并保證控制系統跟蹤誤差在有限時間內收斂至零。最后，通過仿真對比驗證了該方法的有效性。

1 問題描述

以面對稱的再入滑翔飛行器為研究對象,忽略地球自轉的影響,系統姿態運動學和動力學方程可表示為

(1)

式中,α、β和γv分別為飛行器攻角、側滑角和傾側角;ωx、ωy和ωz為滾轉、偏航和俯仰角速率;θ為彈道傾角;m和V分別為飛行器質量和飛行速度; Jx、Jy、Jz和Jxy為飛行器慣性積;Y和Z分別為飛行器升力和側向力;Mx、My和Mz為飛行器滾轉、偏航和俯仰力矩,可表示為

(2)

式中,q為動壓,S和L分別為參考長度和參考面積;δx、δy和δz為飛行器三通道等效舵偏。

根據奇異攝動理論,飛行器六自由度運動模型(1)可描述為快回路和慢回路

(3)

式中,x1=[α β γv]T為慢回路狀態向量,x2c為慢回路虛擬控制向量,并作為快回路狀態跟蹤指令向量;x2=[ωxωyωz]T為快回路狀態向量;u=[δxδyδz]T為快回路控制向量;d1和d2為外部不確定干擾向量。

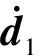
本文即針對上述含有時變不確定干擾的非線性系統,設計一種新型擴張干擾觀測器同時觀測干擾大小和變化速率,并基于此進行有限時間收斂的非奇異終端滑模控制系統設計,以提高系統抗擾動能力。

2 非線性擴張干擾觀測器設計

系統(3)中的雙回路子系統可統一表示成含有時變不確定性的多輸入多輸出系統

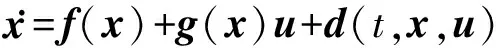
(4)

針對上述系統的控制方法通常包括2種:①基于不確定性上下界的魯棒控制律,但參數過于保守,且動態特性難以保證;②基于干擾觀測器的控制方法。傳統的非線性干擾觀測器結構簡單,運算量小,但均假設干擾變化速率近似為零,因此,對于快時變不確定性的估計精度有限[6]。

文獻[12]對傳統非線性干擾觀測器進行了改進,放寬了對干擾變化速率的限值,在干擾變化速率存在未知上界的條件下能夠保證觀測誤差有界收斂,但無法精確估計干擾變化速率,且保守性較強。本文在此基礎上,結合文獻[11]中的線性擴張干擾觀測器,進一步設計了一種非線性的擴張干擾觀測器

(5)

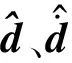
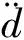
證明 首先定義觀測誤差向量如下

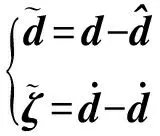
(6)

(7)

(8)

(9)

式中

(10)

對于任意給定的對稱正定矩陣Q,總能找到一個對稱正定矩陣P,使得

DTP+PD=-Q

(11)

取Lyapunov函數V=eTPe,對其求導可得

≤2‖e‖‖PH‖μ-eTQe

(12)

式中,λm為矩陣Q的最小特征值。

因此,由λm‖e‖-2‖PH‖μ=0可知,觀測誤差向量e的范數將漸進收斂于

(13)

3 雙回路非奇異終端滑模控制律設計

將再入滑翔飛行器六自由度模型分為姿態角外回路和姿態角速率內回路,分別設計基于本文干擾觀測器的非奇異終端滑模控制律,首先給出如下引理[13]:

引理1 如果存在一個連續的正定函數V(t)滿足如下不等式

(14)

則V(t)將在有限時間內收斂至系統平衡點,且收斂時間ts滿足

(15)

式中:α>0,λ>0,0<γ<1。

3.1 慢回路非奇異終端滑模控制律設計

針對再入飛行器運動模型(3)中的姿態角慢回路,首先在文獻[7]的基礎上,設計一種新型滑模面如下

(16)

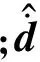
對(16)式取微分可得

(17)

定理2 對于含有時變不確定向量的慢回路系統方程(3),如果采用如下所示虛擬控制量

(18)

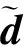
證明:設計Lyapunov函數如下

(19)

對V1取微分可得

(20)

由(20)式和引理1可知,慢回路系統狀態指令跟蹤誤差將在有限時間內到達滑模面,并漸進趨于零。

慢回路虛擬控制量x2c經過濾波環節后,作為姿態角速率快回路的狀態跟蹤指令向量。

3.2 快回路非奇異終端滑模控制律設計

針對再入飛行器運動模型(3)中的快回路方程,與(16)式類似,滑模面可設計為

(21)

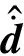
對(21)式取微分可得

(22)

定理3 對于含有時變不確定向量的快回路系統方程(3),如果采用如下所示控制律

(23)

證明:設計Lyapunov函數如下

(24)

對V2取微分可得

(25)

由(25)式和引理1可知,快回路系統狀態指令跟蹤誤差同樣將在有限時間內到達滑模面,并漸進收斂至零。

4 仿真分析

以某型再入滑翔飛行器為算例,對本文提出的非線性擴張干擾觀測器及雙回路非奇異終端滑模控制方法進行仿真分析。飛行器高度為60km,飛行馬赫數20,系統狀態初值設為

外回路中,攻角、側滑角、傾側角通道的非匹配不確定干擾分別設置為

擴張的非線性干擾觀測器函數向量取為

對應的觀測器增益矩陣為

此外,將滑模控制律中的符號函數sign(σ)替換為sigmoid函數,以降低系統抖振[14]

(26)

式中,本文取τ=50。

在Matlab/Simulink仿真環境下,對基于傳統非線性干擾觀測器的滑模控制方法(NDO-SMC)和本文基于擴張非線性干擾觀測器的雙回路非奇異終端滑模控制方法(ENDO-SMC)進行對比,結果如圖1～圖7所示。

圖1所示為俯仰、偏航、以及滾轉通道中干擾觀測結果對比,分析可知,2種非線性干擾觀測器均能夠較為準確的觀測未知擾動,但本文的ENDO方法能夠將傳統NDO的觀測精度提高約4%,有利于改善控制系統效果。

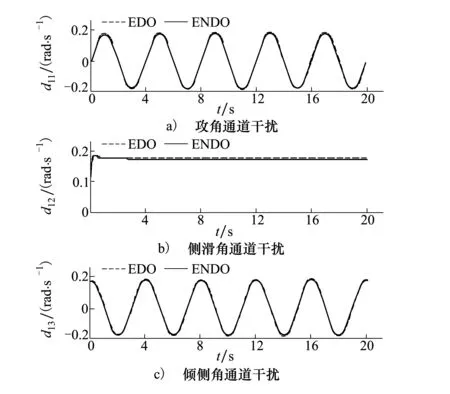
圖1 三通道干擾觀測曲線

圖2至圖7所示為攻角、側滑角、傾側角指令跟蹤曲線,以及三通道等效舵偏仿真結果對比,可見,本文的ENDO-SMC方法能夠有效提高系統控制精度,其中攻角跟蹤誤差最大降低50%,側滑角跟蹤誤差最大降低80%,等效舵偏角指令也較傳統NDO-SMC方法更為平滑,高頻抖振明顯減弱。

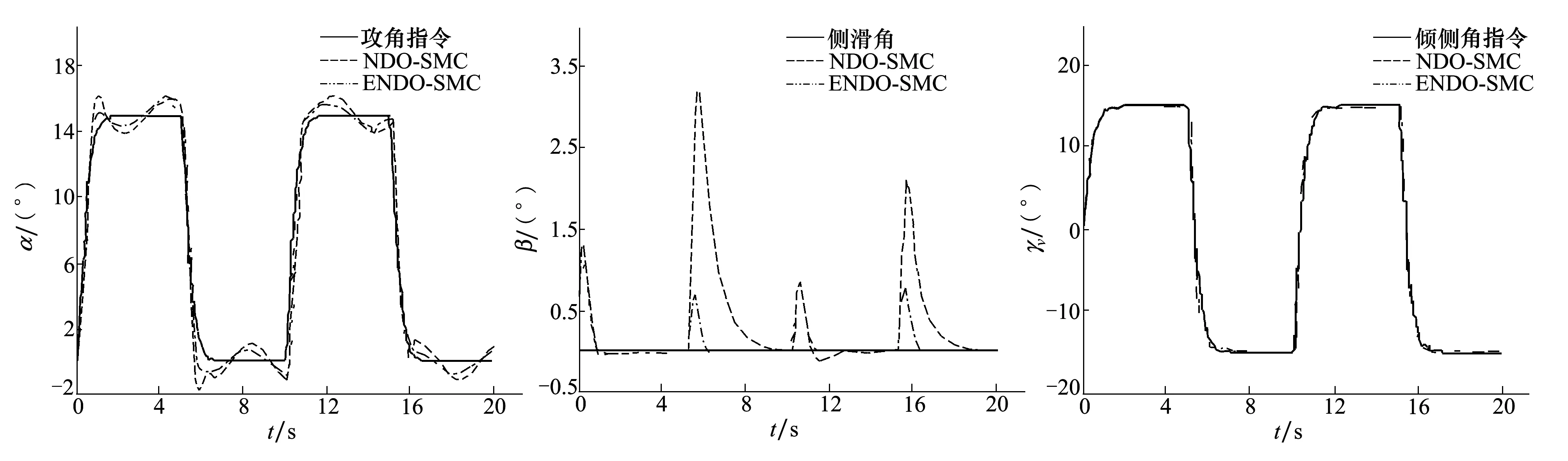
圖2 攻角指令跟蹤曲線 圖3 側滑角指令跟蹤曲線圖4 傾側角指令跟蹤曲線

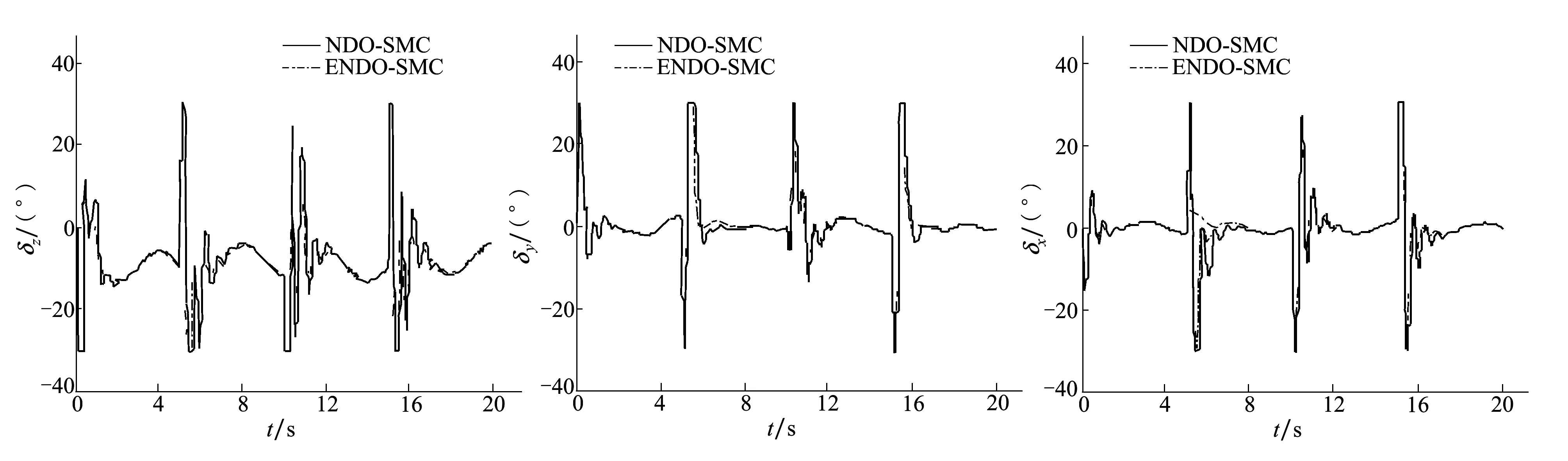
圖5 俯仰通道等效舵偏角 圖6 偏航通道等效舵偏角圖7 滾轉通道等效舵偏角

5 結 論

再入滑翔飛行器飛行速度高、飛行環境復雜多變、參數變化劇烈,系統存在較強的時變不確定性干擾,而傳統的非線性干擾觀測器均假設外部擾動變化緩慢或變化速率近似為零,限制了在再入滑翔飛行器上的應用。針對該問題,本文首先設計了一種擴張狀態的非線性干擾觀測器,可同時觀測干擾大小及其變化速率。在此基礎上,設計了一種具有干擾補償作用的新型滑模面,以及雙回路非奇異終端滑模控制律,有效解決了具有時變非匹配不確定性干擾的系統控制問題。以再入滑翔飛行器為算例的仿真結果表明,該方法能夠有效提高系統控制精度,控制指令更為平滑。

[1] 李菁菁,任章,宋劍爽. 高超聲速再入滑翔飛行器的模糊變結構控制[J]. 上海交通大學學報, 2011,45(2):295-300

LiJingjing,RenZhang,SongJianshuang.FuzzySlidingModeControlforHypersonicRe-EntryVehicles[J].JournalofShanghaiJiaotongUniversity, 2011,45(2): 295-300 (inChinese)

[2]XuH,MirmiraniMD,IoannouPA.AdaptiveSlidingModeControlDesignforaHypersonicFlightVehicle[J].JournalofGuidance,Control,andDynamics, 2004, 27(5): 829-838

[3]LianBH,BangH,HurtadoJE.AdaptiveBacksteppingControlBasedAutopilotDesignforReentryVehicle[C]∥ProcAIAAGuidanceNavigationandControlConfandExhibit, 2004, 1210

[4]HallCE,ShtesselYB.SlidingModeDisturbanceObserver-BasedControlforaReusableLaunchVehicle[J].JournalofGuidance,Control,andDynamics, 2006, 29(6): 1315-1328

[5]KoosunLee,JuhoonBack,IckChoy.NonlinearDisturbanceObserverBasedRobustAttitudeTrackingControllerforQuadrotorUAVs[J].InternationalJournalofControlAutomationandSystems, 2014:12(6):1266-1275

[6]YangJun.NonlinearDisturbanceObserverBasedRobustFlightControlforAirbreathingHypersonicVehicles[J].IEEETransonAerospaceandElectronicsSystems, 2013:49(2):1263-1275

[7]YangJun,LiShihua,YuXinghuo.Sliding-ModeControlforSystemswithMismatchedUncertaintiesviaADisturbanceObserver[J].IEEETransonIndustrialElectronics, 2013, 60(1):160-169

[8] 卜祥偉,吳曉燕,陳永興,等. 非線性干擾觀測器的高超聲速飛行器自適應反演控制[J]. 國防科技大學學報, 2014,36(5):44-49

BuXiangwei,WuXiaoyan,ChenYongxing,etal.AdaptiveBacksteppingControlofHypersonicVehiclesBasedonNonlinearDisturbanceObserver[J].JournalofNationalUniversityofDefenseTechnology, 2014, 36(5):44-49 (inChinese)

[9] 郭超,梁曉庚,王俊偉. 基于非線性干擾觀測器的攔截彈動態逆控制[J]. 系統工程與電子技術,2014,36(11):2259-2265

GuoChao,LiangXiaogeng,WangJunwei.NonlinearDisturbanceObserver-BasedDynamicInverseControlforNearSpaceInterceptor[J].SystemEngineeringandElectronics, 2014,36(11):2259-2265 (inChinese)

[10] 于靖,陳謀,姜長生. 基于干擾觀測器的非線性不確定系統自適應滑模控制[J]. 控制理論與應用, 2014,31(8):993-999

YuJing,ChenMou,JiangChangsheng.AdaptiveSlidingModeControlforNonlinearUncertainSystemsBasedonDisturbanceObserver[J].ControlTheory&Applications, 2014,31(8):993-999 (inChinese)

[11]GinoyaDivyesh,ShendgePD,PhadkeSB.SlidingModeControlforMismatchedUncertainSystemsUsinganExtendedDisturbanceObserver[J].IEEETransonIndustrialElectronics, 2014, 61(4):1983-1992

[12] 蒲明,吳慶憲,姜長生,等. 新型快速Terminal滑模及其在近空間飛行器上的應用[J]. 航空學報,2011,32(7):1283-1291

PuMing,WuQingxian,JiangChangsheng,etal.NewFastTerminalSlidingModeandItsApplicationtoNearSpaceVehicles[J].ActaAeronauticaetAstronauticaSinica, 32(7):1283-1291 (inChinese)

[13]YuShuanghe.ContinuousFinite-TimeControlforRoboticManipulatorswithTerminalSlidingMode[J].Automatica, 2005:41 1957-1964

[14]CybenkoG.ApproximationbySuperpositionsofaSigmoidalFunction[J].MathematicsofControl,SingnalsandSystems, 1989, 2(4): 303-314

Extended Disturbance Observer Based Terminal Sliding Mode Control for Reentry Vehicles

Zhou Jun, Zhao Jinlong

(Institute of Precision Guidance and Control,Northwestern Polytechnical University,Xi′an 710072,China)

This paper presents an extended nonlinear disturbance observer and novel double loop nonsingular terminal sliding mode control for reentry vehicles with time-varying unmatched disturbance. Firstly, the Lyapunov theorem is employed to design the extended nonlinear disturbance observer, where the state variables are extended to observe the disturbances and their changing rates simultaneously. The motion of reentry vehicle is separated into inner loop of angle and outer loop of angular rate, and a nonsingular terminal sliding mode control laws based on novel sliding mode is developed. The disturbance can be efficiently compensated and the tracking error is guaranteed to converge to zero in finite time. Simulation results and comparisons illustrate the effectiveness of the control strategy.

nonlinear disturbance observer; reentry vehicles; nonsingular; terminal sliding mode control

2016-04-02

國家自然科學基金(61473226)資助

周軍(1966—)，西北工業大學教授，主要從事飛行器先進制導與控制技術研究。

V438

A

1000-2758(2016)05-0817-06