基于局部概率可靠度的信息趨向源搜索方法

宋程, 賀昱曜, 楊盼盼, 雷小康

1.西北工業大學 航海學院, 陜西 西安 710072; 2.長安大學 電子與控制工程學院, 陜西 西安 710064 3.西安建筑科技大學 信息與控制工程學院, 陜西 西安 710055

?

基于局部概率可靠度的信息趨向源搜索方法

宋程1, 賀昱曜1, 楊盼盼2, 雷小康3

1.西北工業大學 航海學院, 陜西 西安 710072; 2.長安大學 電子與控制工程學院, 陜西 西安 710064 3.西安建筑科技大學 信息與控制工程學院, 陜西 西安 710055

信息趨向搜索方法能夠實現對稀疏線索源的有效搜索，但在局部線索稠密或近源區域存在趨近效率降低及局部自陷問題。為有效引導機器人向高信息區域運動以趨近源，提出了一種基于局部概率可靠度的信息趨向搜索方法。該方法引入一個與線索捕獲與否相關的局部概率可靠度，通過調節局部概率擾動對信息熵下降方向的影響，實現在線索稠密和近源區域的高效趨近。仿真結果表明，提出的基于局部概率可靠度的信息趨向方法能明顯提升搜索性能，且可有效逃脫局部自陷。

信息熵；稀疏線索；源搜索；局部自陷；信息趨向

近年來，利用稀疏線索和局部信息來搜索追蹤目標日益受到機器人領域研究者的關注[1-2]。利用機器人攜帶傳感器自主探測和發現目標(源)釋放的線索——化學物質、光、熱等, 進而追蹤此類線索至其源頭位置，是一種搜尋目標(源)的有效手段，其在事故救援、泄露檢查[3]、污染源搜尋[4]等方面有著十分廣闊的應用前景。

通常在流體環境中，目標釋放的線索被撕裂成煙絲或碎片狀，導致其檢測間斷和稀疏，無法獲得較為穩定的濃度梯度，對搜索者追蹤源頭帶來了嚴峻的挑戰。然而在自然界中，許多動物利用稀疏的氣味線索能夠在復雜的環境中尋找食物、配偶、巢穴。例如，雄蛾利用觸角在幾百米外就可以嗅到雌蛾釋放的信息素，從而確定雌蛾位置[5]。鯊魚可以嗅出濃度只有百萬分之一的血腥味，對數公里外的獵物進行追捕[6]。動物在稀薄氣味線索環境下的嗅覺溯源能力為機器人搜索釋放源提供了參考和啟發。

隨著信息論成功解釋了很多生物現象，研究者認為“信息”是許多生物嗅覺溯源行為的底層驅動機制[7]。Vergassola等[8]從信息論角度研究嗅覺行為機理，首次提出了以信息趨向性(infotaxis)獲取最大信息增益的源搜索策略(亦稱為信息熵決策)，成功地揭示了嗅覺溯源現象。Zhang[9]和Voges[10]對信息趨向性方法和常規的嗅覺行為模仿方法進行了定量比較分析，發現信息趨向性方法在湍流和噪聲環境中的搜索效率優于嗅覺行為模仿方法。Rodriguez等[11]進一步指出，信息趨向性方法對噪聲和湍流環境具有良好的魯棒性。最近，Martinez和Moraud等[12-13]發現信息趨向性的搜索路徑類似于雄蛾追蹤雌蛾的路徑軌跡，這在一定程度上印證了信息趨向性方法符合生物嗅覺溯源行為的機理。

雖然信息趨向性方法非常適用于線索稀疏情形下源搜索，在搜索效率上表現出比現有基于行為的方法以及基于模型的方法更為優越的性能[10,12]，并且在路徑形態上更接近于自然界中生物的溯源嗅覺行為路徑。但是，該方法存在固有缺陷，即在局部線索稠密或近源區域的搜索性能卻不盡理想[11]。實驗表明，在局部線索稠密或近源區域的趨近效率低下，搜索路徑存在大量的折轉，并可能發生局部自陷問題。Voges等[10]指出信息趨向性搜索策略在近源區域趨近率低下的原因在于熵降方向發生頻繁轉變增加了許多橫向運動而非逆風運動，致使趨近效率降低。為了克服這一缺陷，Masson等[14]加入了最大似然行為這一生物重要的認知方式，以自由能做為決策手段，避免了自陷行為。但是，該方法基于近似貝葉斯后驗概率，且依賴于犧牲搜索效率的參數選擇。Ristic等[15]將巴氏距離結合到信息趨向策略中，有效提高了趨近效率，但巴氏距離的引入急劇增加了計算量。

本文在分析源趨近過程中源位置估計概率遷移對期望信息梯度影響的基礎上，分析了經典信息趨向性方法(infotaxis)存在的不足，指出了一種基于局部概率可靠度的信息趨向源搜索方法(R-infotaxis)。通過引入局部概率可靠度，充分發揮信息熵在線索稠密和近源區域的引導作用，得到更為準確的信息熵下降方向，使經典信息趨向方法中搜索與利用的平衡更傾向于搜索。通過在平均路徑長度、趨近效率、信息收集速率等方面與經典信息趨向性方法的對比分析, 驗證了所提方法的可行性和有效性。

1 問題描述

利用機器人進行源搜索任務，需構建包含濃度、風速、位置等信息的源線索空間分布的擴散模型和傳感器檢測模型。源搜索的基本思路是根據機器人的實時運動和檢測到的信息，結合上述模型采用貝葉斯推理得出源位置的概率分布。本節對其中涉及的基本模型加以介紹。

1.1 擴散模型

在真實環境中，擴散的化學物質分子被湍流所擾亂，結構不規則。在此，采用湍流環境下常用的統計氣體擴散模型刻畫線索不連續和隨機的分布特性。該模型將捕獲線索視為粒子遇碰，以遇碰概率描述線索的空間分布。若設搜索者在位置r處對源r0=(x0,y0)釋放的線索進行捕獲,則在二維空間中,位置r處的線索捕獲率(采樣率)R(r|r0)為[8]

(1)

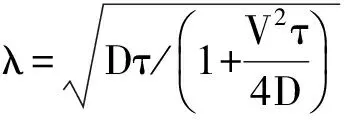
1.2 檢測模型

對于在流體中擴散的化學物質,傳感器所檢測到的濃度在時間和空間上存在劇烈波動,其瞬間濃度梯度易出現突變。為了避免具體濃度數值的不準確性,本文采用二值檢測傳感器[16]對采樣濃度進行處理,即當傳感器的檢測濃度數值大于某一閾值便認為捕獲線索,感知結果為“1”。受此作用,在位置r的線索捕獲近似為一個泊松過程。因此,在有限時間間隔Δt內,傳感器在位置r處捕獲z次線索服從泊松分布,其概率為

(2)

式中,λp=R(r|r0)·Δt,其與線索捕獲率成正比。

1.3 貝葉斯推理

由于線索捕獲率與離源距離有關,在機器人軌跡Γt上發生的檢測序列[rt1,rt2,…,rtn]就攜帶了源位置信息。可利用貝葉斯推理從軌跡Γt中得到源位置r0概率分布Pt(r0)。定義軌跡Γt的可能性為

(3)

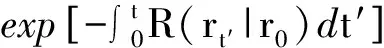
基于此,機器人經歷軌跡Γt后源位置的貝葉斯后驗概率Pt(r0|Γt)為[8]

(4)

若不存儲全部路徑信息,則貝葉斯后驗概率Pt(r0|Γt)遷移為

(5)

式中,η為機器人在時間間隔Δt內捕獲線索的次數,Zt+Δt為歸一化常數。

2 信息趨向性方法

傳統源搜索策略包括基于濃度的化學趨向性方法、基于風向的風趨向性方法等。然而在湍流環境下,由于局部濃度突變及風向不穩定,使得化學趨向性和風趨向性方法搜索效率低下甚至不可行。信息趨向性方法將濃度、風向、風速等融合為“信息”這一單一要素作為搜索者實施搜索的線索,能有效克服湍流環境下的源搜索問題[13]。

在信息趨向性方法中,信息熵被作為衡量源位置不確定性的測度。信息熵的變化被作為一種瞬時勢場,驅使機器人向熵降最快的方向移動,當熵值減為0時,即不確定性消失,則認為找到源。

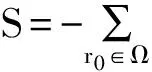
(6)

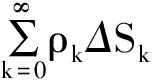
基于(6)式得出的熵減量,選取搜索者當前所有可行方向中下降幅度最大者作為搜索者最佳移動方向,如此往復,直到源被確認。因而信息趨向性方法的本質是將源位置的搜索過程轉換為信息源的趨近過程。這一策略尤其適用于稀疏線索環境,然而,該方法由于局部頻繁捕獲引起探索與利用失調導致在線索稠密或近源區域產生趨近效率下降和自陷等問題。下文將對此予以討論并給出改進方案。

3 基于局部概率可靠度的信息趨向搜索方法

記搜索者的當前位置為rt,候選的行進方向為rj={·,→,↑,←,↓},分別對應于原處、左、右、前、后5個方向。在理想情況下,(6)式中的A項僅在源位置后驗估計概率較大且準確可靠時發揮作用。實際源搜索過程則不然,局部源存在概率Pt(rj)的擾動影響A項在信息熵降的比重。

首先考察搜索者當前位置rt處捕獲線索與否對源存在概率Pt(rj)影響,根據(5)式可得

(7)

該式表明Pt(rj) 受rt處是否捕獲線索的影響。具體而言,(1)若在rt處未能捕獲線索,Pt(rj) 在Pt-Δt(rj)的基礎上減小,即源在rj處的可能性減小。(2)若在r處捕獲到線索,Pt(rj) 在Pt-Δt(rj)的基礎上增大,即源在rj處的可能性增大。

在(6)式中,候選方向rj處源位置后驗概率分布Pt(rj)起到調節探索(即B項)與利用(即A項)在信息梯度中相對權重的作用。然而,由(7)式可知,搜索過程中Pt(rj)會存在以下3種擾動情況:

1) 捕獲線索與否是個隨機過程,其對于候選運動方向的后驗概率影響很大,尤其是捕獲線索后,Pt(rj)突然增大。

2) 若機器人在鄰近位置相繼捕獲線索,由此產生的疊加效應使得Pt(rj)擾動加劇。這一情況在線索稠密和近源區域表現尤為突出。

3) 在捕獲線索較少時,路徑Γt未包含足夠的源位置信息,導致(5)式估計出的Pt(rj)不可靠。

由于上述后驗概率Pt(rj)的擾動存在,使利用項A在信息熵降中比重失調。尤其是當鄰近位置相繼捕獲線索時,Pt(rj)出現突變增大,導致A項在ΔES(rt→rj)中的權重增加,致使全局的信息熵被局部不可靠概率干擾,機器人在局部選擇非最佳的前進方向。因而,經典信息趨向性方法容易產生自陷和趨近效率低下問題。

3.1 局部概率可靠度

鑒于信息趨向方法中的“利用”是以最大似然作為實現方式。Pt(rj)表現了最大似然的作用強度,其在線索稠密條件下的突然增大會導致局部最大似然的“過度”作用。事實上,貝葉斯推理后驗概率分布梯度穩定性決定了最大似然的可靠程度:遷移變化劇越烈(即梯度越不穩定),采用最大似然趨向源位置的可靠度越低;反之,越平緩,梯度越穩定,可靠度越高。通過前面分析已知,當線索稠密或近源區域頻繁捕獲線索,Pt(rj)遷移變化劇烈;當脫離這個區域,Pt(rj)遷移變化平緩。據此規律,考慮引入局部概率可靠度加以克服。

記當前時刻至搜索者前次捕獲線索的時間間隔為tlast,局部概率可靠度β是關于tlast的函數。當搜索者在位置rt處捕獲到線索時,候選方向rj的源分布概率Pt(rj)突然遷變,此時可靠度β=0,隨著時間tlast的增加,局部概率不發生突然遷變,可靠度β隨之恢復到1。據此,將β設計成如下形式

(8)

式中,a>0為調節參數。該式實現可靠度在線索捕獲時引起局部概率擾動情況下動態切換過程。

3.2 改進的信息趨向性方法

基于前文分析及相關定義,本文提出一種基于局部概率可靠度的信息趨向方法。該方法的下一步移動到周圍柵格(或者靜止不動)導致的熵的減小量為

(9)

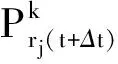
相較于(6)式、(9)式得到的信息熵減能夠消除局部概率Pt(rj)擾動的影響,充分發揮信息熵這一全局量的引導作用,得到更為準確的信息梯度方向。當機器人頻繁捕獲線索時,β的引入減弱局部概率擾動對信息梯度影響;當脫離局部多次捕獲區域(即線索稠密和近源區域),局部概率恢復對信息梯度影響。這樣可以避免由局部概率擾動引起的趨近效率降低和局部自陷問題。

Infotaxis方法包含“熵減期望”和“最大似然”兩種引導策略。其中熵減期望為探索的實現方式,最大似然是利用的實現方式。探索與利用的平衡是以熵減期望和最大似然的權衡為準則。熵減期望引導搜索向著期望獲得更多線索的方向(概率集中的區域),而最大似然趨向估計的源分布概率最大的位置。與經典信息趨向性方法相比,(9)式的最大不同在于通過局部概率可靠度減弱頻繁捕獲線索時最大似然的作用。可靠度β在信息趨向方法中用以調整最大似然和信息熵梯度的平衡關系,在Pt(rj)突然增加時不至于使最大似然作用過度。

另外值得注意的是,本文所提方法與經典信息趨向性方法在源確認方面認知不同。在經典信息趨向性方法中,機器人沿熵降的方向行進,信息熵為0時源被確認,這是信息論視角角下的源確認問題。然而我們研究發現到達源位置時的信息熵并不為零。因此,對于機器人而言,到達即為確認(源確認方法見文獻[17])而非信息論角度下的確認,這是經典信息趨向方法認識上的偏差,其由(6)式中A項作用過強導致。在本文所提方法中,利用局部概率可靠度使捕獲線索頻繁時傾向于B項,即強化探索的作用,更有利于趨近源位置。

3.3 算法流程

基于局部概率可靠度的信息趨向性方法的具體步驟如下:

Step1 初始化后驗概率Pt(r0)和信息熵St;

Step2 計算在每個rj處期望捕獲線索次數h(rj),h(rj)=Δt∫Pt(rx)R(rj|rx)drx。進而計算在rj處Δt時間內捕獲k次線索的概率ρk(rj)=hke-h/k!;

Step4 計算可靠度β;根據公式(9)計算由位置rt移動到rj可能引起的信息熵變化ΔES(rt→rj),選擇其中ΔES(rt→rj)變化最大的rj作為最佳移動位置;

Step5 記錄在t時刻位置rt移動到t+Δt時刻位置rj的時間Δt內,捕獲的線索數量η=0,1,2,…;

Step6 根據公式(5)更新后驗概率Pt(r0)為Pt+Δt(r0)以及相應的信息熵由St更新為St+Δt;

Step7 返回step2,直至到達源所在位置結束。

4 仿真分析

本節通過數值仿真實驗,分析比較本文所提R-infotaxis方法與經典infotaxis方法利用稀疏線索源搜索性能,驗證所提方法的可行性和有效性。

4.1 仿真環境

實驗中采用Balkovsky的格構煙羽模型生成煙羽,實現方法詳見文獻[18],并考慮增加了氣味粒子的短暫壽命。實驗的仿真參數設置如下[9]:粒子擴散率D=1,粒子生命周期τ=50,源釋放率Q=1,平均風速V=1,傳感器的測量半徑α=0.5。搜索空間為100×100,源的位置隨機指定。可靠度β的計算式(8)中參數a=100。所有數值仿真在MATLAB中進行。

4.2 分析指標

為了便于分析和評價機器人的搜索性能,定義以下一組指標:

1) 路徑長度:機器人完成搜索任務所經歷的軌跡長度,即從起始位置到達源所在位置的歐式距離,是衡量搜索方法優劣的基本指標。

2) 趨近效率:逆風運動在搜索過程中所有運動中所占的比重。機器人在搜索過程中運動包括橫越運動(traverse)、逆風運動(upwind)和順風運動(downwind)3種運動形式。其中,逆風運動對源搜索最為有效,可用于評價搜索運動的有效性(路徑質量)。

3) 信息收集速率:源搜索過程中信息熵時間演化曲線的斜率。源搜索任務可視為趨向信息源的過程,源趨近過程中的線索捕獲即為信息收集。信息熵的變化可以實時反映這一過程的進度。

4.3 仿真結果

為了直觀展示R-infotaxis的源搜索性能,圖1給出了一組不同起始位置下R-infotaxis方法的典型搜索路徑。為了便于比較,圖中同時給出了相同條件下經典infotaxis方法的搜索路徑。可以看出,從不同的起始位置出發,2種方法均能完成源搜索任務,但兩者的搜索路徑存在顯著差異。(1)路徑細節方面,經典infotaxis方法的搜索路徑曲折,存在較多折轉,且折轉多發生于線索剛捕獲時;R-infotaxis的路徑更為平直,尤其在近源區域,其路徑徑直奔向源位置。(2)經典infotaxis路徑中多次出現局部重復搜索的自陷問題(如圖1a)所示)。由此可見,R-infotaxis的搜索表現好于infotaxis。

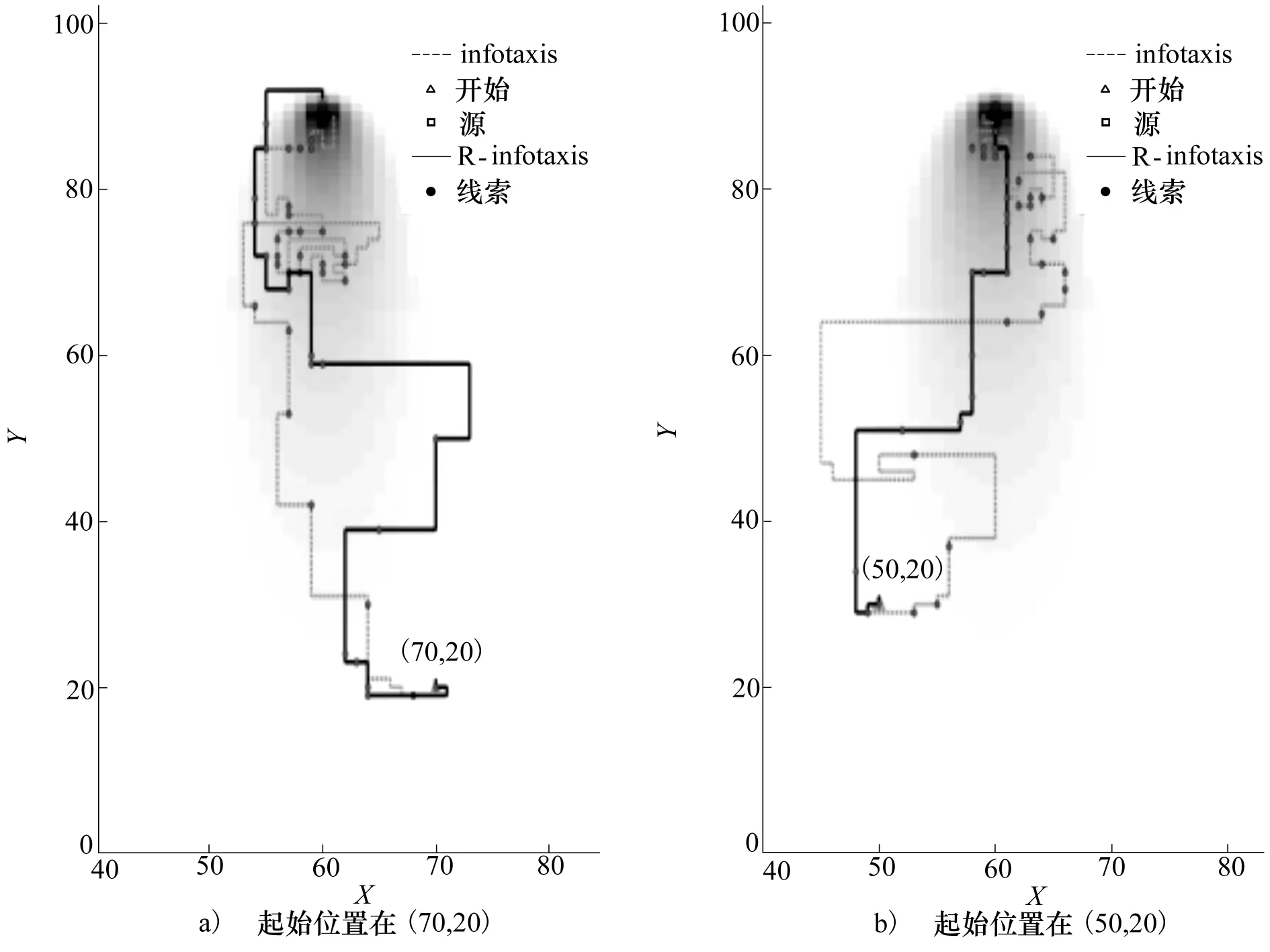
圖1 經典infotaxis方法與R-infotaxis方法的搜索路徑比較

圖2進一步展示了機器人搜索的動態過程,圖中灰色部分顯示源位置的后驗概率Pt(r0),其灰度反映了源存在概率的高低。從中可以看出:(1)隨著機器人運動不斷捕獲線索,源位置估計概率發生遷移,最終高概率區域涵蓋源所在位置;(2)infotaxis方法在相繼捕獲線索時,鄰近區域概率突增(灰度加深,如圖2a)～圖2c)所示),容易誘發局部回轉甚至引發自陷問題;反觀R-infotaxis方法即便在連續捕獲線索的情況下基本不受局部概率增加的影響,不發生折轉,傾向于前向運動(如圖2d)～圖2f)所示)。

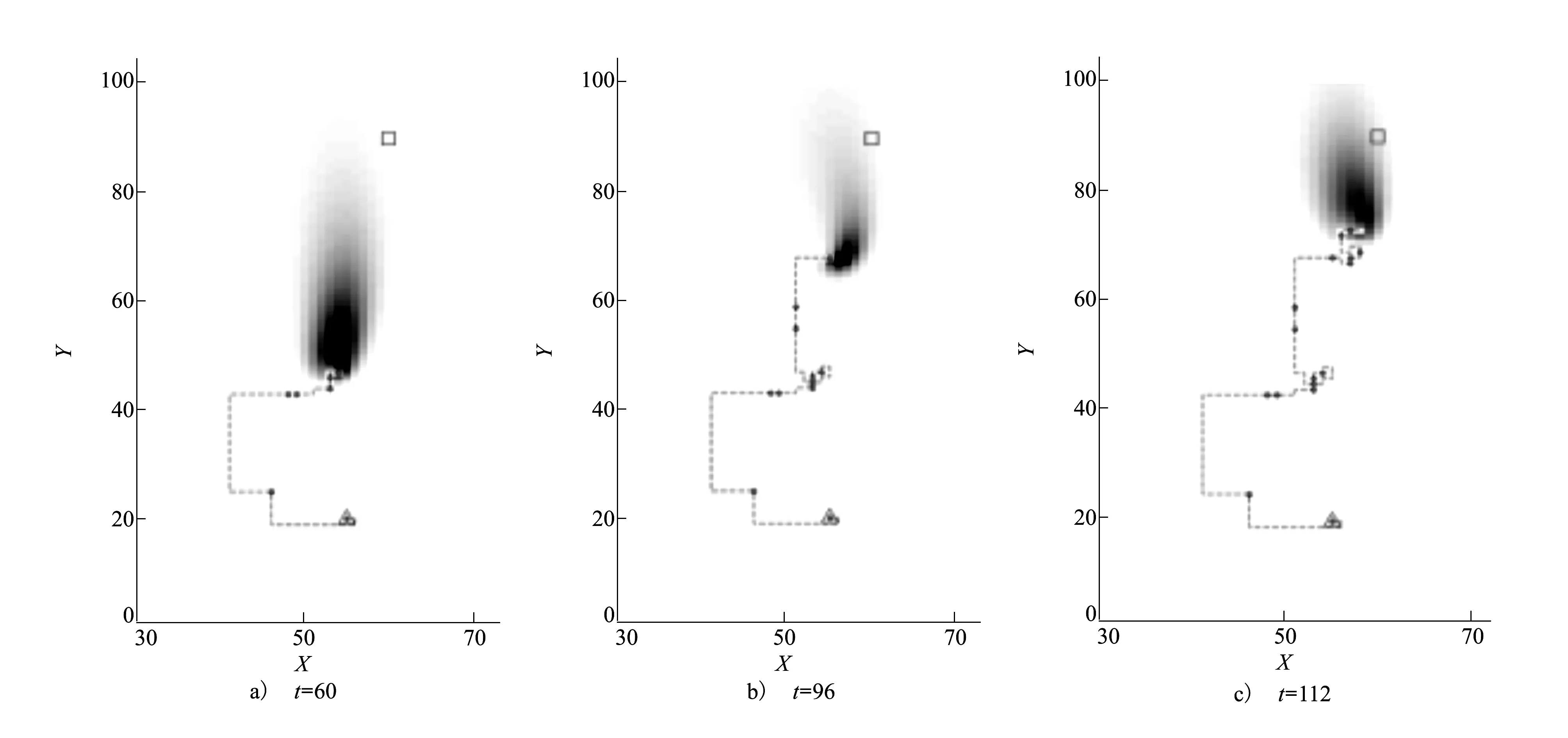
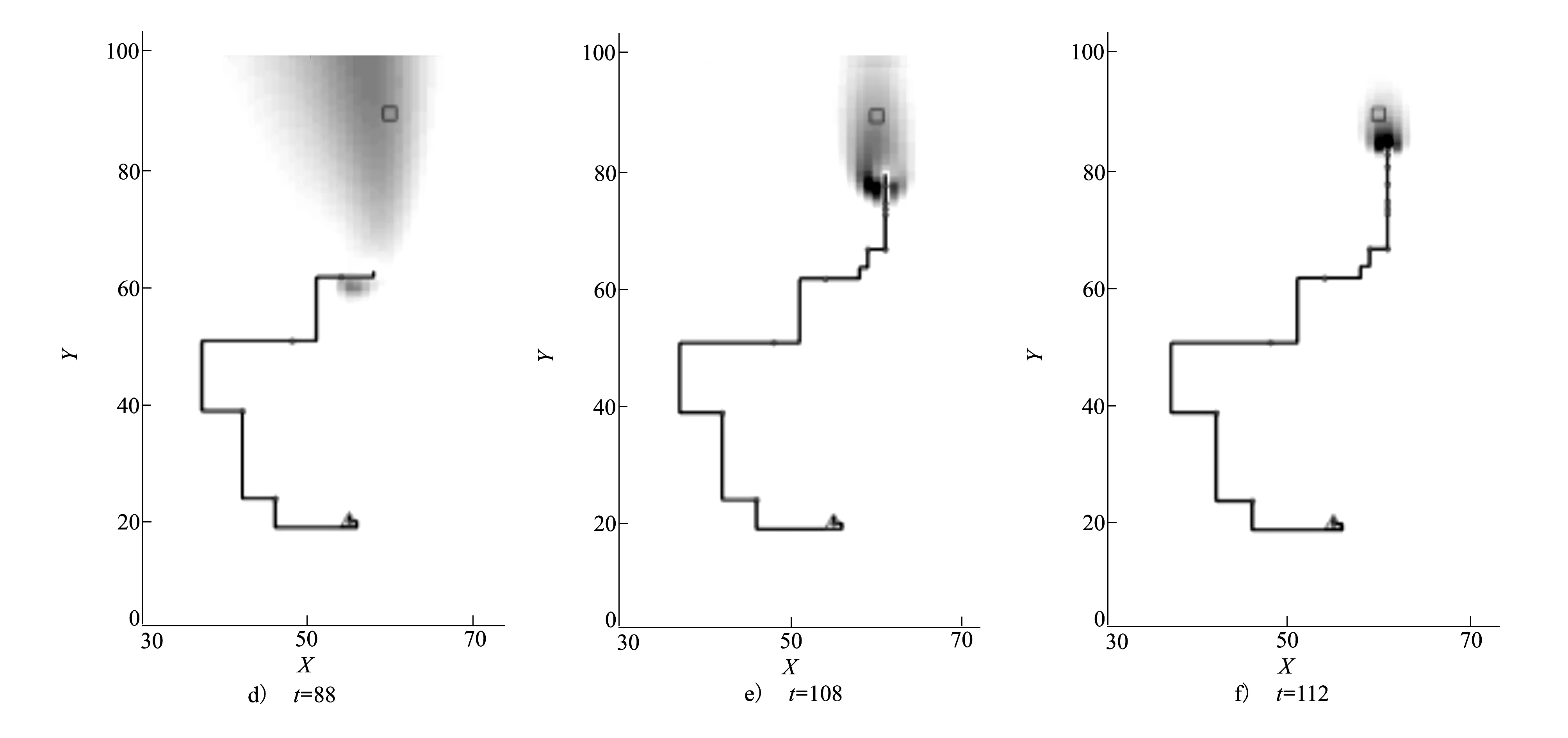
圖2 infotaxis(a～c)和R-infotaxis(d～f)搜索的動態過程

上述仿真實例定性地驗證了R-infotaxis方法對經典infotaxis方法的搜索性能提升。下面利用Monte Carlo仿真實驗，基于路徑長度、趨近效率、信息收集效率等量化指標對兩者做進一步比較實驗研究。為減少誤差，下述所有結果均取50次獨立仿真的平均值，仿真條件如圖1a)所示。

1) 路徑長度

表1給出了路徑長度統計結果，可以看出，(1)本文提出的R-infotaxis方法平均路徑長度相對于經典infotaxis方法縮短了約20%；(2)在最短路徑方面，較經典方法可縮短近28%；(3)在最長路徑方面，R-infotaxis較經典方法優勢不甚顯著，這表明R-infotaxis能以更短路徑完成源搜索任務。

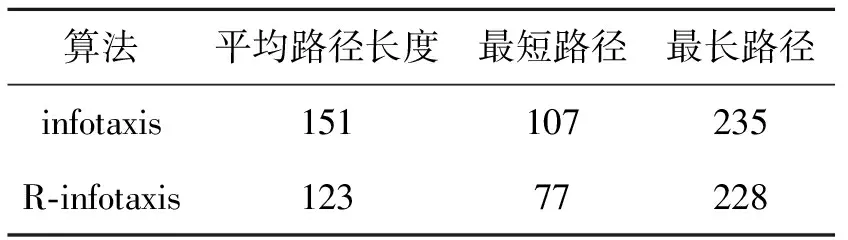
表1 搜索路徑長度比較

2) 趨近效率

圖3給出了搜索路徑中逆風、橫越、順風等運動成分(依據折轉方向統計)的占比分布。可以看出：(1) 3種運動中逆風運動占比最高，顯示出整體徑向趨近于源(見圖1a))；橫越風運動占比適中，有利于探索范圍的擴展；順風和停留運動占比最少，可減少無效運動。(2) 相較經典infotaxis而言，R-infotaxis方法提高了逆風運動的比重，由51.3%提高到62.4%， 這是搜索路徑質量得以提高的主要因素；橫越風運動由39.5%降到34.3%，無效運動也降到極低的3.3%， 這些減少可一定程度上減少回轉。究其原因，這是由于可靠度 的引入，使得前向性得到加強，搜索者傾向于逆流而上，同時保持一定的橫越風運動，以保持橫向搜索能力。

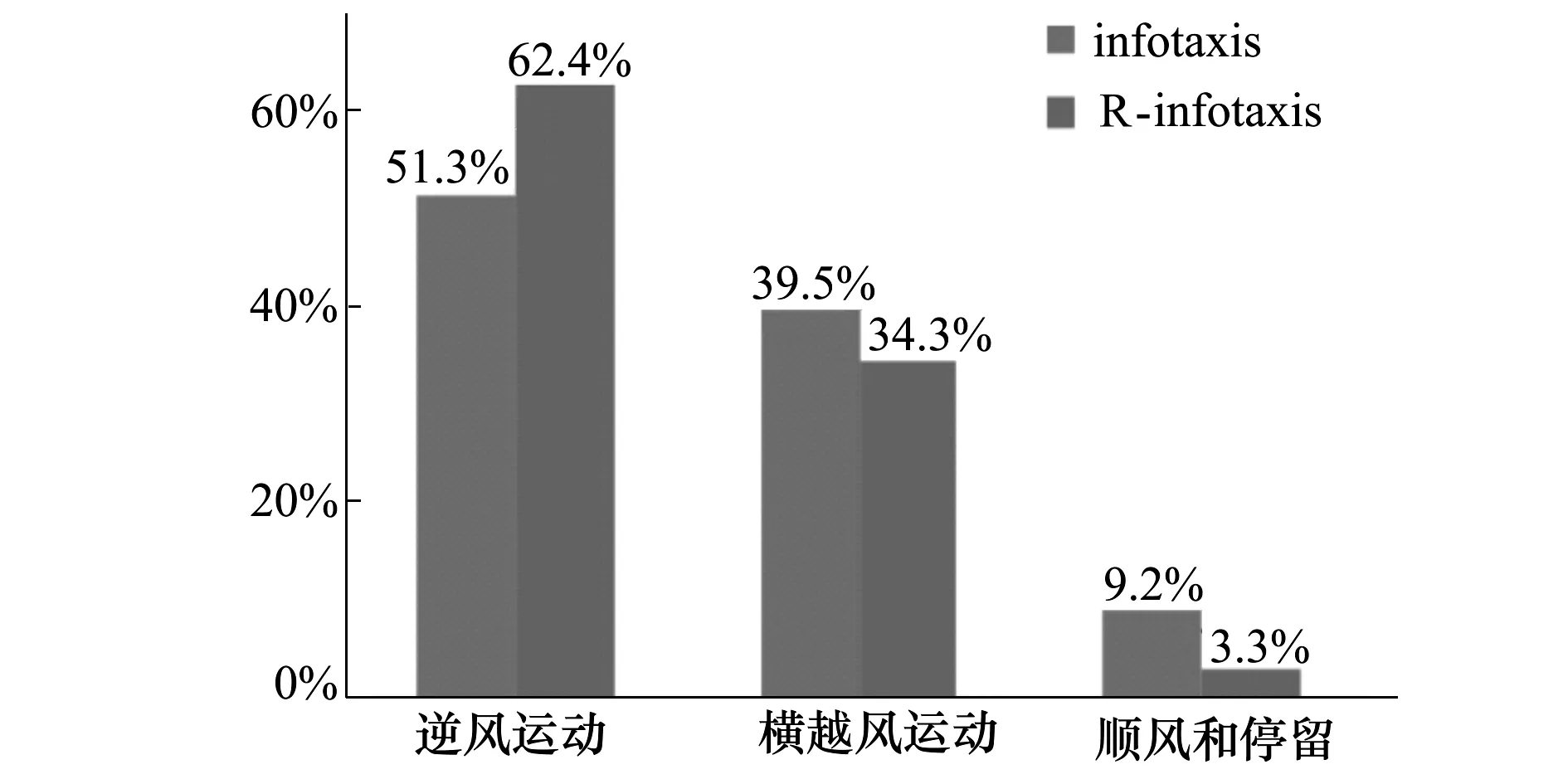
圖3 運動成份對比

3) 信息收集速率

為了量化分析R-infotaxis方法與經典infotaxis方法的信息收集速率的差異，圖4給出了圖1a)所示R-infotaxis和infotaxis搜索過程對應的信息熵時間演化曲線和相應的線索捕獲量。

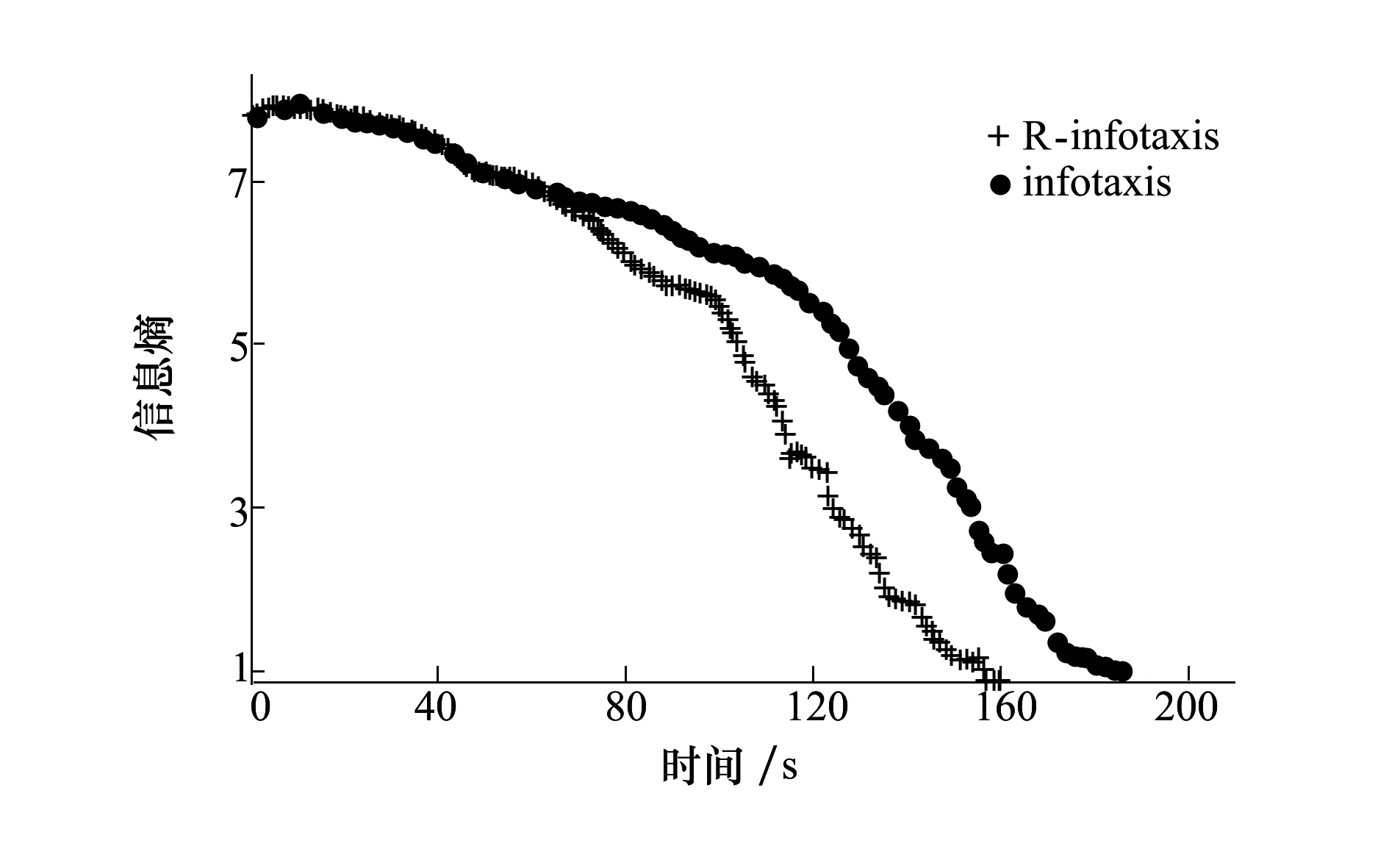
圖4 信息熵變化曲線

從中可以看出，整個搜索過程可以明顯分成2個階段：(1)初始階段(0～80)，兩者曲線基本重合，這表明在線索稀疏情況下信息收集速率無較大差異。(2)后期階段(>80)，R-infotaxis的熵曲線下降趨勢明顯快于infotaxis，這表明R-infotaxis具有更快的信息收集速率，即趨向信息源的進程更快。出現上述情形的原因在于：初始階段線索稀疏，R-infotaxis方法退化為經典infotaxis方法，故兩者的信息熵時間演化曲線基本重合；之后，隨著線索捕獲逐漸增多，R-infotaxis方法中最大似然作用減弱，機器人繼續沿著期望熵降方向行進，而infotaxis方法受局部最大似然作用較強，局部折轉增加，導致其信息收集速率低于R-infotaxis方法。總體而言，本文提出的R-infotaxis方法擁有更高的信息收集速率。

綜合以上多方面對比，本文提出的R-infotaxis方法較經典infotaxis方法的搜索性能更為優良，其搜索路徑更短、趨近效率更高、信息收集速率更快。

5 結 論

針對經典infotaxis方法在線索稠密和近源區域存在趨近效率低下及自陷的問題，通過分析得出了局部概率擾動是局部最大似然過渡作用，導致趨近效率降低。據此引入了局部概率可靠度，用以調整在線索頻繁捕獲時最大似然作用強度。進而，提出了一種新的基于概率可靠度的信息趨向方法，從而保證以良好的趨近效率趨近源。最后實驗比較了本文提出的基于概率可靠度的信息趨向方法和經典信息趨向方法的搜索性能，分別考察了平均路徑長度、信息收集速率、趨近效率。結果表明，基于局部概率可靠度的信息趨向方法在這些方面的表現優于經典信息趨向方法，更適應于局部稠密和稀疏等復雜的環境。

[1] Ishida H, Wada Y, Matsukura H. Chemical Sensing in Robotic Applications: A Review[J]. IEEE Sensors Journal, 2012, 12(11): 3163-3173

[2] Lilienthal A J, Loutfi A, Duckett T. Airborne Chemical Sensing With Mobile Robots[J]. Sensors, 2006, 6(11): 1616-1678

[3] Ishida H, Nakayama G, Nakamoto T, et al. Controlling a Gas/Odor Plume-Tracking Robot Based On Transient Responses Of Gas Sensors[J]. IEEE Sensors Journal, 2005, 5(3):537-545

[4] Woodfin R L. Trace Chemical Sensing of Explosives[M]. John Wiley & Sons, 2006

[5] Vickers N J. Mechanisms of Animal Navigation in Odor Plumes[J]. The Biological Bulletin, 2000, 198(2): 203-212

[6] Gardiner J M, Atema J. The Function of Bilateral Odor Arrival Time Differences in Olfactory Orientation of Sharks[J]. Current Biology, 2010, 20(13): 1187-1191

[7] Linsker R. Perceptual Neural Organization : Some Approaches Based on Network Models and Information Theory[J]. Annual Review of Neuroscience, 1990, 13(1): 257-281

[8] Vergassola M, Villermaux E, Shraiman I. “Infotaxis” As a Strategy for Searching without Gradients[J]. Nature, 2007, 445(7126): 406-409

[9] 張思齊, 崔榮鑫, 徐德民. 稀疏環境中信息趨向性搜索算法性能分析[J]. 機器人, 2013, 35(4): 432-438

Zhang S Q, Cui R X, Xu D M. Performance Analysis on The Infotaxis Algorithm for Searching in Dilute Environments[J]. Robot, 2013, 35(4): 432-438 (in Chinese)

[10] Voges N, Chaffiol A, Lucas P, et al. Reactive Searching and Infotaxis in Odor Source Localization[J]. Plos Computational Biology, 2014, 10(10):e1003861-e1003861

[11] Rodrguez J D, Gmez-Ullate D, Meja-Monasterio C. Limits on the Performance of Infotaxis under Inaccurate modelling of the Environment[J]. Eprint Arxiv, 2014, 1408(1873): 1-8

[12] Martinez D, Martin-Moraud E. Reactive and Cognitive Search Strategies for Olfactory Robots[J]. Neuromorphic Olfaction, 2013(5): 153-172

[13] Moraud E M, Martinez D. Effectiveness and Robustness of Robot Infotaxis for Searching in Dilute Conditions[J]. Frontiers in Neurorobotics, 2010, 4(4):1-8

[14] Masson J B. Olfactory Searches with Limited Space Perception[J]. Proceedings of the National Academy of Sciences, 2013, 110(28): 11261-11266

[15] Ristic B, Skvortsov A, Gunatilaka A. A Study of Cognitive Strategies for an Autonomous Search[J]. Information Fusion, 2016, 28(C):1-9

[16] Ristic B, Gunatilaka A, Gailis R. Achievable Accuracy in Gaussian Plume Parameter Estimation Using a Network of Binary Sensors[J]. Information Fusion, 2015, 25(32): 42-48

[17] Hayes A T, Martinoli A, Goodman R M. Distributed Odor Source Localization[J]. IEEE Sensors Journal, 2002, 2(3): 260-271

[18] Balkovsky E, Shraiman B I. Olfactory Search at High Reynolds Number[J]. Proceedings of the National Academy of Sciences, 2002, 99(20): 12589-12593

An Infotaxis Strategy for Seeking a Dispersion Source Using Local Probabilistic Reliability

Song Cheng1, He Yuyao1, Yang Panpan2, Lei Xiaokang3

1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China 2.School of Electronic and Control Engineering, Chang′an University, Xi′an 710064, China 3.School of Information and Control Engineering, Xi′an University of Architecture and Technology, Xi′an 710055, China

Infotaxis search can effectively navigate the robot to a dispersion source using sporadic cues. But low efficiency and local self-trapping problems come out in the dense cues or near-source area for this method. After analyzing the causes of these problems, a novel infotaxis method based on a local probability reliability is proposed. In this method, a reliability factor related to cues capturing is introduced. It is used to adjust the influence of the local probability disturbance on the drop trend of information entropy. Through guiding the robot to high information zone, the dispersion source can be approached. The simulation results demonstrate that the proposed infotaxis method presents a good search performance in sparse and dense cues environment, which can also effectively escape from local self-trapping.

entropy, sporadic cues, source seeking, local self-trapping, infotaxis

2016-03-17

國家自然科學基金(61271143)資助

宋程(1987—), 西北工業大學博士研究生, 主要從事智能導航和控制研究。

TP273

A

1000-2758(2016)05-0843-08