兩類非對稱量子碼的構造
馬月娜, 馮曉毅, 蘇志忠, 劉楊2,
1.西北工業(yè)大學 電子信息學院, 陜西 西安 710072; 2.空軍工程大學 理學院, 陜西 西安 710051 3.空軍第一航空學院 訓練部, 河南 信陽 464000
?
兩類非對稱量子碼的構造
馬月娜1,2, 馮曉毅1, 蘇志忠3, 劉楊2,3
1.西北工業(yè)大學 電子信息學院, 陜西 西安 710072; 2.空軍工程大學 理學院, 陜西 西安 710051 3.空軍第一航空學院 訓練部, 河南 信陽 464000
通過分圓陪集確定出q2-元域上2個嵌套的BCH碼滿足Hermite對偶包含的條件;利用這些滿足Hermite對偶包含條件的本原BCH碼構造出兩類非對稱量子碼的參數,使構造出的碼具有較大的z-距離,而且其參數優(yōu)于已有文獻中的結論,從而提高了碼的糾錯能力。
非對稱量子碼;BCH碼;Hermite對偶包含;CSS構造法
量子糾錯碼在量子容錯計算與量子通信等量子信息處理中發(fā)揮著重要作用。然而在量子信息的傳輸過程中,由于傳輸信道的不同可導致比特錯誤σx和相位錯誤σz出現(xiàn)的可能性也不盡相同,于是,人們針對量子信道中錯誤類型的非對稱特征,提出了一種新的量子糾錯碼——非對稱量子糾錯碼[1-4]。q-元非對稱量子[[n,k,dz/dx]]q碼可以控制所有?(dx-1)/2」個比特錯誤和?(dz-1)/2」個相位錯誤。與此同時,可以檢測出dx-1個比特錯誤和dz-1個相位錯誤,因此dz和dx的取值決定了碼的檢錯和糾錯能力[5-8]。Ioffe和Mezard[5]根據比特錯誤和相位錯誤出現(xiàn)的不同頻率,以及對糾錯能力的不同要求,借鑒標準量子糾錯碼的構造方法,構造出了非對稱量子糾錯碼,使其具有更好的糾錯效率;Aly和Sarvepalli等[6-9]將標準量子糾錯碼的CSS構造法推廣到非對稱量子糾錯碼,利用非本原狹義BCH碼和RS碼構造出很多參數優(yōu)良的非對稱量子糾錯碼;在此基礎上,Wang Long等[10]將非加性標準量子碼的特性推廣到非對稱情形,建立了非對稱量子碼和經典糾錯碼之間的關系;Ezerman等[11-12]將CSS構造法加以推廣,給出CSS-like構造法,利用該方法和嵌套的自正交線性碼構造出一系列新的非對稱量子糾錯碼;La Guardia[13-15]利用兩類具有對偶包含關系的BCH碼構造出一系列二元和非二元的非對稱量子糾錯碼,這些碼的參數優(yōu)于已有的量子糾錯碼的參數。陳建章等人[16]利用常循環(huán)碼和非本原BCH碼構造出一些參數優(yōu)良的非對稱量子碼。
本文在m分別為2l+1(l≥1)和2l(l≥2)2種情況下,利用q2-元域上碼長為n=22m-1的本原狹義BCH碼構造兩類非對稱量子碼的參數,使構造出的非對稱量子碼的z-距離遠大于δmax,其中δmax=qm+1-q2+1(m=2l)和δmax=qm-1(m=2l+1)分別是對偶包含狹義BCH碼的最大設計距離。
1 預備知識
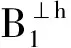
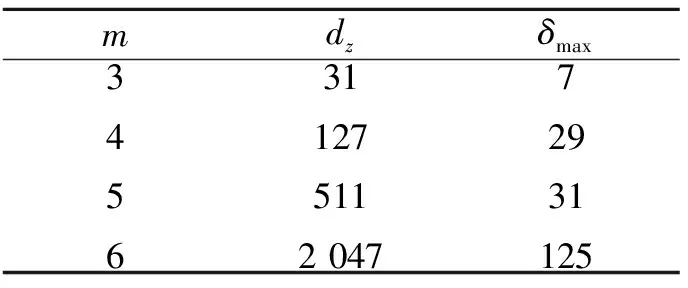
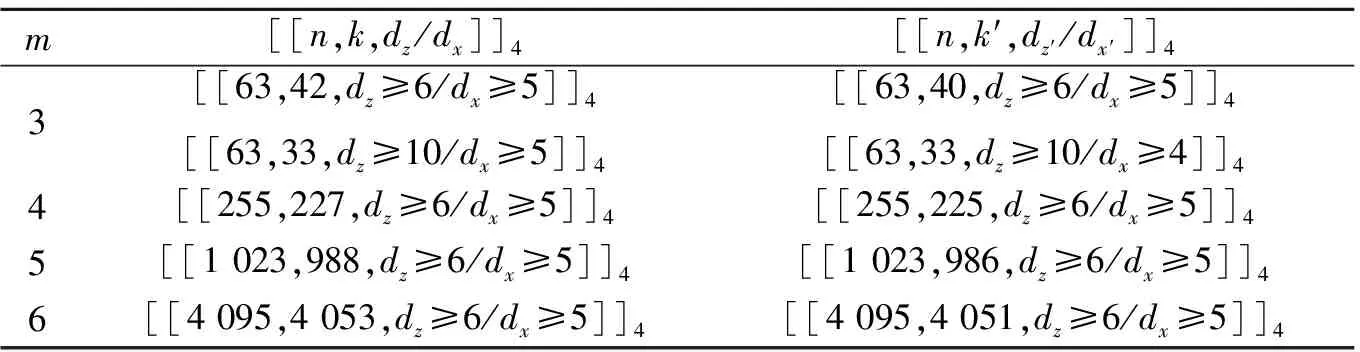
定義1 設q為素數的冪,n>1為正整數且gcd(n,q)=1。若x為正整數且滿足x 定義2 設Fq2為q2-元域,ξ為Fq2擴域上的n次本原單位根,若T=Cb∪Cb+1∪…∪Cb+δ-2=T[b,b+δ-2],以T為定義集合的、碼長為n的循環(huán)碼C叫做Fq2上的設計距離為δ的BCH碼。當n=q2m-1時C叫做q2-元本原BCH碼,否則叫做非本原BCH碼;如果b=1,C叫做狹義BCH碼,否則叫做非狹義BCH碼。 引理1 若gcd(n,q)=1,Fq2上的循環(huán)碼C的定義集合為T,則C⊥h?C當且僅當T∩T-q=Φ,其中T-q={n-qt(modn)|t∈T}。 文獻[12]將標準的CSS構造法推廣到滿足Hermite內積、跡Hermite內積和跡Euclide內積條件下的非對稱量子碼的構造中,給出了CSS-like(CSS-type)構造法,下述定理1.3就是構造滿足Hermite對偶包含條件下的非對稱量子碼的CSS構造法。 在以前的工作中,人們利用q-元域上2個嵌套的滿足Euclide對偶包含條件的BCH碼構造非對稱量子碼,得到很多參數優(yōu)良的非對稱量子BCH碼。然而利用q2-元域上滿足Hermite對偶包含條件的BCH碼構造非對稱量子碼,其構造結果大多局限于dz≤δmax,見文獻[13]。為了突破這一局限,本節(jié)討論m=2l+1和m=2l情況下,利用滿足Hermite對偶包含條件的2個碼長為n=22m-1的BCH碼構造非對稱量子碼的參數,并且使所得到的dz>δmax。 2.1 當m=2l+1(l≥1)時非對稱量子碼的構造 u=min{x|x∈T-q},v=max{y|y∈T-q},與文獻[19-21]相似,有如下引理1: 又因為 由此可知T⊥h至少包含u或者n-v-1個連續(xù)整數,因此δ(B⊥h)=max{u,n-v}。 下面定理3給出BCH碼滿足Hermite對偶包含的條件。 定理3 設n=22m-1,m=2l+1(l≥1)。 (3) 當1≤i≤l-1時,若δ1=22i+1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1-1,δ1<δ2≤24l-2i+2-1 或δ1=22i+1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=3·22i+1+1,δ1<δ2≤24l-2i+1-3, 證明 以(2)為例,令n=22m-1,m=2l+1(l≥1)。 同理可證(1)、(3)和(4)結論成立。 定理4 設n=22m-1,m=2l+1(l≥1)。 (1) 若i=0,當δ1=22i+1,δ1<δ2≤24l+1-1時,存在參數為[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非對稱量子碼; (2) 若1≤i≤l,當δ1=22i+1,δ1<δ2≤2·24l-2i+2-2 時,存在參數為[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非對稱量子碼; (3) 若1≤i≤l-1,當δ1=22i+1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1-1,δ1<δ2≤24l-2i+2-1 或δ1=22i+1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=3·22i+1+1,δ1<δ2≤24l-2i+1-3,存在參數為[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非對稱量子碼; (4) 若i≤l,當δ1=22i+1-2,δ1<δ2≤3·22l+1-1 或δ1=22i+1-1,δ1<δ2≤22l+2-1時,存在參數為[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非對稱量子碼。 證明 以(2)為例,設n=22m-1,m=2l+1(l≥1)。 同理可得(1)、(3)和(4)結論成立。 2.2 當m=2l(l≥2)時非對稱量子碼的構造 本節(jié)將構造一類碼長為n=24l-1(l≥2)的非對稱量子碼的參數。和定理3類似,首先給出這些滿足Hermite對偶包含條件的BCH碼的最大設計距離,見定理4。 定理4 設n=22m-1,m=2l(l≥2)。 (1) 當i=1時, 若δ1=22i+1,δ1<δ2≤2·(24l-2-1) (2) 當2≤i≤l時, 若δ1=22i-1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=2·22i-2-1,δ1<δ2≤24l-2i+2-1 或δ1=22i-1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1,δ1<δ2≤2·(24l-2i-1) 根據CSS構造法和定理4的結論,可構造出當m=2l時另一類碼長為n=22m-1(l≥2)非對稱量子碼的參數,見下列定理5。 定理5 設n=22m-1,m=2l(l≥2)。 (1) 若i=1,當δ1=22i+1,δ1<δ2≤2·(24l-2-1) 或δ1=22i-1-1,δ1<δ2≤24l-1-1時,存在參數為[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非對稱量子碼; (2) 若2≤i≤l,當δ1=22i-1-2,δ1<δ2≤3·24l-2i+1-1 或δ1=2·22i-2-1,δ1<δ2≤24l-2i+2-1 或δ1=22i-1+1,δ1<δ2≤24l-2i+1-1 或δ1=22i+1,δ1<δ2≤2·(24l-2i-1) 或δ1=3·22i-1+1,δ1<δ2≤24l-2i+1-3時,存在參數為[[n,n-|T(δ1)|-|T(δ2)|,dz≥δ2dx≥δ2]]4的非對稱量子碼。 說明1定理3和定理5構造出了兩類非對稱量子碼的參數,然而需要說明的是,如果對于任何一個δ,將碼的維數用公式形式表示出來是一件非常困難的事情,因此定理中用|T(δ)|表示定義集合的階,用n-|T(δ)|表示碼的維數。但是,當給定碼長n以及dz、dx時,可以精確計算出非對稱量子碼的維數,在下節(jié)中將舉例說明。 本節(jié)以m=3,4,5,6為例,將所得到的一部分碼的參數與已有文獻中的結果進行比較。下列表格中,記本文構造出的非對稱量子碼的參數為[[n,k,dz/dx]]4,文獻[8,13]中非對稱量子碼的參數記為[[n,k′,dz′/dx′]]4。 表1 dz的最大下界與δmax的比較 表1給出了m分別為3,4,5,6時,我們構造出的非對稱量子碼的z-距離的最大下界和相應的δmax的比較,可以看出我們的z-距離遠大于δmax。 表2 新的非對稱量子碼參數 表2給出m分別為3、4、5、6時,構造的新非對稱量子碼參數。需要說明當碼長n=1 023時,表中給出非對稱量子碼參數[[1 023,543,dz≥125/dx≥5]]4,實際上,當dx≥5時,dz可以達到510,但是為了便于計算,我們僅列出dz≥125的情形。 表3 非對稱量子碼參數的比較 表3給出了當m=3,4,5,6時我們構造出的非對稱量子碼的參數和已有文獻[8,13]中相關結論的比較。當碼長為n=255,dz≥6/dx≥5時,我們構造出的碼的維數為227,而文獻[13]中給出的維數為225;我們構造出的參數為[[63,33,dz≥10/dx≥5]]4的非對稱量子碼,盡管維數和文獻[8]中的相同,但是x-距離為5,而文獻中的x-距離為4。 本文利用q2-元域上碼長為n=22m-1的本原狹義BCH碼構造兩類非對稱量子[[n,k,dz/dx]]4碼的參數。首先,利用分圓陪集刻劃2個嵌套的BCH碼滿足Hermite對偶包含的條件;其次,在m=2l+1(l≥1)和m=2l(l≥2)2種情況下,根據改進了的CSS構造法和滿足Hermite對偶包含條件的2個BCH碼構造出非對稱量子碼[[n,k,dz/dx]]4的參數;最后,將所構造出的一部分結果和已有文獻中的結論進行比較,通過對參數的分析可以看出,我們得到的z-距離遠大于δmax,除了得到一些新的碼之外,還有一些碼的參數優(yōu)于已有文獻中的結論,從而提高碼的糾錯能力。 [1] Shor P W. Scheme for Reducing Decoherence in Quantum Computer Memory[J]. Phys Rev A, 1995, 52: 2493-2496 [2] Steane A M. Error-Orrecting Codes in Quantum Theory[J]. Phys Rev Lett, 1996, 77: 793-797 [3] Aly S A. Asymmetric Quantum BCH Codes[C]∥IEEE International Conference on Computer Engineering and Systems, 2008: 157-162 [4] Calderbank A R, Rains E M, Shor P W, Sloane N J A. Quantum Error-Correction via Codes over GF(4)[J]. IEEE Trans on Information Theory, 1998, 44: 1369-1387 [5] Ioffe L, Mezard M M. Asymmetric Quantum Error-Correcting Codes[J]. Phys Rev A, 2007, 75: 032345 [6] Aly S A, Ashikhmin A. Nonbinary Quantum Cyclic and Subsystem Codes over Asymmetrically-Decohered Quantum Channels[C]∥2010 IEEE Information Theory Werkshop on, 2010: 6-8 [7] Aly S A. Quantum Error Control Codes[D]. Department of Computer Science, Texas A & M University, 2008 [8] Aly S A. Asymmetric Quantum BCH Codes[C]∥International Conference on Computer Engineering and Systems, 2008: 157-162 [9] Sarvepalli P K, Klappenecker A, Rotteler M. Asymmetric Quantum Codes: Constructions, Bounds and Performance[J]. Proc R Soc A, 2009, 465: 1645-1672 [10] Wang L, Feng K, Ling S, Xing C. Asymmetric Quantum Codes: Characterization and Constructions[J]. IEEE Trans on Information Theory, 2010, 56: 2938-2945 [11] Ezerman M F, Ling S, Sole P. Additive Asymmetric Quantum Codes[J]. IEEE Trans on Information Theory, 2011, 57: 5536-5550 [12] Ezerman M F, Ling S, Pasechnik D V. CSS-Like Constructions of Asymmetric Quantum Codes[J]. IEEE Trans on Inf Theory, 2013, 59: 6732-6754 [13] La Guardia G G. On the Construction of Asymmetric Quantum Codes[J]. Int J Theory Phys, 2014, 53: 2312-2322 [14] La Guardia G G. Asymmetric Quantum Codes: New Codes from Old[J]. Quantum Information Process, 2013, 12: 2771-2797 [15] La Guardia G G. New Families of Asymmetric Quantum BCH Codes[J]. Quantum Inform Computation, 2011, 11: 239-252 [16] Chen J Z, Li J P, Huang Y Y. Some Families of Asymmetric Quantum Codes and Quantum Convolutional Codes from Constacyclic Codes[J]. Linear Algebra and its Applications, 2015, 475: 186-199 [17] Huffman W C, Pless V. Fundamentals of Error-Correcting Codes[M]. Cambridge, U K: Cambridge University Press, 2003 [18] Macwilliams F J , Sloane N J A. The Theory of Error-Correcting Codes[M]. Amsterdam, the Netherlands: North-Holland, 1977 [19] Li R H, Xu G, Guo L B. On Two Promblems of Asymmetric Quantum Codes[J]. International Journal of Modern Physics Letter B, 2014, 28: 1450017-1450031 [20] Ma Y N, Feng X Y, Lv L D. Dual Containing BCH Codes and New Asymmetric Quantum Codes[C]∥5th International Conference on Instrumentation and Measurement, Computer, Communication, and Control, 2015: 1575-1578 [21] Ma Y N, Feng X Y, Xu G. New Asymmetric Quantum Codes overFq[J]. Quantum Information Process, 2016, 15: 2759-2769 Two Families of Dual Containing BCH Codes Ma Yuena1,2, Feng Xiaoyi1, Su Zhizhong3, Liu Yang2,3 1.School of Electronics and Information, Northwestern Polytechnical University, Xi′an 710072, China 2.School of Science, Air Force Engineering University, Xi′an 710051, China 3.The First Aeronautical College of Air Force, Xinyang 464000, China In this paper, we discuss the problem on the construction of asymmetric quantum codes from primitive narrow sense BCH codes. Take advantage ofq2-ary Hermite dual containing BCH code, we construct two families of new asymmetric quantum codes with much largerz-distance. Furthermore, the parameters of our asymmetric quantum codes presented here have better than the ones avaliable in the literature. asymmetric quantum code; BCH code; Hermite dual containing; CSS construction 2016-04-12 國家自然科學基金(11471011)與陜西省自然科學基金(2015JM1023)資助 馬月娜(1977—),女,西北工業(yè)大學博士研究生,主要從事編碼與密碼、圖像處理及模式識別研究。 O157.4 A 1000-2758(2016)05-0874-05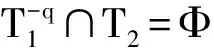

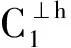
2 兩類非對稱量子糾錯碼的構造


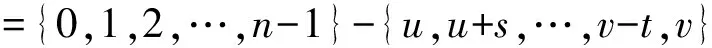
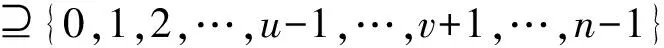
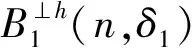
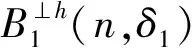
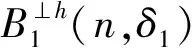
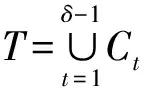
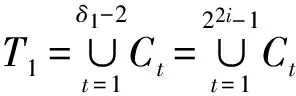
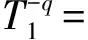
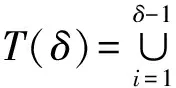
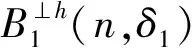
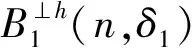
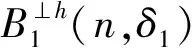
3 參數分析

4 結 論

