基于曲梁模型的大展弦比大柔性機(jī)翼顫振分析

段靜波, 周洲, 江濤

(1.西北工業(yè)大學(xué) 航空學(xué)院, 陜西 西安 710072; 2.軍械工程學(xué)院 無人機(jī)工程系, 河北 石家莊 050003)

?

基于曲梁模型的大展弦比大柔性機(jī)翼顫振分析

段靜波1,2, 周洲1, 江濤2

(1.西北工業(yè)大學(xué) 航空學(xué)院, 陜西 西安 710072; 2.軍械工程學(xué)院 無人機(jī)工程系, 河北 石家莊 050003)

提出一種大展弦比大柔性機(jī)翼顫振分析的方法。該方法首先引入準(zhǔn)模態(tài)假設(shè)，將氣動載荷作用下發(fā)生大靜變形的大展弦比大柔性機(jī)翼視為一根變曲率曲梁，并將其離散為一系列常曲率曲梁單元，利用機(jī)翼靜變形結(jié)果，通過多項(xiàng)式插值獲得各曲梁單元的平均曲率。其次，在曲梁單元內(nèi)，利用曲梁振動微分方程和Therdorson非定常氣動力模型建立曲梁單元的顫振微分方程。然后，運(yùn)用傳遞函數(shù)法，將曲梁單元的顫振微分方程轉(zhuǎn)換為狀態(tài)空間形式，并依照有限元組集的思想形成機(jī)翼整體平衡方程。最后，通過求解特征值問題獲得機(jī)翼的顫振速度和顫振頻率。通過與已有文獻(xiàn)結(jié)果的對比，驗(yàn)證了新方法的正確性和有效性。

大展弦比；大柔性機(jī)翼；曲梁；非定常氣動力；顫振

大展弦比大柔性機(jī)翼在氣動載荷作用下通常經(jīng)歷較大的結(jié)構(gòu)變形。準(zhǔn)確把握這類大變形機(jī)翼的氣動彈性特性是目前研究的熱點(diǎn)之一。國內(nèi)外學(xué)者開展了較多卓有成效的研究工作。Smith Patil等[1-2]較早地開展了基于CFD方法的大展弦比機(jī)翼氣動彈性特性研究。機(jī)翼由Hodges-Dowell梁來模擬，氣動力計算則以Euler方程為基礎(chǔ)。Garcia[3]應(yīng)用精確梁理論的有限元方法，并耦合N-S方程的氣動力，計算了大展弦比機(jī)翼的跨音速靜氣動彈性特性。Palacois、Beran等[4-5]基于流固耦合方法，分別研究了超大展弦比機(jī)翼和翼身融合體飛機(jī)的靜氣動彈性問題。國內(nèi)方面，謝長川等[6-7]應(yīng)用“準(zhǔn)模態(tài)”假設(shè)，分析結(jié)構(gòu)幾何非線性對大展弦比機(jī)翼振動的影響，即認(rèn)為結(jié)構(gòu)是在大的靜變形平衡位置附近作微幅振動，從而可沿用線性系統(tǒng)振動理論進(jìn)行機(jī)翼振動描述，通過算例驗(yàn)證了方法的有效性。周洲等[8-9]基于CR有限元理論，推導(dǎo)了大柔性機(jī)翼的切線剛度矩陣和質(zhì)量矩陣，建立了考慮幾何非線性效應(yīng)的大柔性無人機(jī)結(jié)構(gòu)動力學(xué)模型，并引入準(zhǔn)模態(tài)小擾動振動假設(shè)，對動力學(xué)模型進(jìn)行線性化，并采用建立在局部氣流坐標(biāo)系下的Therdorson片條非定常氣動力，通過p-k法對無人機(jī)的非線性顫振速度和頻率進(jìn)行了求解。楊智春和黨會學(xué)等[10]耦合Euler方程求解器和非線性結(jié)構(gòu)求解器，計算了大展弦比機(jī)翼的靜變形，并在靜變形的基礎(chǔ)上，提取結(jié)構(gòu)的剩余剛度進(jìn)行了非線性顫振特性分析。向錦武等[11]研究了側(cè)向隨動力作用下大展弦柔性機(jī)翼氣動彈性穩(wěn)定性等問題。

本文在前人研究的基礎(chǔ)上，發(fā)展了一種大展弦比大柔性機(jī)翼顫振分析的方法，通過與已有文獻(xiàn)結(jié)果的對比，驗(yàn)證了本文方法的正確性和有效性。

1 機(jī)翼顫振微分方程建立

1.1 機(jī)翼大靜變形曲線方程擬合

大展弦比大柔性機(jī)翼靜變形后可視為一根曲梁。梁橫截面的剛心軸線形成一條曲線，在直角坐標(biāo)系XOY下如圖1所示。

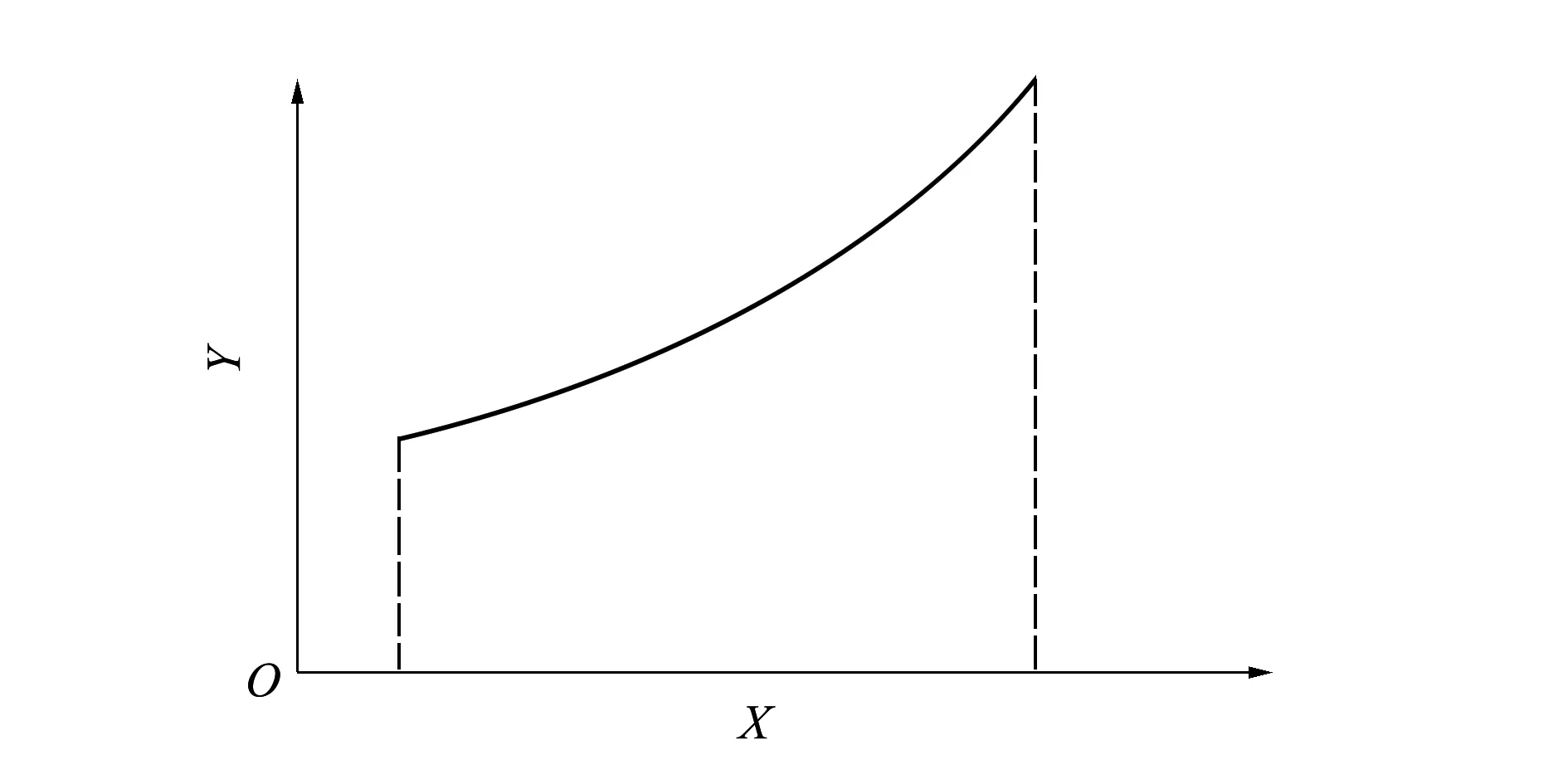
圖1 變曲率曲梁的示意圖

將曲梁劃分若干段，每段為一個曲梁單元。在直角坐標(biāo)系下，每個曲梁單元的起點(diǎn)和終點(diǎn)的坐標(biāo)以及斜率均可根據(jù)機(jī)翼靜變形給出，從而通過多項(xiàng)式插值可將曲梁單元的曲線方程表示出來，為[12]：

(1)

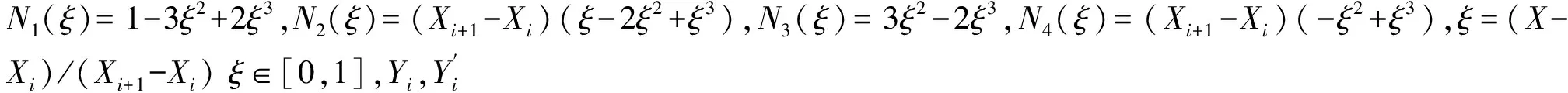
由曲線的曲率公式可知曲梁單元內(nèi)任一點(diǎn)的曲率半徑為

(2)

每個曲梁單元內(nèi)的曲率可近似為常數(shù),可取單元兩端處的曲率半徑平均值作為該單元的平均曲率半徑。

1.2 曲梁單元振動微分方程

在曲梁單元內(nèi),曲梁的曲率可視為常數(shù)R,其自然坐標(biāo)系如圖2所示,x軸表示切向,y軸表示徑向,z軸表示豎向。根據(jù)文獻(xiàn)[13],考慮曲梁質(zhì)心軸與彈性軸不重合的情形,可獲得曲梁六自由度振動方程為

(3)

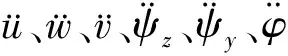
1.3 非定常氣動力模型

在忽略機(jī)翼重力影響條件下,機(jī)翼顫振時的外力為氣動力產(chǎn)生的分布升力以及分布扭矩。本文采用片條理論進(jìn)行非定常氣動力計算。氣動力片條在曲梁形狀基礎(chǔ)位置上定義,且位于曲梁單元中點(diǎn)處。根據(jù)Theodorson理論,單位展長的非定常升力與相應(yīng)的俯仰力矩按下式計算[14]

(4)

式中,k=ωb/V為折合頻率,是一個無量綱參數(shù),C(k)為Theodorsen函數(shù),由于k是ω和V的函數(shù),為了后續(xù)求解方便,將C(k)寫為C(ω,V),其他符號含義同文獻(xiàn)[8]。

1.4 機(jī)翼單元顫振微分方程

將(4)式代入(3)式后就可得機(jī)翼單元顫振時的微分方程

(5)

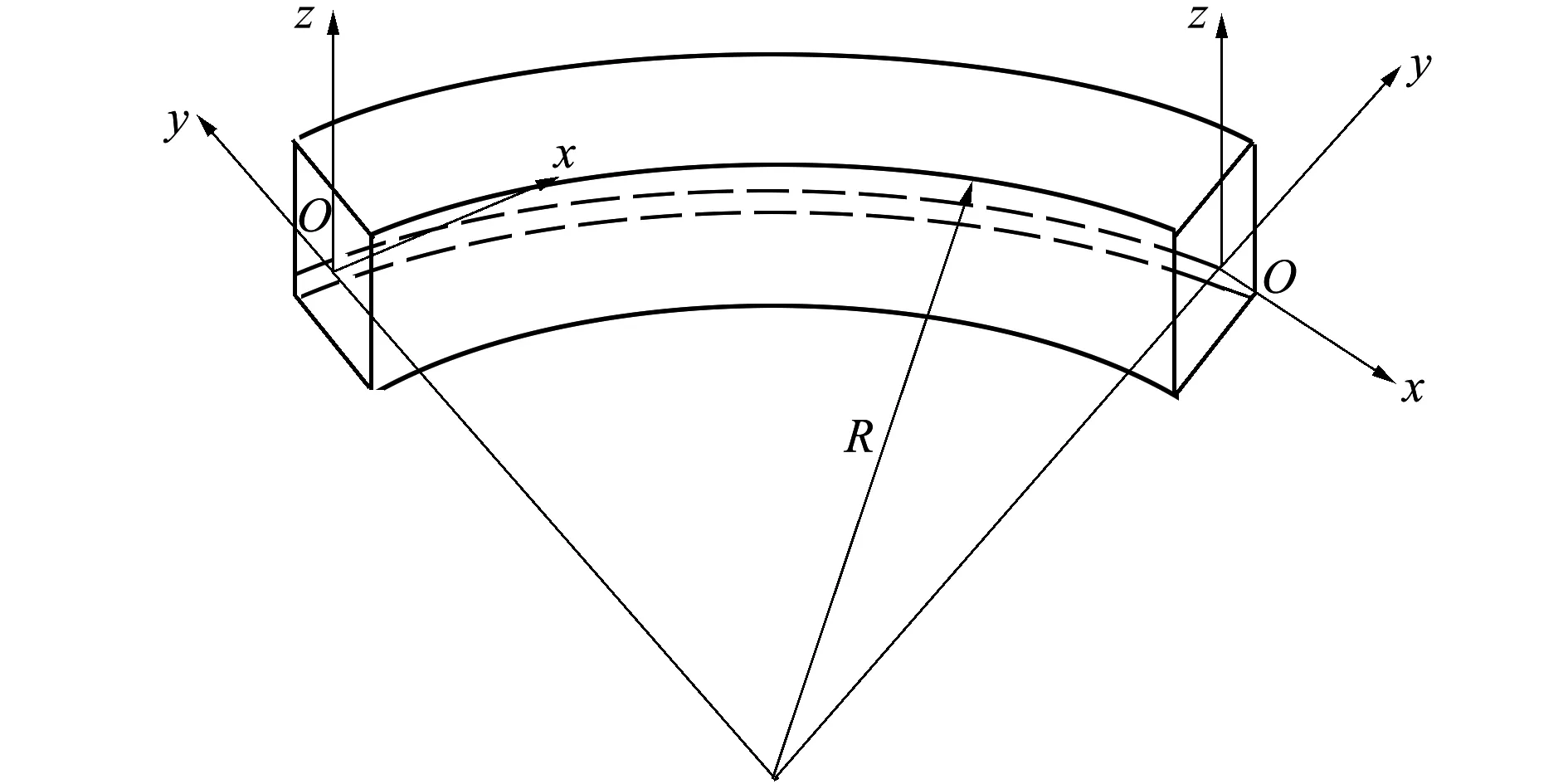
圖2 曲梁單元自然坐標(biāo)系

2 機(jī)翼顫振的傳遞函數(shù)求解

2.1 機(jī)翼單元的傳遞函數(shù)

對機(jī)翼單元顫振微分方程(6)式進(jìn)行Fourier變換,并整理可得

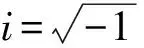
定義單元狀態(tài)向量

(7)

將(6)式改寫為狀態(tài)空間形式的方程

(8)

式中,ge(x,ω)=0,轉(zhuǎn)移矩陣Fe(ω,V)為12×12的方陣,其非零元素為

邊界條件為

(9)

式中,l為曲梁單元長度,Mb、Nb分別為單元邊界條件選擇矩陣,為12×12的方陣,其非零元素為

Nb(10,8)=1,Nb(11,10)=1,Nb(12,12)=1

γe(ω)為由位移或力組成的列向量,其表達(dá)式為

方程(8)式的傳遞函數(shù)解為

(10)

式中

(11)

2.2 系統(tǒng)的合成與求解

由于大變形后的機(jī)翼劃分為若干常曲率曲梁單元來描述整個機(jī)翼,其求解方程可借鑒有限元方法的思想進(jìn)行組集。具體如下:

曲梁單元截面上的內(nèi)力為

(12)

式中,My、Mz分別為曲梁單元繞x、y、z軸彎矩,Tx分別為曲梁單元繞x軸的扭矩,Nx為沿x軸的軸力,Qy和Qz分別為沿y、z軸的剪力。

將曲梁單元內(nèi)力寫成矩陣形式

(13)

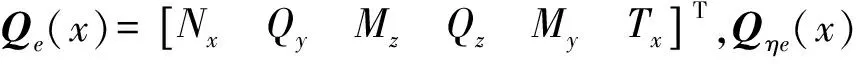
將(10)式代入(13)式后,取x=0、l,可得到曲梁單元兩端點(diǎn)處的內(nèi)力

(14)

式中

上式與有限元法中單元節(jié)點(diǎn)力表達(dá)式十分相似,fe可視為單元節(jié)點(diǎn)內(nèi)力,Ke(ω,V)可視為單元剛度矩陣,γe(ω)可視為單元節(jié)點(diǎn)位移向量。

按照有限元組集方法對各節(jié)點(diǎn)統(tǒng)一編號,并進(jìn)行組集拼接,可得到機(jī)翼整體平衡方程為

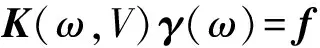
(15)

式中,K(ω,V)可視為整體剛度矩陣,γ(ω)可視為整體節(jié)點(diǎn)位移向量,f為各單元節(jié)點(diǎn)內(nèi)力拼裝成的向量。由于本文中將機(jī)翼的氣動力與機(jī)翼作為一個完整的系統(tǒng)來考慮,除此之外,機(jī)翼沒有受到其它外力作用,因而根據(jù)單元節(jié)點(diǎn)內(nèi)力與外載荷平衡,可得出

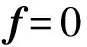
(16)

根據(jù)機(jī)翼約束條件,按照有限元方法對整體剛度矩陣K(ω,V)進(jìn)行邊界條件處理[15-16]。

當(dāng)機(jī)翼顫振時,γ(ω)應(yīng)有非零解,此時須滿足條件

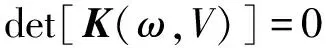
(17)

由于K(ω,V)為復(fù)矩陣,其行列式值等于零的必要條件為矩陣行列式值的實(shí)部與虛部均為零,即

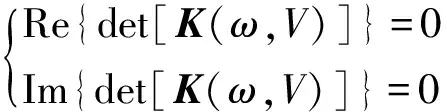
(18)

(18)式2個方程包含2個未知變量V和ω,因而求解(18)式可得到V和ω的解。其中,V即為機(jī)翼顫振速度,ω即為機(jī)翼顫振頻率。通常滿足(18)式條件的解可能有多個,其中V最小的一組解即為機(jī)翼的顫振特性。

3 結(jié)果與分析

3.1 方法驗(yàn)證

為了驗(yàn)證本文方法的正確性,按照文獻(xiàn)[8]算例計算大展弦比柔性機(jī)翼的氣動彈性穩(wěn)定性。大柔性大展弦比機(jī)翼的幾何參數(shù)、剛度參數(shù)和質(zhì)量參數(shù)均與文獻(xiàn)[8]一致,見表1所示。

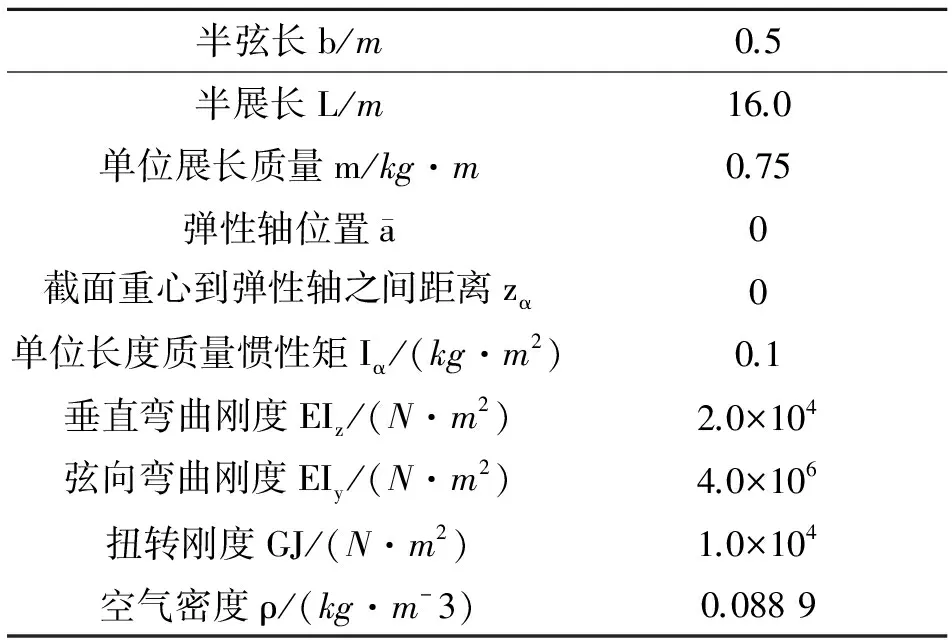
表1 機(jī)翼模型參數(shù)

通過表1中機(jī)翼模型參數(shù),假設(shè)機(jī)翼為平板翼型可反推出本文方法所需要的參數(shù)。

文獻(xiàn)[8]給出了機(jī)翼翼尖作用集中力下的機(jī)翼撓度曲線。本文取翼尖位移分別為機(jī)翼半展長的3.125%、6.250%、12.50%的變形情形,分別記為變形一、變形二、變形三。將變形后的機(jī)翼視為曲梁,分別擬合出機(jī)翼變形后的曲線方程,沿機(jī)翼展向劃分10個單元后,按(2)式計算每個單元的平均曲率半徑,然后利用本文方法計算機(jī)翼顫振特性。

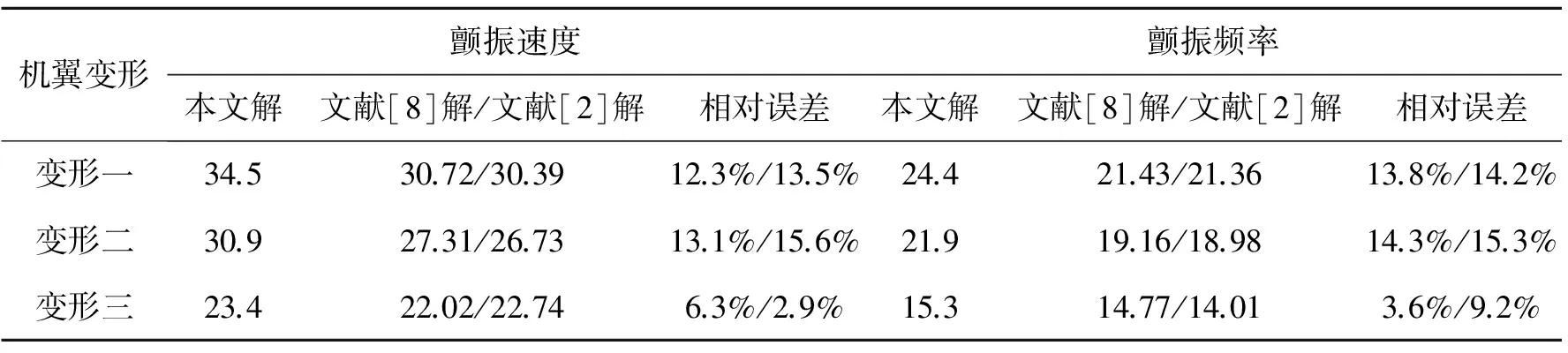
表2 機(jī)翼顫振結(jié)果

圖3至圖5給出了大展弦比大柔性機(jī)翼在不同程度靜變形下求解機(jī)翼的顫振速度和顫振頻率的過程。

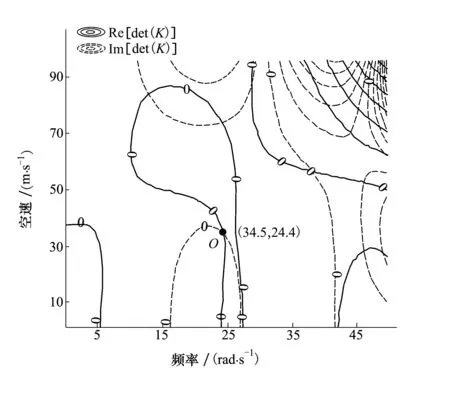
圖3 Re[det(K)]和Im[det(K)]的等值線圖(變形一)

圖3為機(jī)翼變形一時,(18)式中Re[det(K)]和Im[det(K)]的等值線圖。圖中Re[det(K)]和Im[det(K)]的零等值線交點(diǎn)即為滿足(18)式的解。從圖中可以看到,同時滿足(18)式且V最小的一組解(V,ω)=(34.5,24.4),即為圖3中O點(diǎn)。這表明,機(jī)翼變形一時,機(jī)翼的顫振速度為34.5 m/s,機(jī)翼的顫振頻率為24.4 rad/s。

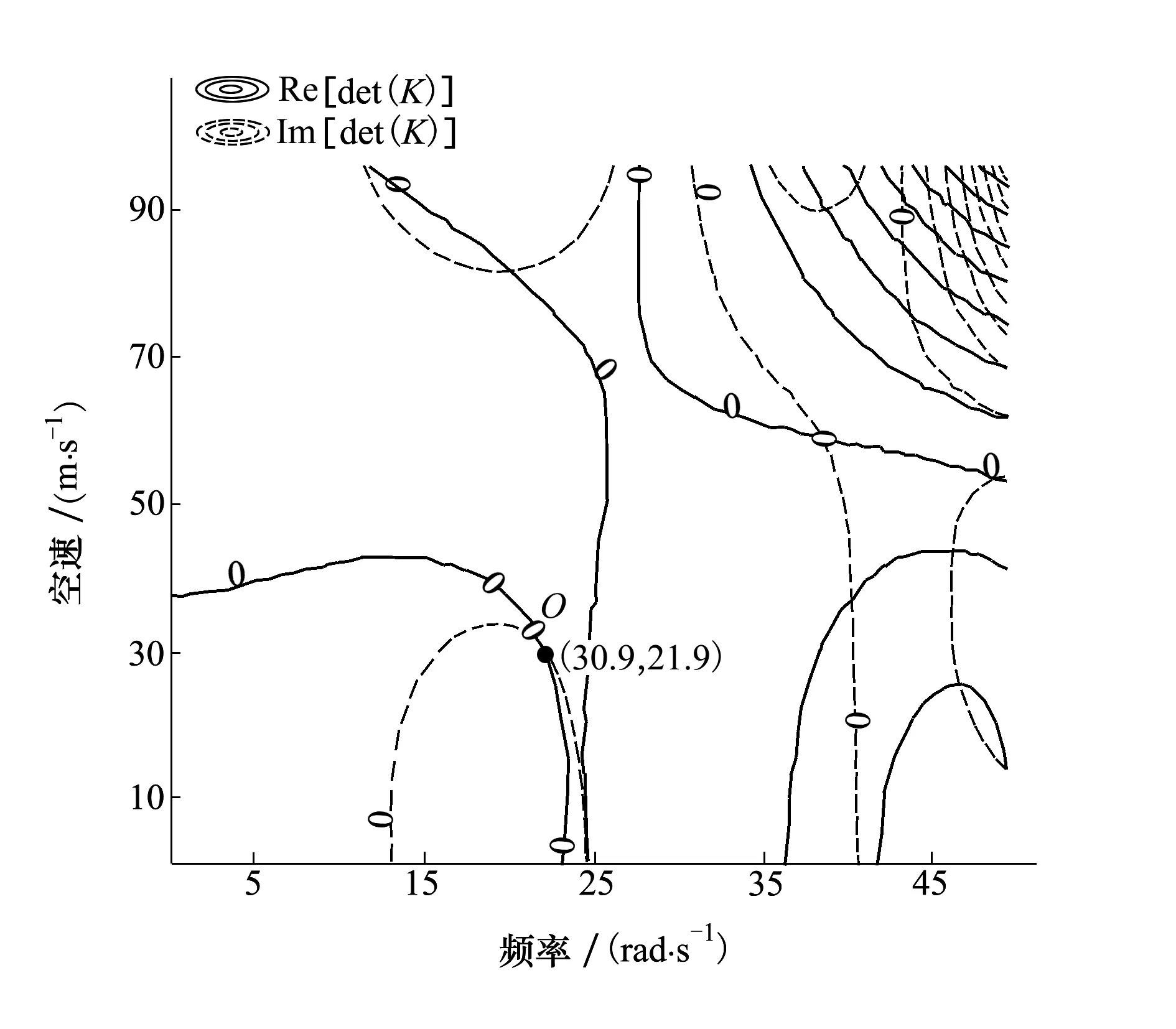
圖4 Re[det(K)]和Im[det(K)]的等值線圖(變形二)

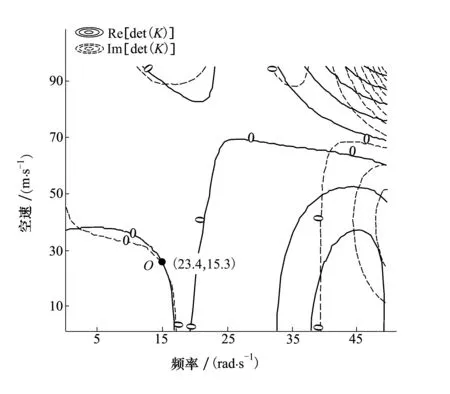
圖5 Re[det(K)]和Im[det(K)]的等值線圖(變形三)

同樣,圖4和圖5分別為機(jī)翼變形二、變形三時的Re[det(K)]和Im[det(K)]等值線圖,由圖中O點(diǎn)可以得到機(jī)翼的顫振特性。

為了便于比較，將計算得到的機(jī)翼3種變形下的顫振速度和顫振頻率列入表2中，并與已有文獻(xiàn)結(jié)果進(jìn)行對比。從表中可以看出，本文方法與文獻(xiàn)的結(jié)果基本吻合。兩者存在一定差異的主要原因在于：文獻(xiàn)中進(jìn)行氣彈分析時，在結(jié)構(gòu)方面進(jìn)行了動力學(xué)降階，利用了機(jī)翼若干低階模態(tài)，模態(tài)的選用可能會影響結(jié)果的精度；在氣動力模型方面，采用的模型考慮了機(jī)翼的三維效應(yīng)。本文方法在結(jié)構(gòu)方面直接采用微分方程，避免了模態(tài)降階，在氣動力模型方面采用了片條理論，沒有考慮機(jī)翼的三維效應(yīng)。

此外，從表2中還可以看出，隨著機(jī)翼變形量增大，本文結(jié)果與參考文獻(xiàn)結(jié)果的相對誤差逐漸減小。這其中主要的原因是，用曲梁模型模擬機(jī)翼時，當(dāng)機(jī)翼變形較小時，曲梁單元的曲率半徑誤差較大，隨著機(jī)翼變形增大，曲梁單元的曲率半徑誤差逐漸減小。

3.2 機(jī)翼顫振特性影響分析

采用本文方法，將劃分單元數(shù)目、彎曲剛度比、扭轉(zhuǎn)剛度、質(zhì)心弦向位置等作為變量，以上節(jié)中的3種變形情形作為基準(zhǔn)，研究上述因素對大變形機(jī)翼顫振特性的影響。

表3給出了單元數(shù)目對機(jī)翼顫振速度和顫振頻率收斂性的影響。從表中可以看出，當(dāng)采用10個單元后，結(jié)果已收斂。這表明本文方法使用較少單元即可較快收斂，因而非常適合總體設(shè)計階段的機(jī)翼顫振特性快速分析要求。

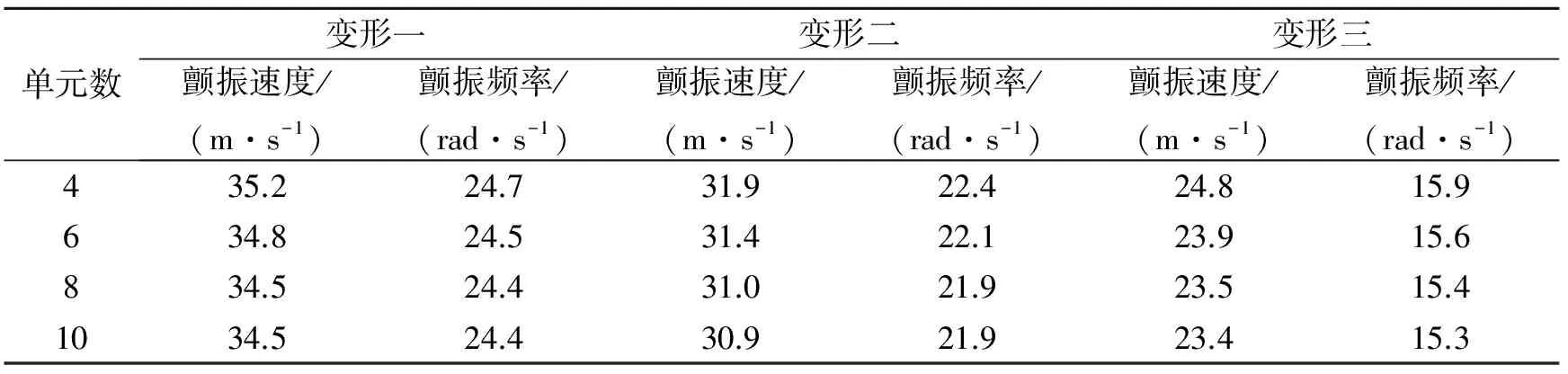
表3 單元數(shù)目對機(jī)翼顫振結(jié)果的影響

圖6給出了3種不同變形情形下扭轉(zhuǎn)剛度變化對機(jī)翼顫振速度的影響。從圖中可以看到，隨著扭轉(zhuǎn)剛度增大，不同變形條件下機(jī)翼顫振速度都有了提高。但是，機(jī)翼變形程度不同時，機(jī)翼顫振速度增加是有差別的。在變形一情形下，機(jī)翼變形相對較小，機(jī)翼顫振速度增幅相對較大；變形三情形下，機(jī)翼相對變形較大，機(jī)翼顫振速度增幅相對降低。這表明，隨著機(jī)翼變形越來越大，通過提高扭轉(zhuǎn)剛度改善機(jī)翼顫振特性的效果會有所降低。主要原因是：在機(jī)翼大變形下，靠近翼尖的結(jié)構(gòu)大變形會顯著改變機(jī)翼的扭轉(zhuǎn)振動特性，進(jìn)而影響扭轉(zhuǎn)剛度增加改善機(jī)翼顫振特性的效果。

圖7給出了3種不同變形情形下機(jī)翼弦向彎曲剛度與垂直彎曲剛度比對機(jī)翼顫振速度的影響。從圖中可以看到，在弦向彎曲剛度與垂直彎曲剛度比較小時，3種變形狀態(tài)下的機(jī)翼顫振速度對彎曲剛度比均比較敏感度，而且機(jī)翼顫振速度在機(jī)翼變形相對小時更敏感；當(dāng)彎曲剛度比較大時，機(jī)翼顫振速度對其敏感度逐漸降低，此時弦向彎曲剛度具有較大的設(shè)計空間。

質(zhì)心軸在弦向的位置是非常重要的氣動彈性設(shè)計量，在上節(jié)研究中，剖面質(zhì)心與剛心均位于弦長中點(diǎn)處，這里仍然假定兩者重合，以其在弦向的位置作為變量，研究質(zhì)心弦向位置對大變形機(jī)翼顫振特性的影響。圖8給出了3種不同變形情形下質(zhì)心弦向位置對機(jī)翼顫振速度的影響。從圖中可以看到，在機(jī)翼弦向中點(diǎn)前后10%半展長范圍內(nèi)，隨著質(zhì)心沿弦向從前向后移動，機(jī)翼顫振速度逐漸降低。這一結(jié)論與剛性機(jī)翼顫振特性相似。但是，隨著機(jī)翼變形越來越大，機(jī)翼顫振速度降低幅度加快。圖中可以看，變形三情形下機(jī)翼顫振速度下降快于變形一、變形二。

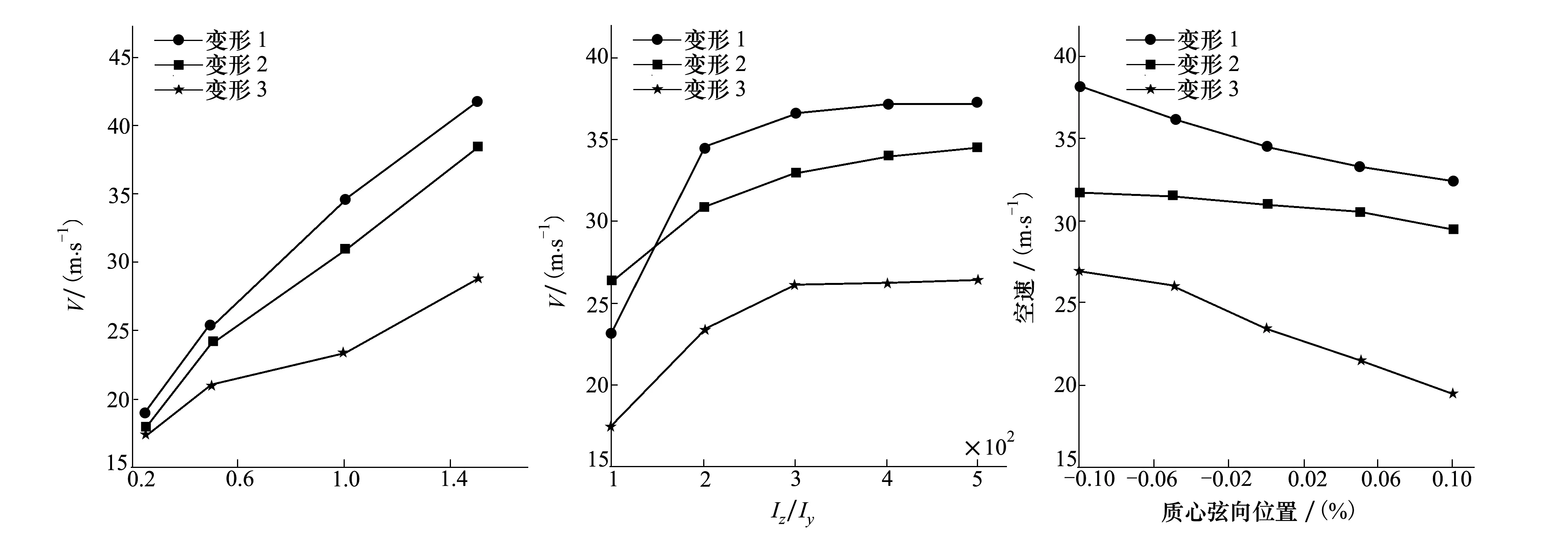
圖6 扭轉(zhuǎn)剛度對機(jī)翼顫振速度的影響 圖7 彎曲剛度比對機(jī)翼顫振速度的影響 圖8 質(zhì)心弦向位置對機(jī)翼顫振速度的影響

4 結(jié) 論

本文提出了一種大展弦比大柔性機(jī)翼顫振的分析方法。該方法將大變形后機(jī)翼視為一根變曲率曲梁，從而不僅可以通過曲梁形狀考慮大展弦比大柔性機(jī)翼變形中的幾何非線性因素，而且仍然可以運(yùn)用曲梁線性振動理論來近似描述大變形機(jī)翼的動力學(xué)特性。在求解機(jī)翼的顫振特性時，采用傳遞函數(shù)法進(jìn)行求解，方法計算規(guī)模小、收斂快，非常適合工程總體設(shè)計階段的快速分析要求，而且該方法還可進(jìn)一步推廣應(yīng)用于機(jī)翼氣動彈性響應(yīng)計算。

[1] Smith M J, Patil M J, Hodges D H. CFD-Based Analysis of Nonlinear Aeroelastic Behavior of High-Aspectratio Wings[R]. AIAA-2001-1582

[2] Patil M J, Hodges D H. Limit-Cycle Oscillations in High-Aspect-Ratio Wings[J]. Journal of Fluid and Structures, 2001,15:07-132

[3] Garcia J A. Numerical Investigation of Nonlinear Aeroelastic Effects on Flexible High-Aspect Ratio Wings[J]. Journal of Aircraft, 2005, 42(4):1025-1036

[4] Palacios R, Cesni C S. Static Nonlinear Aeroelasticity of Flexible Slender Wings in Compressible Flow[R]. AIAA-2005-1945

[5] Beran P S, Hur J Y, Snder R D. Static Nonlinear Aeroelastic Analysis of a Blended wing Body[R]. AIAA-2005-1944

[6] 謝長川,吳志剛,楊超. 大展弦比柔性機(jī)翼的氣動彈性分析[J]. 北京航空航天大學(xué)學(xué)報, 2003, 29(12): 1087-1091

Xie Changchuan, Wu Zhigang, Yang Chao. Aeroelastic Analysis of Flexible Large Aspect Ratio Wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(12):1087-1091 (in Chinese)

[7] Xie Changchuan, Leng Jiazhen, Yang Chao. Geometrical Nonlinear Aeroelastic Stability Analysis of a Composite High-Aspect-Ratio Wing[C]∥International Conference on Engineering Dynamics, 2007

[8] 王偉,周洲,祝小平,王睿. 幾何大變形太陽能無人機(jī)非線性氣動彈性穩(wěn)定性研究[J]. 西北工業(yè)大學(xué)學(xué)報, 2015,33(1): 1-8

Wang Wei, Zhou Zhou, Zhu Xiaoping, Wang Rui. Exploring Aeroelastic Stability of Very Flexible Solar Powered UAV with Geometrically Large Deformation[J]. Journal of Northwestern Polytechnical University, 2015, 33(1): 1-8 (in Chinese)

[9] 王偉,周洲,祝小平,王睿. 考慮幾何非線性效應(yīng)的大柔性太陽能無人機(jī)靜氣動彈性分析[J]. 西北工業(yè)大學(xué)學(xué)報, 2014,32(4): 499-505

Wang Wei, Zhou Zhou, Zhu Xiaoping, Wang Rui. Static Aeroelastic Characteristics Analysis of a Very Flexible Solar Powered Uav With Geometrical Nonlinear Effect Considered[J]. Journal of Northwestern Polytechnical University, 2014,32(4): 499-504 (in Chinese)

[10] 楊智春,黨會學(xué),李毅. 大展弦比機(jī)翼非線性氣動彈性特性的數(shù)值模擬研究[C]∥第十一屆全國空氣彈性學(xué)術(shù)交流會, 2009

Yang Zhichun, Dang Huixue, Li Yi. Numerical Simulation of Nonlinear Aeroelastic Characteristics for a High-Aspect-Ratio Wing[C]∥11th Conference on Aeroelasticity, 2009 (in Chinese)

[11] 張健, 向錦武. 側(cè)向隨動力作用下大展弦柔性機(jī)翼的穩(wěn)定性[J]. 航空學(xué)報，2010, 31(11): 2115-2123

Zhang Jian, Xiang Jingwu. Stability of High-Aspect-Ratio Flexible Wings Loaded By a Lateral Follower Force[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11):2115-2124 (in Chinese)

[12] 蔣純志. 分布傳遞函數(shù)方法在梁桿結(jié)構(gòu)分析中的應(yīng)用[D]. 長沙：國防科技大學(xué), 2006

Jiang Chunzhi. The Application of Distributed Transfer Function Method to Girders and Beams Analysis[D]. Changsha, National University of Defense Technology, 2006 (in Chinese)

[13] 趙雪健. 平面曲梁自由振動的動力剛度法研究[D]. 北京：清華大學(xué)，2010

Zhao Xuejian. Research on Dynamic Stiffness Method for Free Vibration of Planar Curve Beams[D]. Beijing, Tingshua University, 2013 (in Chinese)

[14] 趙永輝. 氣動彈性力學(xué)與控制[M]. 北京: 科學(xué)出版社, 2006

Zhao Yonghun. Aeroelastic Mechanics and Control[M]. Beijing, Science Press, 2006 (in Chinese)

[15] 李海陽. 數(shù)學(xué)物理問題的數(shù)值分布傳遞函數(shù)方法[D]. 長沙:國防科技大學(xué),1999

Li Haiyang. Numerical Transfer Function Method for Mathematic and Physical Problems[D]. Changsha, National University of Defense Technology, 1999 (in Chinese)

[16] 雷勇軍. 結(jié)構(gòu)分析的分布參數(shù)傳遞函數(shù)方法[D]. 長沙:國防科技大學(xué),1998

Lei Yongjun. Distributed Transfer Function Method for Structural Analysis[D]. Changsha, National University of Defense Technology, 1998 (in Chinese)

A Method for Flutter of the Very Flexible Wing with High-Aspect-Ratio Based on Curve Beam Model

Duan Jingbo1,2, Zhou Zhou1, Jiang Tao2

1.School of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.Department of UAV Engineering, Ordnance Engineering College, Shijiazhuang 050003, China

A method for flutter of the very flexible wing with a high-aspect-ratio is developed. Firstly, the very flexible wing subjected to aeroelastic load will undergo a large deformation. So the deformed wing can be regarded as a curve beam and divided into a couple of curve beam elements. The mean curvature of every beam element is obtained by mean of polynomial interpolation method. For each element, the flutter differential equations is established by combining the differential equations of the constant curvature beam vibration and the Therdorson' unsteady aerodynamics model. Then, using the distributed transfer function method and the finite element method, the equilibrium equations of the whole wing are obtained. Finally, the wing flutter was carried out by solving a eigenvalue problem. The results are good agreement to the literature solutions and indicate that the present method is accurate and efficient.

high-aspect-ratio; very flexible wing; curve beams; unsteady aerodynamics; flutter

2016-03-02

中國博士后基金(2014M560803)資助

段靜波(1982―)，西北工業(yè)大學(xué)博士后，主要從事飛行器氣動彈性研究。

V215.3

A

1000-2758(2016)05-0774-09