微小衛星姿態控制系統魯棒自適應故障估計

張科, 韓治國, 楊天社, 王靖宇

(1.西北工業大學 航天學院, 陜西 西安 710072; 2.中國西安衛星測控中心, 陜西 西安 710043)

?

微小衛星姿態控制系統魯棒自適應故障估計

張科1, 韓治國1, 楊天社2, 王靖宇1

(1.西北工業大學 航天學院, 陜西 西安 710072; 2.中國西安衛星測控中心, 陜西 西安 710043)

針對具有非結構不確定項的非線性系統中存在的執行器與傳感器故障，采用一種基于描述系統的故障估計觀測器設計方法。該方法具有期望的魯棒性能指標，能夠在系統存在不確定項干擾的情況下實現對突變故障與時變故障等故障類型的精確估計。根據Lyapunov穩定性理論推導了上述方法存在的充分條件，根據線性化算法把上述充分條件轉變為準線性矩陣不等式，應用迭代優化算法求得該充分條件的可行解。最后，將該方法應用于微小衛星姿態控制系統中執行器與傳感器故障估計，仿真結果證明了該方法的有效性。

姿態控制；線性矩陣不等式；故障估計；Lyapunov函數

隨著對高性能與高可靠性要求的增加，衛星姿態控制系統變得越來越精細與復雜。這樣的復雜系統不可避免地存在各種各樣的故障，尤其是陀螺、強磁計、太陽敏感器以及動量輪等傳感器與執行器故障，這些故障將會降低系統的性能，甚至帶來災難性的后果。因此，近幾年來衛星姿態控制系統的故障估計問題越來越受到研究者的重視，成為了重要的研究方向，取得了一些富有成效的研究成果[1-4]。

在過去的二十年間，根據先進控制理論，研究了各種各樣的故障估計方法。如基于滑模觀測器方法、基于未知輸入觀測器方法、自適應觀測器方法以及描述觀測器方法等[5-9]。文獻[5]針對離散時間線性系統，提出了魯棒故障估計觀測器設計方法，能夠實現對系統狀態與執行器故障的同時估計；文獻[6]采用觀測器方法對航天器存在的執行機構失效故障和外部干擾問題進行故障檢測與重構；在文獻[7]中，將執行器故障作為增廣狀態向量構造一個增廣系統，利用線性矩陣不等式方法設計了一個增廣狀態觀測器，能夠同時獲得原系統的狀態和執行器故障的漸近估計；文獻[8]基于故障診斷濾波器設計方法實現對離散線性描述系統的執行器故障診斷；文獻[9]針對線性系統，根據已有的自適應故障診斷觀測器設計方法，提出了一種增廣故障診斷觀測器設計方法，拓展了自適應故障診斷觀測器的適用范圍。

我們注意到，上述研究成果大多是針對線性系統，而且只有文獻[8]研究了描述系統的故障診斷問題。根據上述研究成果，本文針對滿足Lipschitz條件的非線性系統，采用一種魯棒自適應觀測器設計方法，該方法能夠同時估計執行器與傳感器故障。通過把傳感器故障作為增廣狀態，建立增廣系統模型，應用魯棒自適應觀測器同時估計系統狀態、傳感器與執行器故障。最后將該方法應用于微小衛星姿態控制系統中執行器與傳感器故障估計問題，通過數值仿真證明了該方法在衛星姿態控制系統傳感器與執行器故障估計方面的有效性。

1 問題描述

根據文獻[10-11]，衛星姿態動力學方程可以由下式描述:

(1)

式中,J=diag{J1,J2,J3}為衛星的轉動慣量,ω=[ωx,ωy,ωz]T為衛星本體相對慣性坐標系的角速度在星體坐標系中的表示,u=[u1,u2,u3]T為控制力矩,非線性項為ζ=[-sinθ,sinφcosθ,cosφcosθ]T,ω0為軌道角速度,Td=[Td1,Td2,Td3]T為外部干擾力矩,歐拉角φ、θ、ψ分別為滾轉、俯仰與偏航角,斜對稱矩陣由下式描述

(2)

當姿態角較小時,動力學方程(1)可以寫成

(3)

衛星的運動學方程經過線性化可以描述為

(4)

選取狀態變量x=[φ,θ,ψ,ωx,ωy,ωz]T,則含有系統不確定項Δψ(t)以及傳感器故障fs與執行器故障fa的衛星姿態控制系統可描述為

(5)

(6)

如果把傳感器故障作為附加狀態,可以得到如下的增廣描述系統形式[11]

(7)

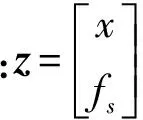
注1 在上述增廣過程中并未采用任何假設,所以系統(5)和(7)是完全等價的。

注2 微小衛星的姿態控制系統不同于較大衛星,較大衛星的柔性與模型的緩變衰減是建模時應該主要考慮的影響因素。而對于微小衛星,由于不存在柔性特性,可以把它作為剛體進行考慮。

在進行故障估計觀測器設計之前,首先給出如下合理假設。

假設1 假設系統(5)是能控能觀系統,非線性項f(x,t)滿足Lipschitz條件,即

(8)

式中:Lf是Lipschitz常數。

從形式上看,系統(7)是一個描述系統,所以本文將從描述系統出發,進行故障估計觀測器設計。

2 故障估計觀測器設計

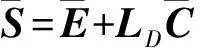
基于上述討論,對系統(7)采用如下觀測器[4]

(9)

針對上述觀測器,采用如下的自適應故障估計率[4,9]

(10)

式中:Γ∈Rm×m是對稱正定矩陣,代表學習速率,F∈Rm×p,P∈R(n+q)×(n+q)>0為設計參數。

上述觀測器(9)可以寫成下列形式

(11)

(12)

(13)

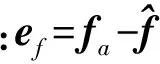
(14)

上述(13)式和(14)式能夠表達為更簡潔的形式

(15)

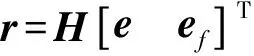
定理1 考慮滿足假設1～2的系統(7),對于給定的正定標量μ,如果存在矩陣P∈R(n+q)×(n+q)>0,LP∈R(n+q)×p和F∈Rm×p滿足下面的不等式[11]

(16)

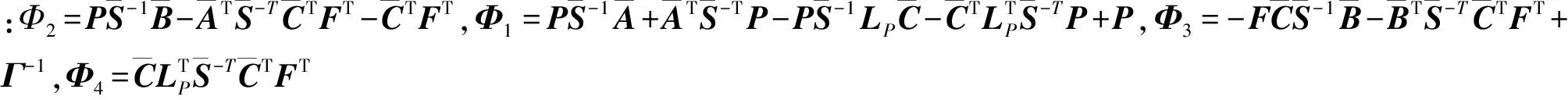
證 定義Lyapunov函數

(17)

(18)

由于不確定項滿足Lipschitz條件,因此

(19)

式中:θ0是一個正定標量,θ0=Lf/‖C‖。

對于任意給定的向量x、y與正定對稱矩陣P,不等式xTy+yTx≤xTPx+2yTP-1y總是成立,因此

(20)

(21)

把(20)式和(21)式帶入(18)式,可以得到

(22)

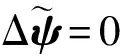
(23)

(24)

(25)

經過簡單的代數運算,(24)式可以寫成

(26)

式中:Λ為不等式(16)的左邊。因此,如果(16)式成立,則J<0一定成立。定理1得證。

注意到不等式(16)是一個非線性矩陣不等式,不能夠應用MATLAB的LMI工具箱進行求解。因此需要做進一步的變換。首先給出相關引理。

引理1 對于適維矩陣Q=QT、F、M、N、不等式(27)Q+εMFN+NTFTMT<0

(27)

對所有滿足FTF≤I的F均成立,當且僅當存在ε>0,不等式(28)成立[12]。

(28)

(29)

(30)

(31)

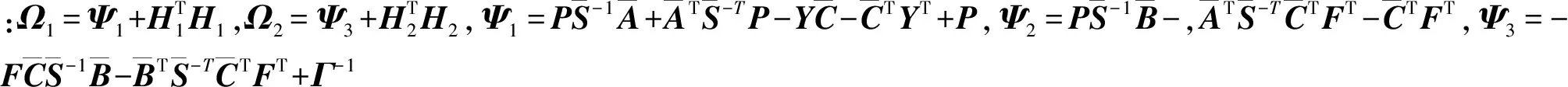
證 具體證明請參見文獻[4,11]。

由于(31)式為等式約束,因此根據線性化算法把定理2轉化為下面的非線性最小化問題[14]。

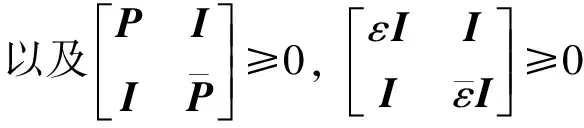
(32)

注3 對于本文采用的故障估計方法,同樣適用于一般的狀態空間模型系統。

3 仿真校驗

考慮系統(5),仿真參數設置如下[12]:衛星轉動慣量:J=diag{18.40,18.20,6.80}kg·m2,軌道角速度ω0=0.001 1rad/s,干擾力矩:Tdx=A0(3cos(ω0t)+1),Tdy=A0(1.5sin(ω0t)+3cos(ω0t)),Tdz=A0(3sin(ω0t)+1),A0=1.5×10-5Nm。應用上述算法,選擇α=600,可以計算得到觀測器的增益矩陣為

3.1 突變型執行機構加性故障仿真結果

假設執行器出現突變型加性故障,故障形式為

(33)

(34)

利用故障估計方法(10)實現對故障(33)～(34)的估計,估計結果如圖1所示。

圖1 執行機構突變故障時響應曲線

從圖中可以看出,在發生故障的情況下,基于魯棒自適應觀測器的故障估計方法能夠在很短的時間內實現對突變故障的精確估計,且由圖中40～80s可知,該觀測器也能實現執行機構無故障時的精確估計。同時也說明,該觀測器能夠同時實現對多方向突變故障的精確估計。

3.2 時變型執行機構加性故障仿真結果

假設執行器出現時變型加性故障,故障形式為

(35)

(36)

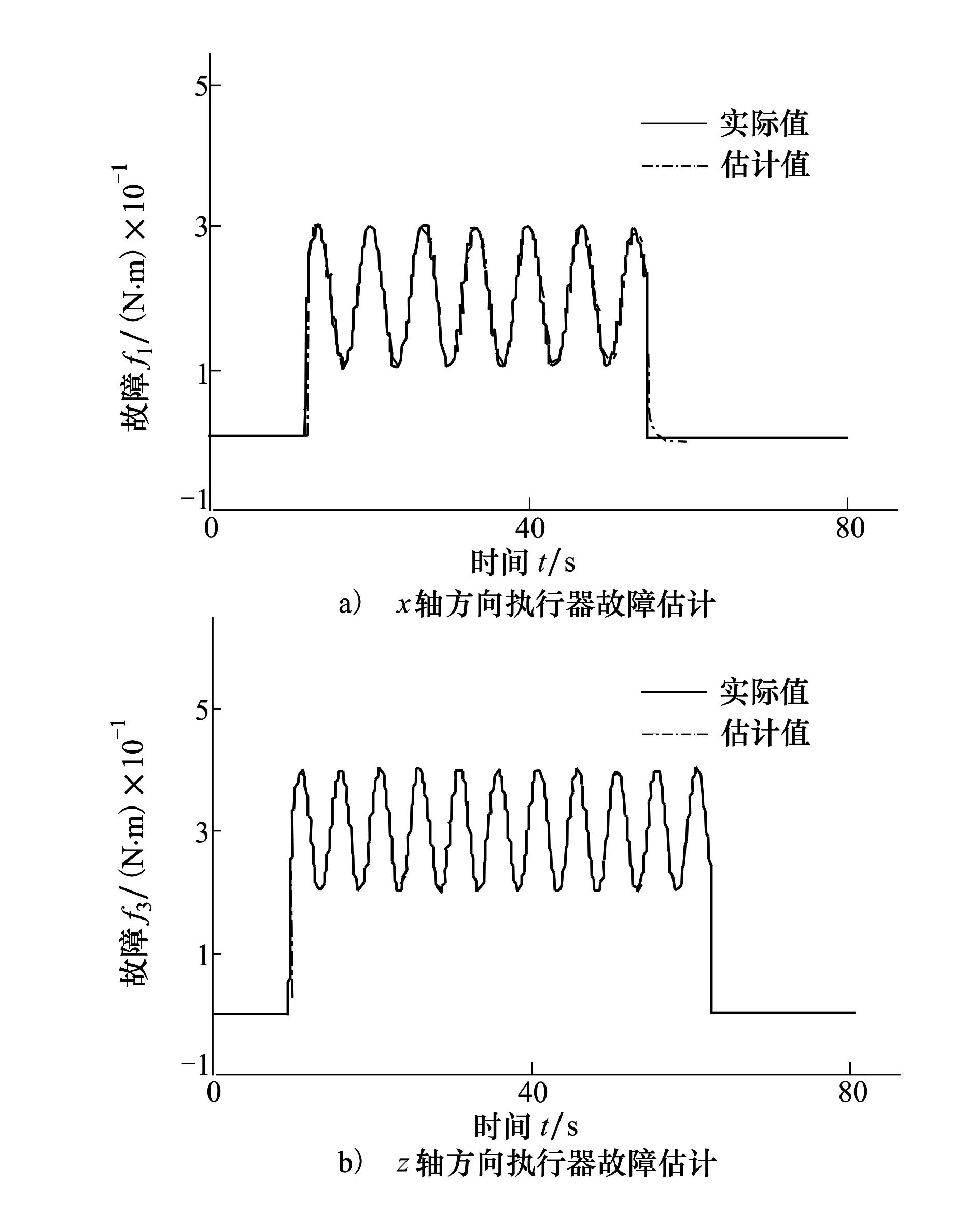
圖2 執行機構時變故障時響應曲線

仿真參數、初始條件如上所述,采用故障估計方法(10)實現對故障(35)～(36)的估計,其仿真結果如圖2所示。從圖中可知,當執行器發生時變故障時,本文采用的故障估計方法能夠在很短的時間內實現對時變型加性故障的精確估計。

3.3 時變型傳感器加性故障仿真結果

假設傳感器出現時變型加性故障,故障形式為

(37)

(38)

仿真參數、初始條件如上所述，采用故障估計方法(10)實現對故障(37)式～(38)式的估計。仿真結果如圖3所示。

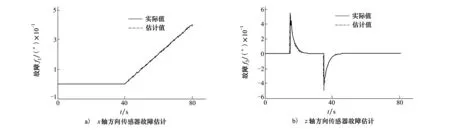
圖3 傳感器時變故障時響應曲線

從圖中可以看出，在傳感器發生緩變故障與指數型變化故障時，本文采用的故障估計方法能夠在很短的時間內實現對時變型加性故障的精確估計。同時也說明，該觀測器能夠同時實現對多方向時變故障的精確估計，且當傳感器與執行器同時發生故障時，該觀測器也能實現對傳感器故障與執行器故障的精確估計。

4 結 論

本文針對具有非結構不確定項的非線性系統中存在的執行器與傳感器故障，采用一種基于描述系統的故障估計觀測器設計方法。該方法能夠在系統存在不確定項干擾的情況下實現對突變故障與時變故障等故障類型的精確估計。仿真實例說明了該方法的有效性。

[1]NguangSK,ShiP,DingS.FaultDetectionforUncertainFuzzySystems:AnLMIApproach[J].IEEETransonFuzzySystem, 2007, 15(2): 1251-1262

[2]ZhangZ,ImadM.Jaimoukha.On-LineFaultDetectionandIsolationforLinearDiscrete-TimeUncertainSystems[J].Automatica, 2014, 50(5): 513-518

[3]FengJ,WangS,ZhaoQ.Closed-LoopDesignofFaultDetectionforNetworkedNon-LinearSystemswithMixedDelaysandPacketLosses[J].IETControlTheoryandApplications, 2013, 7(4): 858-868

[4]ZhangJ,SwainAK,NguangSK.RobustAdaptiveDescriptorObserverDesignforFaultEstimationofUncertainNonlinearSystems[J].JournalofTheFranklinInstitute, 2014, 351(4): 5162-5181

[5]SeyedMT,ThomasB.RobustObserver-BasedFaultEstimationandAccommodationofDiscrete-TimePiecewiseLinearSystems[J].JournalofTheFranklinInstitute, 2014, 35(1): 277-295

[6] 肖冰, 胡慶雷, 馬廣富. 基于觀測器的航天器執行機構失效故障重構[J]. 宇航學報, 2011, 32(2): 1000-1328

XiaoBing,HuQinglei,MaGuangfu.ObserverBasedFaultReconstructionforSpacecraftunderLossofActuatorEffectiveness[J].JournalofAstronautics, 2011, 32(2): 323-328 (inChinese)

[7] 王振華, 沈毅, 張筱雷. 基于增廣觀測器的非線性系統執行器故障診斷[J]. 宇航學報, 2012, 33(12): 1472-1476

WangZhenhua,ShenYi,ZhangXiaolei.AugmentedObserver-BasedActuatorFaultDiagnosisforNonlinearSystems[J].JournalofAstronautics, 2012, 33(12): 1472-1476 (inChinese)

[8] 王振華. 描述系統的故障診斷觀測器設計[D]. 哈爾濱: 哈爾濱工業大學, 2013

WangZhenhua.FaultDiagnosisObserverDesignforDescriptorSystem[D].Harbin,HarbinInstituteofTechnology, 2013 (inChinese)

[9] 張柯. 基于觀測器的動態系統故障估計和調節[D]. 南京: 南京航空航天大學, 2012

ZhangKe.ObserverBasedFaultEstimationandAccommodationforDynamicSystems[D].Nanjing,NanjingUniversityofAeronauticsandAstronautics, 2012 (inChinese)

[10]ZhangJ,SwainAK,NguangSK.RobustSensorFaultEstimationSchemeforSatelliteAttitudeControlSystems[J].JournalofTheFranklinInstitute, 2013, 18(5): 2581-2604

[11]GaoZF,JiangB,ShiP.SensorFaultEstimationandCompensationforMicrosatelliteAttitudeControlSystems[J].InternationalJournalofControl, 2010, 8(2): 228-237

[12] 管宇. 衛星姿態控制系統的故障診斷與容錯方法研究[D]. 哈爾濱: 哈爾濱工業大學, 2012

GuanYu.ResearchonFaultDiagnosisandFault-TolerantControlofSatelliteAttitudeControlSystem[D].Harbin,HarbinInstituteofTechnology, 2012 (inChinese)

Robust Adaptive Fault Estimation for Microsatellite Attitude Control Systems

Zhang Ke1, Han Zhiguo1, Yang Tianshe2, Wang Jingyu1

1.School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.China Xi′an Satellite Control Center, Xi′an 710043, China

This paper using a fault estimation observer design method based on described system, which is subjected to actuator faults and sensor faults in nonlinear systems with unstructured uncertainties. The method has the desired robust performance index, and in the presence of uncertainties, it can achieve accurate reconstructions of abrupt faults and time-varying faults, etc. Sufficient conditions for the existence of the proposed observer have been derived based on Lyapunov stability theory, and then converted into quasi-convex Linear Matrix Inequalities(LMIs) by using the cone complementarily linearization (CCL) algorithm, consecutively using iterative algorithm to get the feasibility solutions. Finally, the performance of the fault estimation scheme derived here is evaluated extensively through applying this method into microsatellite attitude dynamics, which can effectively estimates the actuator faults and sensor faults.

attitude control; linear matrix inequalities; Lyapunov function; fault estimation

2016-04-10

國家自然科學基金(61174204、61101191、61502391)及航天支撐基金(2015KC020121)資助

張科(1968—)，西北工業大學教授、博士生導師，主要從事飛行器導航、制導與控制研究。

V448

A

1000-2758(2016)05-0798-07