課例研究漫談——教學關注思維層次的啟發

☉江蘇省南通市通州區金沙中學季漢杰

課例研究漫談——教學關注思維層次的啟發

☉江蘇省南通市通州區金沙中學季漢杰

數學課堂教學是學生學習數學的主陣地，是啟發學生對數學知識進行理解、記憶、反思、運用的場所.課程標準指出：“數學教學要致力于對學生思維的啟發和培養，將學生的學習從被動接受轉變為主動探索.”課程標準的想法非常美好，但是可以這么說，真正在常態課教學中能做到以啟發思維為主的教學設計少之又少.

大量調查資料顯示，這一教學理念實施非常困難的原因在于：第一，我們教育的現狀是以教師引導下的啟發式為主的教學，以高效課堂為主的教學模式勢必強調了灌輸，從而讓自主思維愈來愈僵化；第二，課程改革和高考改革步調并不一致，課程改革強調自主探索、積極建構，這一方式耗時耗力，勢必延緩教學進度，而高考內容和難度卻一再加深，若長時探索必定浪費時間，造成應試能力的下降.因此，筆者認為，可以在不同的課程類型中使用不同的教學方式，要提高思維層次性，還是要從合理的教學設計入手，螺旋式上升的進行.

一、課例設計

課例絕對值不等式應用案例設計.

思維設計一：已知函數f（x）=|x-a|，g（x）=f（x）+f（x-1）.

（1）若不等式f（x）≤2的解集為｛x|-1≤x≤3｝，求實數a的值.

思維分析：從絕對值最簡捷的相關不等式出發，復習回顧初中數學相關的簡單絕對值不等式的解決方法，并將不等式與方程進行有機結合.這里的思維設計屬于第一層次，即基本知識的回顧和整理.

解析：由f（x）≤2，得|x-a|≤2，解得a-2≤x≤a+2.又不等式f（x）≤2的解集為｛x|-1≤x≤3｝，所以解得a=1.

歸納：|ax+b|≤c，|ax+b|≥c（c≥0）型不等式的解法.

方法一：①若c>0，則|ax+b|≤c等價于-c≤ax+b≤c，|ax+b|≥c等價于ax+b≥c或ax+b≤-c，然后根據a，b的值解出即可；②若c<0，則|ax+b|≤c的解集為?，|ax+b|≥c的解集為R.

方法二：不等式兩邊平方去掉絕對值符號即可.

思維設計二：在（1）的條件下，若對一切的實數x恒有g（x）≥m，求實數m的取值范圍.

思維分析：關注基本問題的發散，教師給出了中學數學恒成立相關基本問題，請學生思考恒成立問題的基本處理方式.當a=1時，g（x）=|x-1|+|x-2|，若對一切的實數x恒有g（x）≥m等價于m≤g（x）min.這里進行的思維設計屬于第二層次，在思維最直接解決不等式問題的基礎上，開發了絕對值恒成立的設計，對于該問題所具備的思維，即在基本思維儲備的基礎上螺旋式上升地提高了知識的運用能力.

解法一：當a=1時，g（x）=|x-1|+|x-2|，于是g（x）=|x-當x>2時，g（x）>1；當1≤x≤2時，g（x）=1；當x<1時，g（x）>1.綜上，對任意的實數x，g（x）min= 1，所以m≤1.

解法二：當a=1時，g（x）=|x-1|+|x-2|，由|x-1|+|x-2|≥|（x-1）-（x-2）|=1，當且僅且當（x-1）（x-2）≤0，即1≤x≤2時等號成立，故對任意的實數x，g（x）min=1，所以m≤1.

說明：①研究含有絕對值的函數問題時，根據絕對值的定義，分類討論去掉絕對值符號，轉化為分段函數，然后數形結合解決是常用的思維方法；②對于求f（x）=|x-a|+|x-b|或f（x）=|x-a|-|x-b|型的最值問題利用絕對值三角不等式更方便.形如f（x）=|x-a|+|x-b|的函數只有最小值，形如f（x）=|x-a|-|x-b|的函數既有最大值又有最小值.這里的解決方式體現了思維設計的兩個方向，第一種方式從分類討論的角度切入，旨在培養學生分類討論的數學思想；第二種方式更是從數學概念、絕對值本質的角度入手思考（即三角不等式的使用），讓問題的解答頗有“山重水復疑無路，柳暗花明又一村”的感覺！

思維設計三：在（1）的條件下，對任意實數b（b≠0）和c，不等式|b|g（x）≤|b+c|+|b-c|恒成立，求實數x的取值范圍.

思維分析：啟迪學生思維，教師在問題設計的時候需要關注一些數學小技巧的處理，此處將恒成立問題進行了深化，將參變分離的思想引入進來，在思維設計二的基礎上進一步提高了不等式恒成立問題解決的思維層次性，實現了設計的層層遞進和思維的循序漸進.當a=1時，g（x）=|x-1|+|x-2|，不等式等價于g（x）≤恒成立，即，即|x-1|+in.因為|b+c|+|b-c|≥|（b+c）+（b-c）|=2|b|，當且僅當（b+c）（bc）≥0時等號成立，所以|x-1|+|x-2|≤

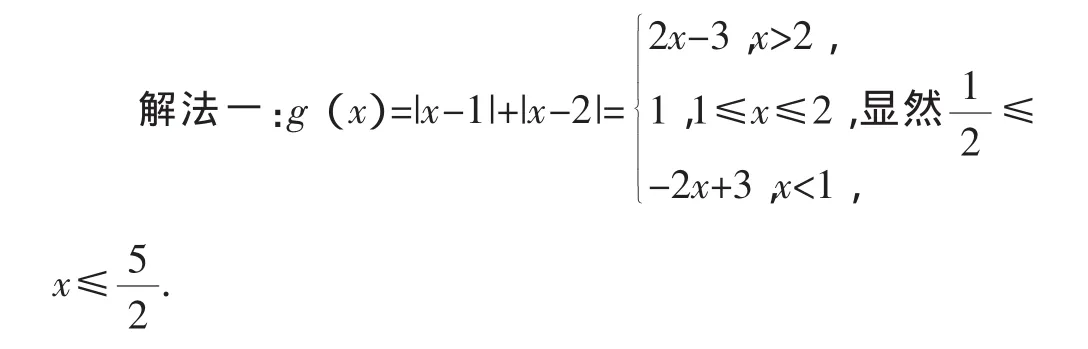
解法二：如圖1，設數軸上與1，2對應的點分別是A，B，則不等式的解就是數軸上到A、B兩點的距離之和小于等于2的點所對應的實數.顯然，區間［1，2］滿足不等式的解集.把A向左移動一個單位到點A1，此時|A1A|＋|A1B|＝0.5＋1.5＝2.把點B向右移動一個單位到點B1，此時|B1A|＋|B1B|＝2，故原不等式的解集為

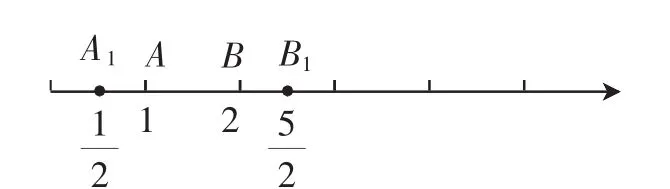
圖1　

解法三：如圖2所示，利用數形結合思想即可.

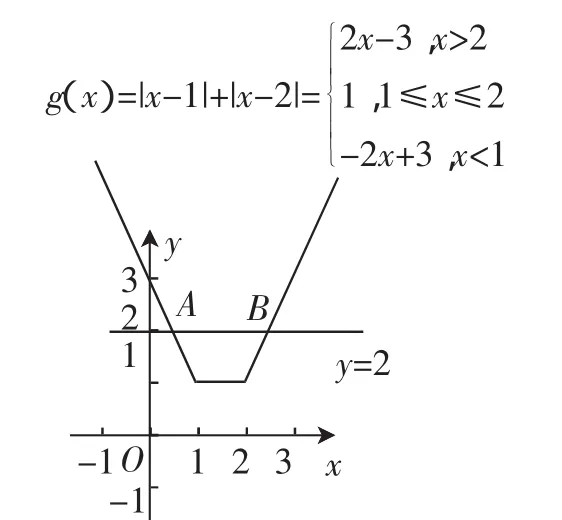
圖2　

說明：形如|x-a|+|x-b|≥c（或≤c）型的不等式主要有三種解法：①分段討論法：利用絕對值號內式子對應方程的根，將數軸分為（（-∞，a］，（a，b］，（b，+∞），此處設a0）的幾何意義：數軸上到點x1=a和x2=b的距離之和大于c的全體，|x-a|+|x-b|≥|（x-a）-（x-b）|=|a-b|.③圖像法：作出函數y1=|x-a|+|x-b|和y2=c的圖像，結合圖像求解.

二、設計反思

回顧上述教學設計，我們看到了教師在引導、啟發學生思維方面做出的三個不同思維設計，這樣的設計符合了層次性原則：

（1）思維設計一是教師教學必須做的基本思維啟發，這種啟發更多的是依賴于知識的回顧，暗示本課所要達到的方向，這種設計盡管較為平淡，也是數學教學最無可厚非的形式化展示.

（2）思維設計二是結合恒成立進行的問題的處理，我們知道恒成立問題對于初學者而言往往是思維混淆的，這里筆者常常借助于一個形象的年齡比喻：將班級某學生甲和某幼兒園所有學生的年齡比大小，我們只要找到甲比該幼兒園中年齡最大的幼兒大即可，即大于最大值；將班級某學生甲和某大學所有學生的年齡比大小，我們只要找到甲比該大學中年齡最小的大學生小即可，即小于最小值.筆者認為，這種思維的形象化啟發是有助于利用非形式化手段闡述形式化的數學過程和結論的，即在學生抽象理解的層面上做到了非常獨到的思維啟發.

（3）思維設計三是恒成立問題的進一步處理，這里筆者想要做的是進一步的思考啟發，即恒成立問題在混亂狀態下的清晰分離.從處理方式來說，參變分離是首選的方法，即將問題轉換為上述年齡問題的理論，這是最好的解決狀態.另外，考慮到絕對值不等式相關的問題還有更為簡捷的距離本質（幾何意義），教師也從這一角度進行了多解性的思考和引導，進一步加深了學生在知識多角度上的思維啟發，可以這么說教師在該節的設計處在了層層遞進的思維上，是較好的思想型課堂.

任何教學設計都存在著一定不足性，筆者課后反思了本課注重思維啟發的設計環節，產生了一些可以繼續優化的教學環節：首先，課堂引入環節的思維設計顯得與后續知識銜接性不足，在指向性上存在著不足，若教師能將后續知識在這里進行基本環節的鋪墊，能更好地體現思維設計一的重要性；其次，絕對值不等式相關的問題類型比較多，這里對于兩種思想方法，即分類討論思想和數形結合思想引入較為到位，但是恒成立問題的設計顯得有些單一，若能更為開放地選擇一些試題，那么既在問題的多樣性上有了實踐探索，又在思維上做到了一定的啟發，這樣的思維設計顯得更為豐滿一些.

總之，現階段教學不能總是以解題重復訓練為主基調，更要從思維訓練的角度進行教學設計，只有關注思維的培養才能將學生的數學素養和能力進行提升，否則，數學學習對于學生而言永遠是一種重復的機械訓練，不利于其思維能力的培養.因此，課堂教學中教師多多關注思維層次性的教學是提高自身課堂教學水平和學生學習能力的關鍵.

1.楊建輝.新課程標準下教師教學設計中應具備的幾種意識［J］.數學通報，2014（2）.

2.冷少華.淺談學生的數學問題意識及其培養［J］.教育探索，2013（6）.