例談幾類解題方法的妙用

☉西安交通大學蘇州附屬中學　蔣亞軍

例談幾類解題方法的妙用

☉西安交通大學蘇州附屬中學蔣亞軍

高中三年的數學知識多而且雜，解題方法往往要綜合和靈活運用函數與方程、轉化與化歸、數形結合、分類與整合、構造法、分離參數法等各種數學思想方法.雖然某些題有一定的解題模式和套路，但又極具靈活性和綜合性，不少題目用常規思路和方法求解，要么過程繁難，要么運算復雜，學生只好“望題興嘆”，因此對不少考生來說，真是“愛恨交加”.筆者結合多年的高三數學專題復習教學，談談幾種解題方法的運用，不當之處，敬請指正.

一、巧用主元法解題

數學中解答多元問題時，如果把它們不分主次來研究，問題很難解決，所謂“主元”方法就是在一個多元數學問題中以其中一個為“主元”，將問題轉化為一元的函數問題，使得在求解最值問題中降低思維難度.

例1已知函數f（x）=3x+a與函數g（x）=3x+2a在區間（b，c）上都有零點，則的最小值為_____.（江蘇省泰州市2014屆高三上學期期末考試數學試卷14）

分析：本題的目標函數有三個變量，這對學生思維增加了很大的難度，若觀察出變量a的最高次數為2，則可將a看成主元將式子變形為二次函數去求解，于是可以收到“避虛就實、變繁成簡，化難為易”的解題效果.

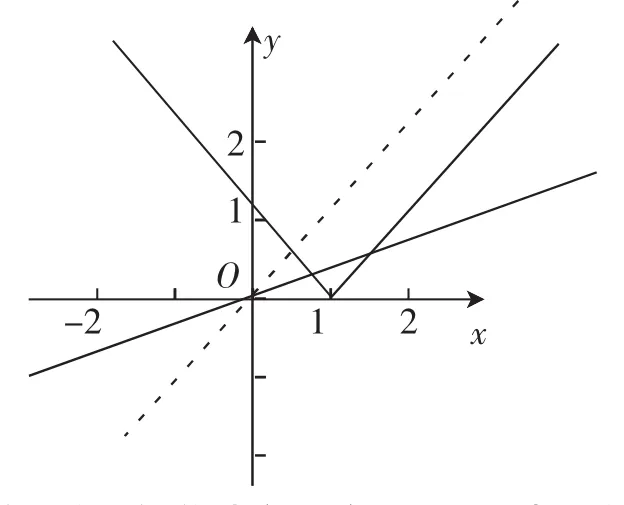
則可得b-c

以上利用主元策略解決了一類“多元”函數最值問題.當我們遇到多元問題時，面對諸多元素，主元策略往往給我們一個頭緒，一條主線，化多元問題為一元問題，體現了化歸與轉化思想.從上述例題中不難看出“主元法”是解題的一種重要的思考方法，我們如能靈活地運用它，就可巧辟捷徑，順利找到合理的解題途徑.利用這種思維策略，對于培養學生良好的思維品質，提高研究問題和解決問題的能力大有裨益.

二、利用辯證法解題

很多學生在解有關函數問題中常出錯的原因主要是不善于運用數學中的矛盾轉化.善于解決數學問題，就是善于運用數學中的矛盾轉化.在解函數問題的中，如果學生能善于用辯證的思維將矛盾轉化，并能夠舉一反三，往往可以很快捷地解決問題.

1.整體與局部的轉化

整體與局部是對立統一的.解題有時從整體考慮可以使我們擺脫對獨立的局部細節的糾纏，使眼界開闊；而有時從局部入手，各個擊破，從而使得整體解決.

例2求函數y=sinx+cosx+sinxcosx的最值.

分析：由于（sinx+cosx）2=1+2sinxcosx，所以可以把sinx+cosx當作一個整體進行換元.令t=sinx+cosx，則1，則容易求出最大值為，最小值為-1.

2.具體與抽象的轉化

數是形的高度抽象，而形是數的具體、形象的表達.數與形之間的轉化本質上就是具體與抽象之間的轉化.華羅庚先生也曾指出“數缺形時少直觀，形缺數時難入微”，這充分揭示了兩者之間相輔相成、相得益彰的辯證關系.

例3對關于x的兩個函數y1=|x-1|和y2=ax（a≠0），若不等式y1≤y2的解集為閉區間［m，n］，其中m

分析：對于此絕對值不等式，常規方法是去絕對值，按x≥1和x<1討論，在每一類中解不等式時又要對a進行討論，過程極其復雜.

利用數與形之間的轉化，即具體與抽象之間的轉化，由數形結合思想分別作出函數y=|x-1|和y=ax（a≠0）的圖像，如圖.

由圖像可知，解集為閉區間［m，n］，當且僅當0

因此，實數a的取值范圍為0

3.已知與未知的轉化

已知與未知是相對而言的，解題時可以根據需要把已知當作未知，也可以把未知當作已知.

例4設a∈R，求關于x的函數y=（a2+1）x2+ax-1的零點最大值和最小值.

分析：函數y=（a2+1）x2+ax-1的零點就是一元二次方程（a2+1）x2+ax-1=0的根，此題的常規方法就是用求根公式求出方程的根，然后求最大值和最小值.這種方法看似可行，但實際操作起來很困難.

從辯證的方法考慮，改變思維方向.我們不妨把a視為未知量，x視為已知量，則原方程可以整理為關于a的一元二次方程x2a2+xa+（x2-1）=0.顯然x≠0（否則得出-1= 0，矛盾），由a∈R知，Δ=x2-4x2（x2-1）≥0，解得.因此，原方程的最大實根為，最小實根

4.相等與不等的轉化

相等與不等是客觀世界的一對矛盾，也是數學中的兩個重要關系.在解題時，相等的問題可以通過不等關系求解，不等的問題也可以轉化為相等關系求解.

例5已知滿足函數y=x2+bx+c的函數值為正的x的集合為｝，求函數y=x2+bx+c的函數值為負的x的集合.

分析：此題直接求解很困難，我們可以考慮相等與不等之間的轉化.從辯證的方法考慮，通過分析問題的整體結構，由條件可知，-2和-是關于x的方程x2+bx+c=0的兩個根，則由韋達定理可知，進而易求得所求函數y=x2+bx+c的函數值為負的x的集合為

通過對解決函數問題中體現出來的辯證法思想的系統歸納和總結，能夠使學生從中學會用聯系的、運動變化和發展的觀點觀察和思考問題.與此同時，由于對辯證法這種科學的思想方法的了解和掌握，又可以反過來指導學生的思想和行動，從而也相應地提高了他們正確地分析函數問題和解決函數問題的能力.

三、巧用放縮法解題

函數壓軸題是一個熱點，其中一類常見函數問題是證明函數不等式或者根據函數不等式恒成立求參數的范圍.這類問題綜合性強，思維量大，能力要求高，大部分學生在碰到這類問題時感覺困難，無從下手.而“放縮法”是解決這類問題的有效手段，但在放縮過程中，又會常常出現思維受阻的現象，此時我們不僅需要熟悉一些常見的函數不等式，而且還要掌握一些常見的基本放縮方法，明確放縮點.

1.直接放縮法

（1）求f（x）的單調區間和極值.

（2）是否存在實數a，使得關于x的不等式f（x）≥a的解集為（0，+∞）？若存在，求a的取值范圍；若不存在，試說明理由.

解：（1）略；

所以當a≤0時，關于x的不等式（fx）≥a的解集為（0，+∞）.

②當a>0時，下面先證明不等式：當x≥4時，lnx<

綜合①②知，存在a，使得關于x的不等式f（x）≥a的解集是（0，+∞），且a的取值范圍是（-∞，0］.

點評：一般先分析函數的特點，看是否具有某些明顯的性質.這里先通過觀察發現，可對函數變形說明f（x）>0恒成立，然后只要再舉例說明對任意大于零的數a，存在x∈（0，+∞）使得f（x）-1）和對函數f（x）進行了放縮.這兩個不等式中前一個不等式是我們所熟悉的，后一個不等式根據我們方便求解的需要可以通過聯想指數、對數、冪函數的增長快慢想到.這里我們可通過直接對函數放縮進行求解，不妨稱之為直接放縮法.

2.先求導后放縮法

例7設函數f（x）=ex-1-x-ax2.

（1）當a=0時，求f（x）的單調區間；

（2）若當x≥0時，f（x）≥0，求a的取值范圍.

解：（1）略.

（2）f′（x）=ex-1-2ax，由（1）知，ex≥1+x，當且僅當x=0時等號成立.所以f′（x）≥x-2ax=（1-2a）x，從而當1-2a≥ 0，即a≤時，f′（x）≥0（x≥0），又f（0）=0，所以當x≥0時，f（x）≥0.

由ex>1+x（x≠0）可得e-x>1-x（x≠0），從而當時，f′（x）

點評：對比較復雜的含有指數，對數的函數表達式，當不能觀察出某些明顯性質時，可先嘗試求導再觀察.這里對f（x）求導后，利用不等式ex≥1+x對導函數進行放縮，得到使f（x）≥0成立的一個必要條件，然后再利用不等式e-x>1-x（x≠0）對導函數進行放縮說明當a>時，f（x）≥0不恒成立，從而求出a的取值范圍，這里采取的方法是先對函數求導再對導函數進行放縮求解，不妨稱之為先求導后放縮方法.

3.先放縮后求導法

碰到證明函數不等式或求函數中的參數取值范圍時我們往往會采取先求導后放縮得的方法來處理，但有時候我們反過來采取先對函數進行放縮再來求導會事半功倍.

（1）求a，b的值；

證明：（1）易得a=0，b=-1.

所以g（x）在（0，2）內單調遞增.

點評：對比較復雜函數求導后發現任很復雜不好處理時可以回過頭來再仔細觀察能不能先對函數進行化簡或放縮.這里如果直接構造函數，求導數，導函數既含有無理式又含有分式比較復雜，所以想到先用不等式把根式去掉，把f（x）放大：f（x）=ln（x+1）+，再把問題轉化為證明ln（x+1）+成立，這樣使問題迎刃而解.這里用到的方法是先放縮再構造函數求導證明，非常簡潔，不妨稱之為先放縮后求導法.該問題也可以采取先求導再放縮法，利用ln（x+1）≤x和對導函數進行放縮來判斷導函數的符號，進而證明（在此不再贅述）.

對函數進行放縮是我們求解有關函數問題的一種常用方法，在采用放縮法時，我們要用扎實的知識和一定的能力，能根據問題的特點以及函數結構，在相關知識的指導下，找準放縮點，找到放縮不等式，這樣才能達到避繁就簡、化難為易、事半功倍的效果.

以上僅僅列舉了三種常見的解題思想，在實際教學實踐中遠不止這些，只要我們肯觀察，常動腦，就會有意想不到的收獲.