立體幾何問題的解答中圖形的構造技巧

☉河南大學附屬中學　（23中）張一廿

立體幾何問題的解答中圖形的構造技巧

☉河南大學附屬中學（23中）張一廿

在立體幾何客觀題中常涉及一些求距離、角度、面積、體積問題，但與這些問題相關的點、線、面的位置關系并沒有明確給出，需要我們結合題目條件準確構造出這些對象所在的位置.那么具體問題中應如何構造，這是問題能否順利求解的關鍵.本文以2016年一道高考題為引例，就其中所涉及的構造思想進行分析.

引例（2016全國I卷）平面α過正方體ABCD-A1B1C1D1的頂點A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，則m，n所成角的正弦值為（）

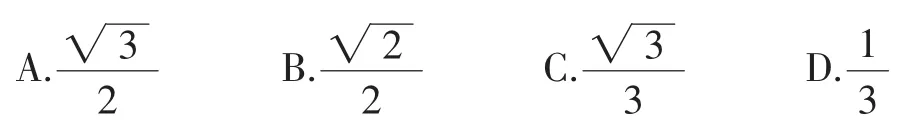
題目條件中面α的位置沒有明確給出，因此涉及的兩條線m，n的位置也不確定.那么應如何構造出過頂點A且與面CB1D1平行的平面α，是問題求解的關鍵.下面從兩種視角來構造平面α，來實現問題的簡潔求解.

解法1：如圖1，延長D1A1至點D2，使A1D2=D1A1.延長B1A1至點B2，使A1B2=B1A1，連接B2D1，B2D2，AB2，AD2，B1D2，

易知B2D2∥=B1D1，AB2

∥=CD1，AD2

∥=CB1，所以平面AB2D2∥面B1CD1，所以面AB2D2即為題目中的面α，AB2即為直線m所在的位置，B2D2即為直線n所在的位置.

又因為CD1，CB1，B1D1均為正方體ABCD-A1B1C1D1的面對角線，所以CD1=CB1=B1D1，所以B2D2=AB2=AD2，即△AB2D2為等邊三角形，則m，n所成角即為AB2與B2D2的夾角，其大小為，故其正弦值為

圖1　

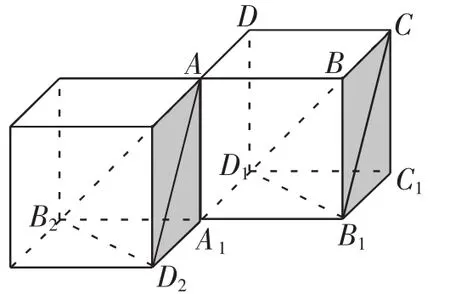
解法2：構造與正方體ABCD-A1B1C1D1相連的正方體，如圖2所示，則條件中所求的各對象直觀地展現在我們面前，易知面AB2D2即為已知條件中的α，則m，n的位置相應地確定了.故可直接得出正確答案.

點評：本題的求解關鍵是根據題目特征，找到所求的面，進而將所求關系明確化，使問題簡潔獲解.

除此之外，在某些問題中，與題目相關的點、線、體等條件的確定是問題順利求解的重要保證，下面舉例說明.

一、構造定點

例1如圖3所示，正方體ABCDA1B1C1D1的棱長為1，BD∩AC=O，M是線段D1O上的動點，過點M做平面ACD1的垂線交平面A1B1C1D1于點N，則點N到點A距離的最小值為（）

圖3　

解析：本題求動點N到定點A的距離的最小值，關鍵是確定點N所在的位置.

如圖4，連接B1D1，根據題目條件易知平面ACD1⊥平面BDD1B1，而NM⊥平面ACD1，即NM⊥OD1，所以NM的面BDD1B1內，所以點N的軌跡為面BDD1B1與面A1B1C1D1的交線B1D1上.連接AB，易知△AB1D1為等腰三角形，故當N為B1D1的中點時，NA的距離最小，易求得最小值為.故選B.

圖4　

點評：本題求解的關鍵是確定點N所在的位置，即點N在線段B1D1上運動，進而將問題轉化為點到線的最短距離，易知AN⊥B1D1時，距離最小.

二、構造定線

例2在邊長為2的正方體ABCD—A1B1C1D1中，E為BC的中點，點M在底面ABCD上移動，且滿足B1M⊥D1E，則線段B1M長度的最大值為（）

解析：因為點M為動點，但B1M⊥D1E，故B1M在與D1E垂直的平面內.

如圖5，設CC1的中點為N，因為B1N與BC均在面BCC1B1內，所以B1N與BC所在的直線相交，設交點為S，連接AS.又因為點S在ABCD所在的平面內，所以AS與CD相交，設交點為O.

連接AB1，由三垂線定理易證D1E⊥AB1.

連接C1E，易證B1N⊥C1E，而C1D1⊥B1N，

所以B1N⊥平面C1D1E，所以B1N⊥D1E.

綜上，D1E⊥平面AB1S，即點M在線段AO上.

又因為△SCN～△SBB1，△SOC～△SAB，

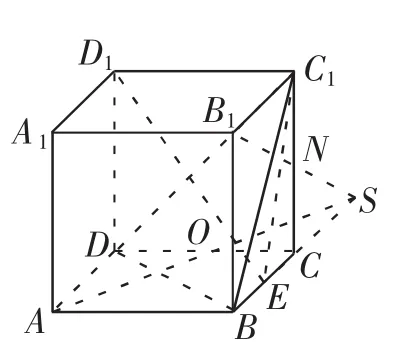
圖5　

評析：本題的求解關鍵是確定動點M所在的定線的位置.對于動態問題的解答要善于把握其中不變的因素，如本題中點M為面ABCD內的動點，但B1M⊥D1E，因此B1M在一個與D1E垂直的定面上，找到這個定面即可順利找到動點M所在的直線.另外題目中若涉及一條動直線與已知平面平行，則動直線在與已知面平行的定面內.解題中只要抓住這些動態問題中的確定因素，就可順利找到問題的切入點.

三、構造定面

例3如圖6所示，在正方體ABCD-A1B1C1D1中，點E是邊BC的中點，動點P在直線BD1（除B，D1兩點）上運動的過程中，平面DEP可能經過的頂點是_______（寫出滿足條件的所有頂點）.

解析：由題意知，平面DEP過點D.

若平面DEP過點A1，如圖7所示作平面A1DE，與BB1交于點F，DF與BD1在平面BDD1B1內，則DF與BD1的交點即為點P，故平面DEP過點A1.

若平面DEP過點B1，如圖8所示作平面B1DE，與A1D1交于點F，DB1與BD1在平面BDD1B1內，則DB1與BD1的交點即為點P，故面DEP過點D1.

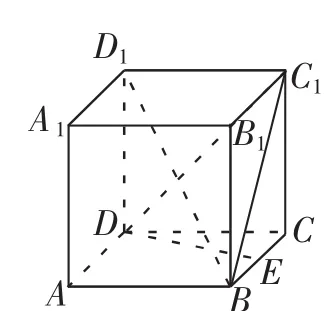
圖6　

若面DEP過點C1，如圖9所示作面C1DE，由圖易知DC1與CD1在面CDD1C1內，設DC1與CD1交于點F，則易知點F為CD1的中點.連接EF，所以EF為三角形BCD1的中位線，所以EF平行于BD1，即面DEC1與BD1沒有交點，所以滿足條件的點P不存在，所以面DEP不經過點C1.

綜上所述，正確答案為A1，B1，D.

圖7　

圖8　

圖9　

點評：本題若直接作面DEP，看其過哪些頂點，則陷入誤區.轉換問題求解視角，即選擇某個頂點，結合D、E構造平面，只要保證所作平面與BD1相交，則該頂點符合要求.

四、構造定體

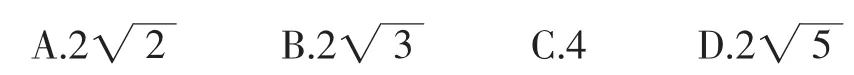
解析：根據題目條件可構造符合條件的長方體，通過長方體的體對角線在三個面上的投影來實現對問題的解答，即利用長方體的體對角線和面對角線列出方程組，轉化為a和b的關系，再根據a和b關系確定最大值.具體解答過程如下：

根據題意，如圖10所示，設長方體的長、寬、高分別為m、n、k，則

圖10　

所以（a2-1）+（b2-1）=6，即a2+b2=8.

所以（a+b）2=a2+2ab+b2=8+2ab≤8+a2+b2=16，

即a+b≤4，當且僅當a=b=2時取等號.所以當a=b=2時，a+b取最大值4.

評析：對于某些空間幾何體問題中，如果涉及幾何體的三視圖，常用的解題策略是根據三視圖，構造相應的特殊幾何體，如長方體、正方體等，能給問題的解決帶來便利.本題解答中通過聯想、構造，將問題轉化為長方體的一條體對角線在三個面上的投影問題，降低了難度，使問題得到順利解決.