基于啟發式規則的臨時分段調度計劃與優化

張志英,曾建智

( 同濟大學 機械與能源工程學院，上海 201804)

?

基于啟發式規則的臨時分段調度計劃與優化

張志英,曾建智

( 同濟大學 機械與能源工程學院，上海 201804)

船舶堆場中臨時分段調度方案的優劣影響著調度的效率和成本。本文以臨時分段的調度過程為優化對象，以平板車的移動距離為優化目標建立數學模型。通過制定動態的臨時分段調度規則和超長分段調度規則，充分利用堆場中的空存儲單元，最終確定一個較優的臨時分段調度方案。同時利用任務合并對堆場調度的任務序列進行優化，從而減少調度過程中臨時分段的數量。最后，利用某船廠的實際數據對模型和調度規則進行實例驗證和數值分析，結果表明，所制定的調度規則可以優化堆場調度方案，提高堆場空間資源利用率和調度效率。

堆場；調度規則；超長分段；任務合并；啟發式規則

在大中型船舶的設計階段，因為生產資源和工藝的約束，一艘船通常被分割為200個左右的分段，這些分段分別進行獨立的生產建造，最后在船塢進行搭載。由于船舶企業生產和管理的原因，各個分段在不同加工工序之間無法即時周轉，堆場便作為暫存或者預處理(預舾裝、檢驗和修補等)分段的場所。作為中間產品的分段規格約為15 m×15 m×5 m，重量為100～300 t，有些特殊規格的分段甚至超過500 t。因此需要專門的搬運設備(平板車)對分段進行運輸和調度。平板車只能進行平面方向上的運輸，且一次只能搬運一個分段，它利用液壓裝置將分段提升，通過堆場中的可行路徑，將分段移動至目標位置并放置支撐桿上。在船舶堆場調度過程中，根據作業流程可分為三種分段：進場分段、出場分段和臨時分段。對于臨時分段的處理是無增值的操作，且對其采用不同的調度規則會直接影響平板車的調度效率以及整個堆場的調度計劃，因此對于臨時分段如何制定一個科學、合理的調度規則尤為重要。

分段堆場一般為若干個大小相等的正方形場地組成的一個矩形區域，每一個場地為一個存儲單元。一個存儲單元一般存放一個分段(常規分段)，但是船舶分段的尺寸不盡相同，對于一些超長規格的分段，將占用一個以上的存儲單元。這些分段成為臨時分段時，其調度復雜程度將遠遠大于常規分段，堆場需要為其制定相應的調度方法。Changkyu等[1-2]以臨時分段移動數量為優化目標建立模型，并運用遺傳算法和改進動態啟發式算法對模型進行求解。Tao等[3]在此基礎上考慮分段進出堆場任務順序對調度方案的影響，并運用啟發式算法和禁忌搜索對結果進行優化。以上研究通過制定相應的規則對臨時分段的位置進行重新選擇，雖然提高堆場的空間利用率，但是臨時分段可能阻礙其他分段的移動，增加了調度難度且效率不高。申鋼等[4]以最小化臨時分段移動量和平板車在堆場中的行駛距離為優化目標建立優化模型，并運用分支定界法和啟發式規則來確定分段的移動路徑和停放位置。平板車移動路徑中的臨時分段先移至堆場外暫存，待分段調度完成后再移回原來位置。徐建祥等[5]提出利用臨時場地用于暫時存放臨時分段并在任務結束后移回原來位置。以上研究對臨時分段都采用了重回原位的調度策略，對堆場空存儲單元并沒有充分的利用，堆場調度過程是一個靜態的過程，堆場的空間資源利用率不高。而且每一個調度任務結束后都需將暫存在堆場外的臨時分段移回，可能再次影響后續的調度任務。對于特殊規格分段的研究，Tao[6]考慮了超重分段的調度，當分段重量大于平板車的額定載重時，采用兩輛平板車協同調度的方法并制定了相應的平板車指派規則，但其研究的是船廠中車間與車間和車間與堆場之間的調度流程優化，并沒有對堆場內部的調度進行細化的研究。

本文通過對臨時分段的調度過程進行研究，提出動態的臨時分段調度規則，并針對超長分段，研究相應的調度方法。同時還對調度時間差在規定可接受時間范圍內的任務進行任務合并，最終得到一個科學、合理的堆場調度方案，并用某船廠的實際數據對以上調度規則的合理性進行驗證。

1 問題描述與解決方法

1.1 問題描述

船舶分段堆場的調度與集裝箱堆場的調度[7]相似，但其屬于平面調度[8]。分段堆場的調度操作包括分段的存放和取回，由于平板車運輸的局限性[9]，在存放和取回分段的路徑中會遇到阻擋其前進的分段(臨時分段)，必須將這些分段移動至平板車調度路徑之外，才能完成后續的調度工作。對于臨時分段的處理一般有移至暫存場所待分段調度完成后移回原位和移至堆場的其他空存儲單元進行存放。但這兩種方法都需要將臨時分段移出堆場，使得平板車的移動距離較遠、調度時間較長，從而導致堆場的調度效率不高。因此需要對臨時分段的調度方法進行優化。

船舶設計過程中由于建造工藝要求特殊[10]，船舶艏、艉部的分段其規格與大部分常規分段有所不同，其中有部分超長分段，這些分段需要占用的存儲單元數較多且連續，更容易成為臨時分段。因此需要根據分段的形狀特性來進行相應的調度。

分段堆場調度中每一個分段都有其相應的調度時間，而由于堆場空間資源的有限性，一些調度時間較晚的分段不可避免的會存放于調度時間較早分段的移動路徑上，成為了臨時分段。這樣在調度過程中會產生大量不必要的臨時分段，從而增加了堆場的運作成本。

考慮到堆場運作的實際情況和研究問題的方便，作了以下假設：1)船舶分段堆場由若干個面積相等的正方形場地組成，每個正方形場地為一個存儲單元；2)分段用最小包絡矩形近似；3)一個存儲單元只能存放一個分段；4)每個存儲單元能容下各種常規分段；5)超長分段需要兩個相鄰的存儲單元進行存放；6)調度時間差在可接受范圍內的調度任務可以進行任務合并；7)所有分段按“筆直型”路徑進出堆場。

根據以上假設，本文擬解決的問題有：1)確定堆場調度計劃中所產生臨時分段的具體調度過程；2)調度過程中超長分段的調度方案；3)對計劃調度周期內分段的調度任務序列進行優化。

1.2 解決方法

本文針對以上問題，首先研究了臨時分段動態的調度規則，對臨時分段采取移動至相鄰的空存儲單元的調度方法；其次對于超長分段也提出了相應的調度規則，通過平板車的旋轉、平移等操作對超長分段進行調度；最后以臨時分段移動距離為優化目標，利用以上調度規則優化堆場一段調度時間內的調度過程。本文還根據堆場的實際情況，對調度時間相近的任務進行任務合并，優化堆場分段調度計劃的任務序列。分段調度流程如圖1所示。

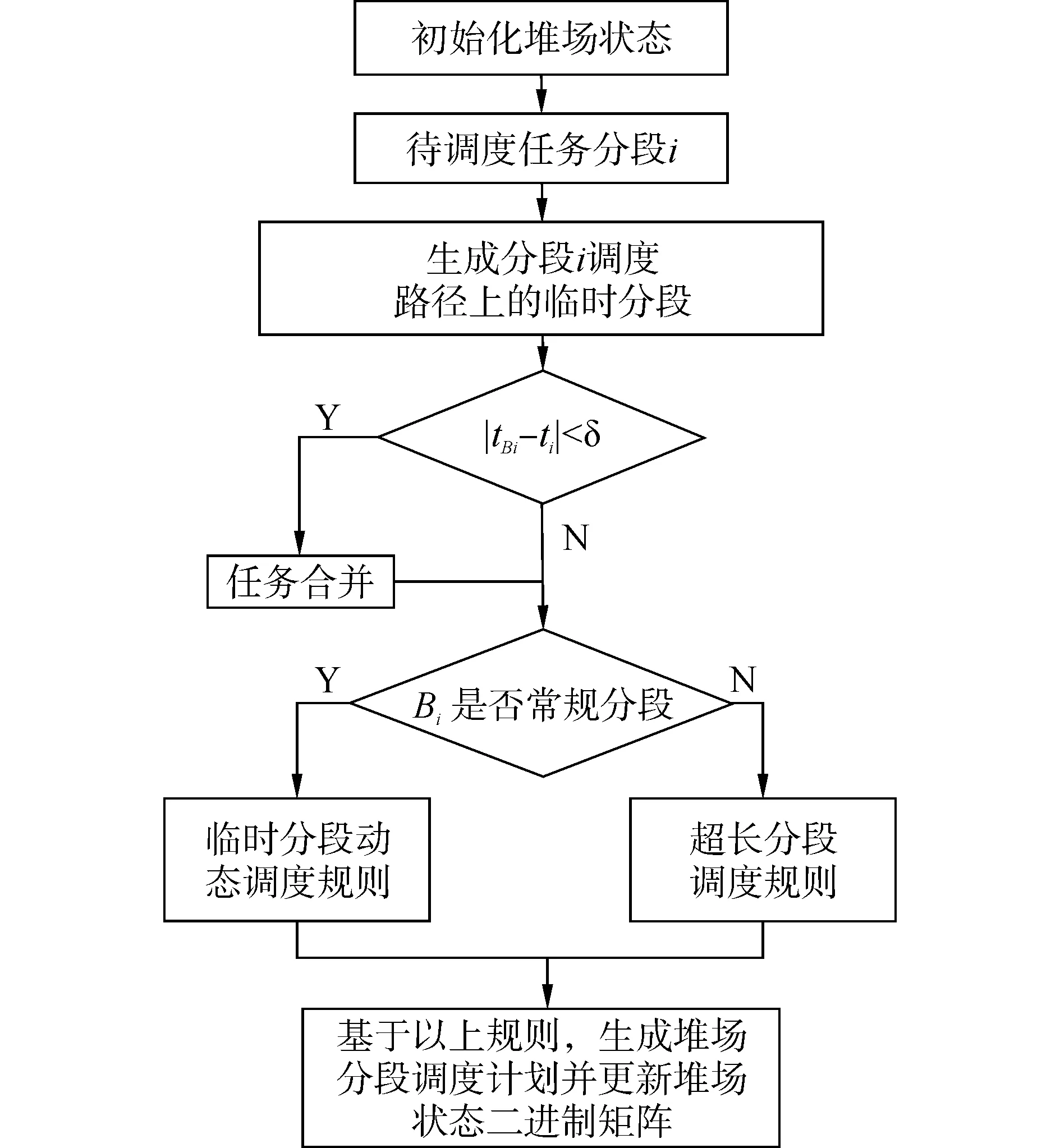
圖1 分段調度流程圖Fig.1 Block scheduling flow chart

2 建立船舶分段堆場調度模型

2.1 分段堆場存儲單元位置編碼

船舶分段堆場由若干個大小相同的正方形場地組成，每一個場地為一個存儲單元。存儲單元的位置編碼方式為臨近道路的位置開始從左至右，從上至下依次編碼，如圖2所示，堆場被劃分成M行N列，即堆場有M×N個存儲單元，存儲單元位置編碼從1至M×N。

圖2 存儲單元位置編碼Fig.2 Position coding of storage unit

2.2 堆場狀態二進制矩陣

為了表示分段在堆場中的停放位置及堆場存儲單元的狀態，建立堆場狀態二進制矩陣。矩陣Ht的每個元素bVi表示調度時刻t堆場中存儲單元位置為Vi的狀態，bVi=1表示存儲單元內已有分段存放，bVi=0表示該時刻存儲單元狀態為空。

2.3 堆場狀態的更新

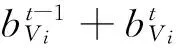
2.4 堆場調度模型

模型中的符號如下：

M、N分別表示堆場在寬度和長度上被劃分的存儲單元數量，堆場中存儲單元的總數為M×N；

D：堆場存儲單元的規格D×D；

W：堆場至暫存堆場的距離；

(Lg，Wg)：分段g的幾何投影參數，其中g∈R；

T：堆場的調度周期；

ts：調度周期T的開始時間；

te：調度周期T的結束時間；

Vi：分段i在堆場中的位置；

tRi：分段Ri的調度時間；

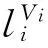
決策變量：

目標函數：

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

目標函數(1)根據不同規格的分段計算出堆場每次調度時臨時分段的移動距離，并利用所對應的調度規則選擇每個臨時分段的最優調度方法，使整個調度周期內，對于臨時分段平板車的移動距離最小。同時，根據任務合并的規則，對整個調度計劃內的任務調度序列進行優化。

約束(2)限制堆場每次只能執行一個調度任務；約束(3)限定臨時分段與調度分段之間的相互位置關系；約束(4)表示超長分段的尺寸與存儲單元大小的關系；約束(5)、(6)規定了不同規格類型的分段所分配的存儲單元個數，即常規分段分配一個確定的存儲單元，超長分段需要兩個相鄰的存儲單元才能滿足其存放空間需求。約束(7)確保分段的調度時間在規定的調度周期內。

3 基于啟發式規則的堆場調度模型求解

3.1 臨時分段動態調度規則

現有堆場調度對于臨時分段的處理一般將其移至堆場外的暫存堆場，等調度結束后再將分段移回原位。這樣的調度方法不僅平板車移動距離遠，而且占用堆場以外的其他資源。將臨時分段重新選位能有效的提高對堆場資源的利用率，但是該調度方法較為繁雜。因此，本文對臨時分段采取動態的調度規則，即利用臨時分段相鄰的空存儲單元進行合理調度。

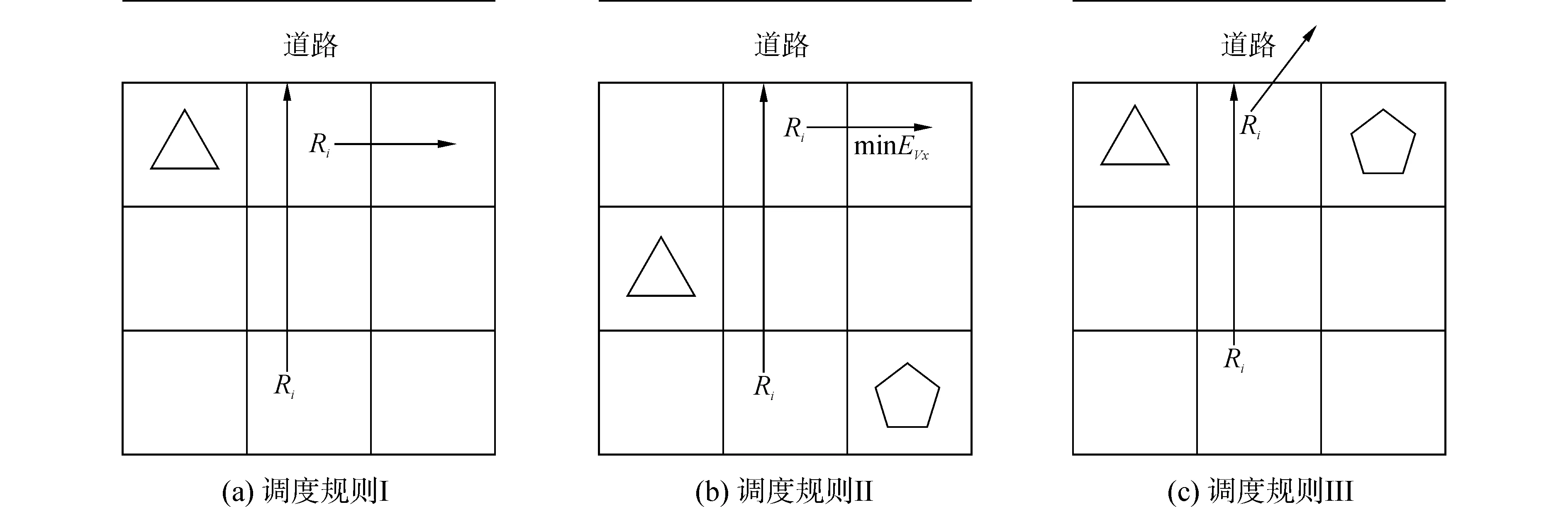
圖3 臨時分段調度規則Fig.3 Scheduling rule of the obstructive blocks

3.2 超長分段調度規則

對于超長分段的存放位置VSi作以下規定：若超長分段Si平行于道路存放(pSi=1)，那么該分段的存放位置用分段左端所占的存儲單元位置表示；若超長分段Si垂直于道路存放(pSi=0)，則該分段的存放位置用分段上端所占的存儲單元位置表示。

平板車在堆場中除了平移，還可以通過旋轉操作將超長分段以OSi為中心進行旋轉，從而完成后面存儲單元上存放分段的調度任務。若分段調度路徑中存在超長分段，即臨時分段為超長分段的情況，為此提出以下調度規則：

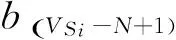
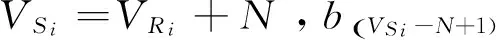
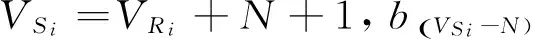
5)超長分段垂直于道路存放，即pSi=0，則按照常規分段的調度規則對其進行調度。

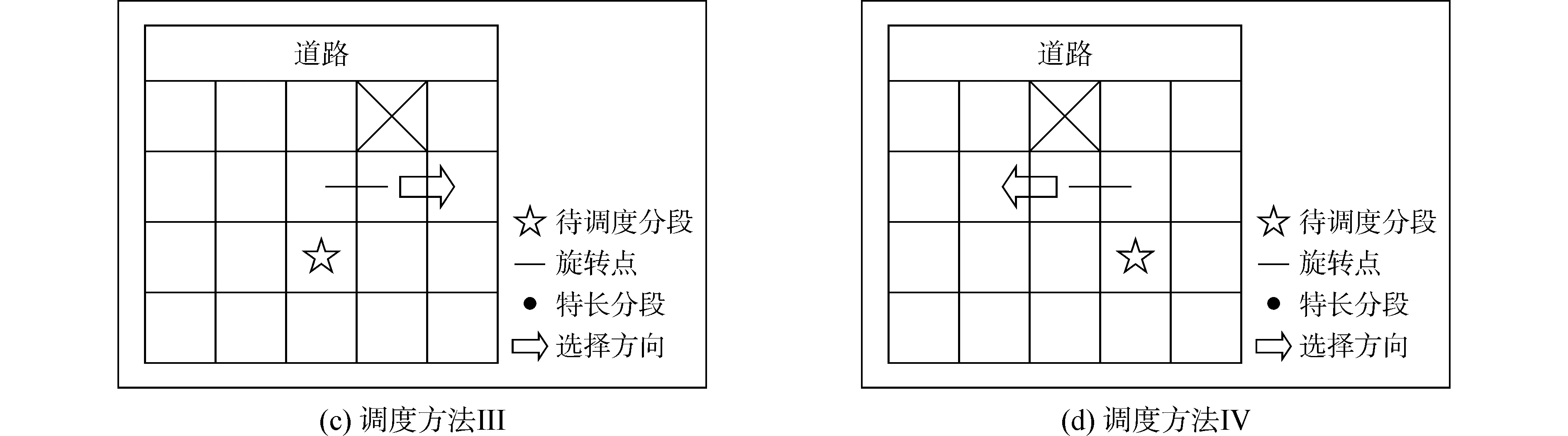
圖4 超長分段調度方法Fig.4 Scheduling method of the ultra-long blocks

3.3 任務合并規則

在堆場中兩分段Ri與Rj，若在調度中存在以下關系：分段Rj在分段Ri的移動路徑上，且分段Ri的調度時間早于分段Rj。這樣分段Rj便成為了臨時分段，需要利用平板車將其移動至其他位置來完成對分段Ri的調度。但若這兩個調度分段的調度時間差在一個可以接受的時間范圍δ內，便可以將這兩個調度任務合并，即忽略兩者的調度時間順序，根據它們的存放位置關系依次進行調度。如圖5所示。

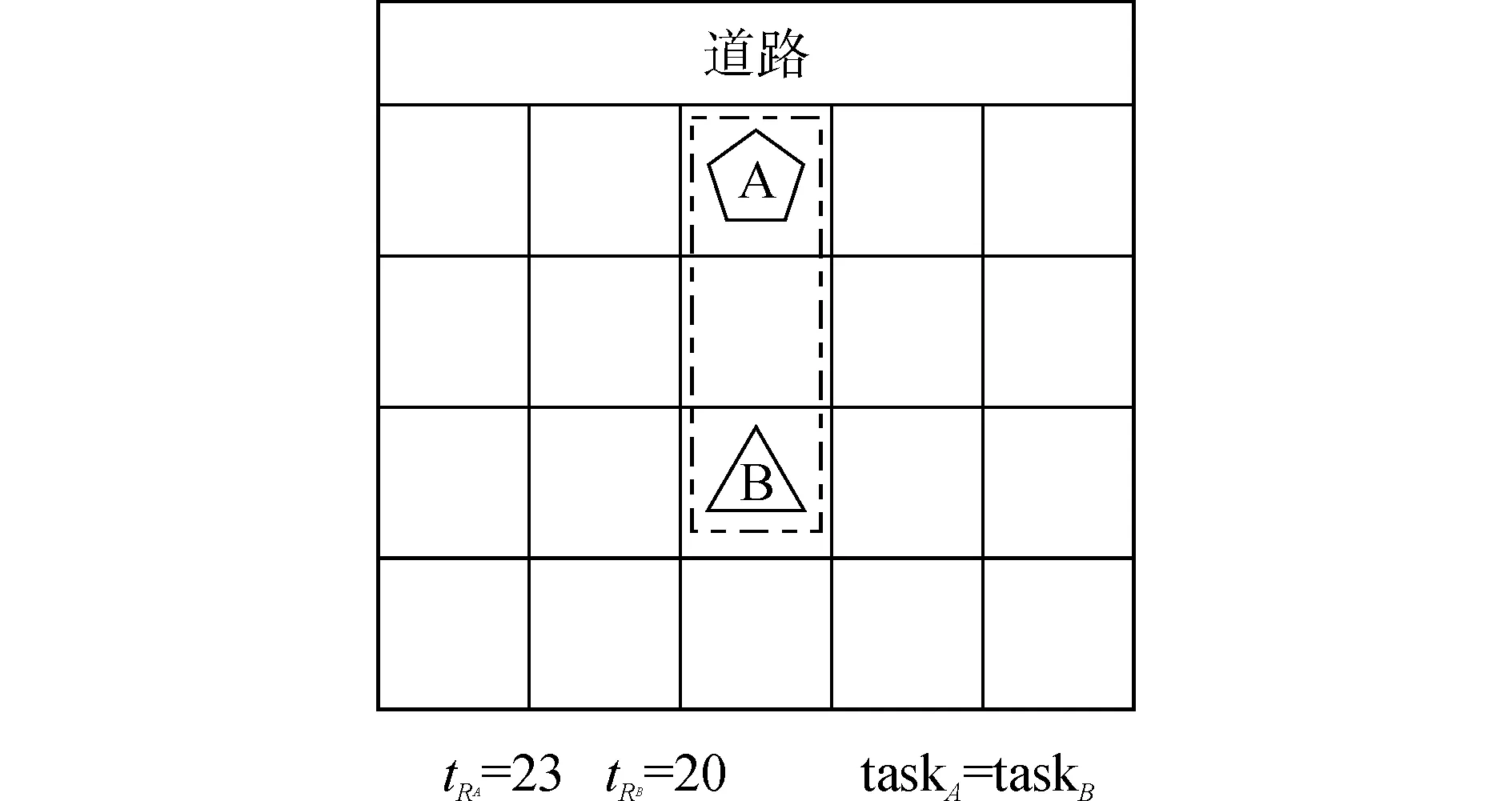
圖5 任務合并示例Fig.5 Task merging sample

(8)

(9)

(10)

(11)

式(8)表示兩調度分段之間的時間約束關系；式(9)、(10)說明了兩調度分段之間的位置關系；式(11)限定兩個任務合并的分段的調度時間差必須在δ內，否則兩個任務不能合并。滿足以上條件的任務可以進行合并，即taski=taskj。

4 實例驗證與結果分析

4.1 實驗驗證與結果

為了驗證本文調度模型以及規則的可行性與正確性，以上海某大型船廠調度周期內一段時間的分段調度為例，利用MicrosoftVisualStudio2010軟件，在處理器為2.40GHz，內存為4GB的計算機上進行求解。實驗包括以下輸入參數：1)堆場調度前的二進制狀態矩陣；2)60h內所需調度的分段及其具體調度時間(表1)；3)堆場調度允許任務合并的最大時間差δ=3h。某堆場調度前的狀態如圖6所示，堆場的參數為M=6，N=10，即堆場由60個存儲單元構成，初始負載率為65%，Bx是已存放在堆場存儲單元上分段的編號。

按照調度時間順序排列的調度計劃如表1所示，調度分段的數量為30個，其中進場分段13個(常規分段用A1至A10依次編號，超長分段用S1至S3編號)，出場分段17個(用Bx表示)，為了便于區分，調度過程中遇到的臨時分段用Bx表示。

通過算法程序確定調度分段進出堆場時所產生的臨時分段，用本文研究的調度規則對臨時分段、超長分段的具體調度過程進行優化，同時將任務合并的規則運用到調度中，得到一種較優的堆場臨時分段調度方案，如表2所示，其中陰影部分表示任務進行了合并，任務合并減少的臨時分段由△表示。若取D=15m、W=10m，該調度方案的臨時分段移動距離為656.3m，其中平板車對超長臨時分段進行了3次旋轉調度操作，采用任務合并后臨時分段數量減少了9個。

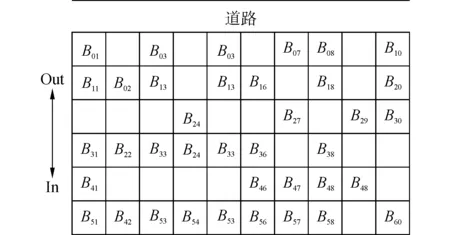
圖6 堆場初始狀態Fig.6 Stockyard initial state

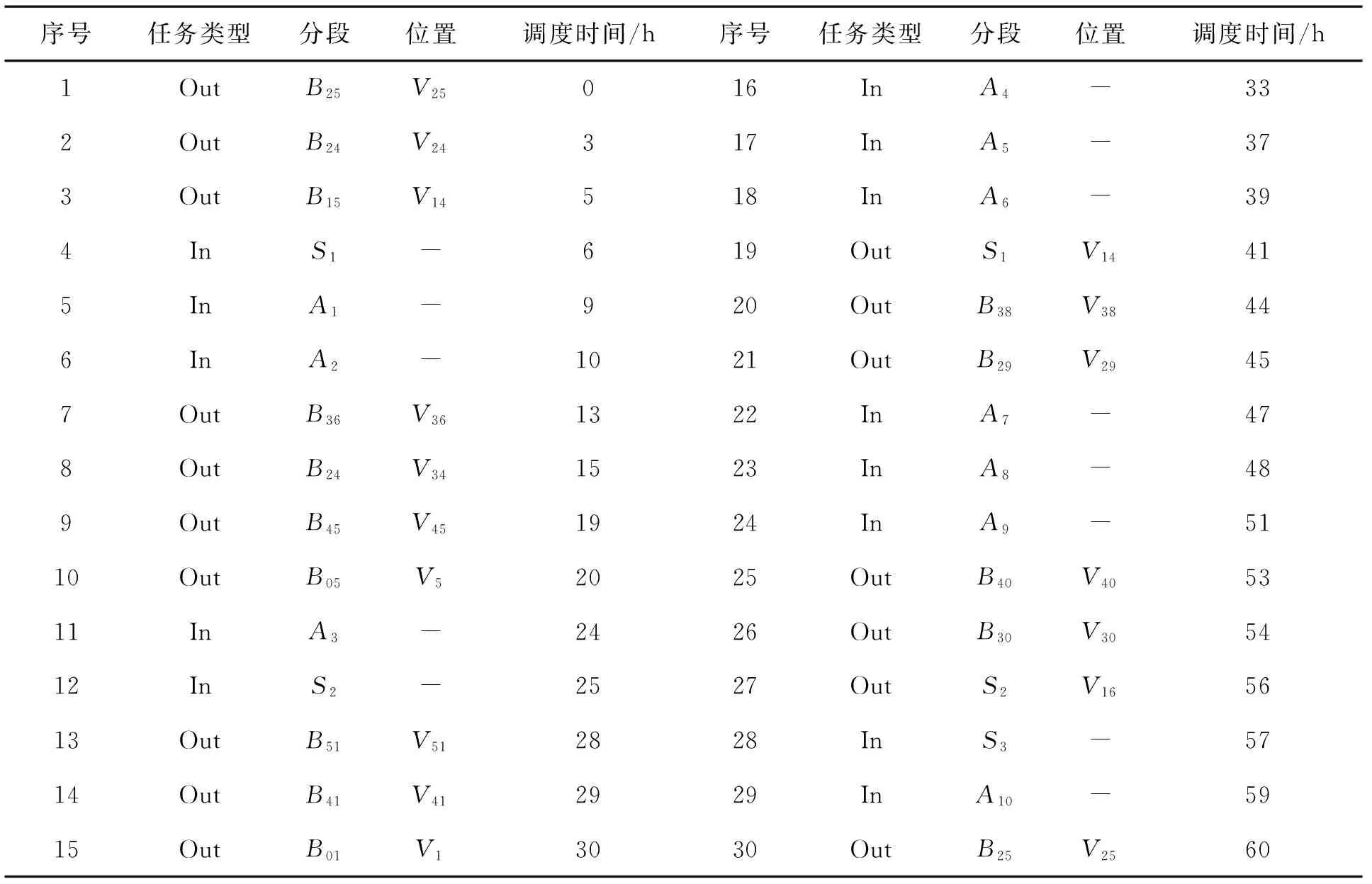
表1 堆場調度計劃

表2 堆場調度方案

4.2 數值分析

4.2.1 任務合并對減少臨時分段的影響

任務合并可以有效的減少調度過程中臨時分段的數量，而且任務允許任務合并的最大時間差δ和調度分段的數量都會影響最終的優化效果。為了比較不同參數下任務合并對減少臨時分段的影響，在δ為2、3、4、5 h，調度規模分別為60、80、100個分段的參數下共進行了12組試驗，其中各個分段的調度時間由[0,60 h]隨機生成。為了保證更好的試驗效果，對每組試驗進行5次，并取平均值。

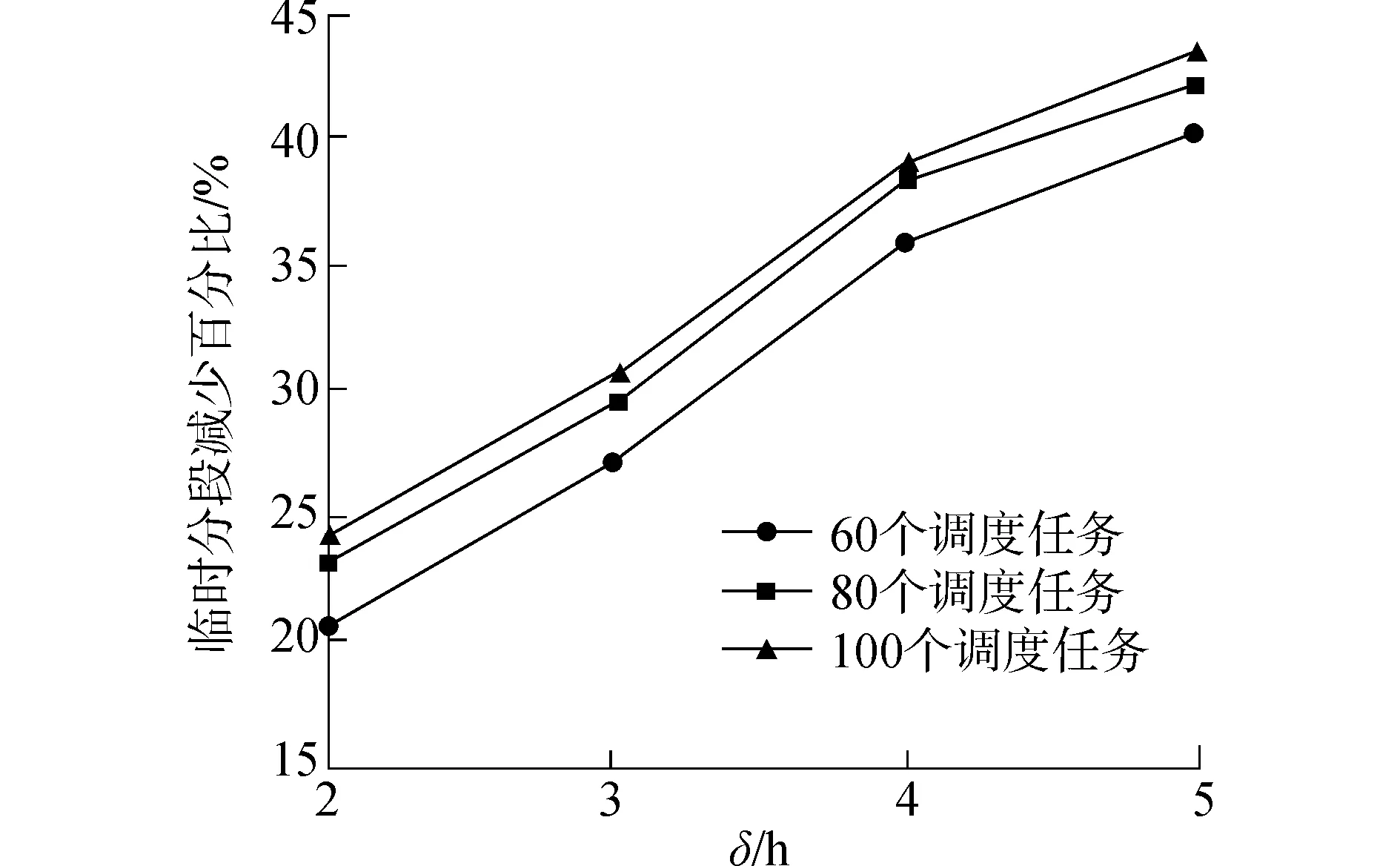
圖7 任務合并試驗結果Fig.7 Test results of task-merging

試驗結果如圖7所示，通過對堆場調度過程進行合理的任務合并，可以有效的減少調度過程中臨時分段的調度數量。隨著可接受任務合并時間差δ從2 h逐漸增加至5 h，臨時分段的減少百分比也相應的增加，而且相同的調度周期內，任務數量越多，任務合并的效果也約為明顯。但任務合并使一段時間內同時出場的分段數量增多，受后續工序的空間資源的制約，若δ值過大，例如δ=8 h時，一段時間內由于任務合并造成的同時出場分段的最大數量為5個，因此會引發場地堵塞等問題。

4.2.2 堆場存儲單元空置率e

在一定的調度周期內，堆場中一些存儲單元始終處于空置狀態，使得堆場的空間資源利用率不高，因此通過堆場存儲單元空置率可以反映出調度規則對堆場空間資源的利用情況，一個合理、高效的調度計劃會對堆場的存儲空間充分的利用。給出空置率的定義為

式中：Nume表示調度周期內堆場中始終沒有被用于存儲分段的存儲單元個數，M、N分別表示堆場的行數和列數。

為了比較不同調度規則和不同規模(40、50、60個分段)對存儲單元空置率影響，在堆場規格為6×10，初始負載率為65%的堆場中，分別運用不同的調度規則進行試驗，得到結果如圖8所示，可以看出制定的動態調度規則對于降低堆場空置率有一定的效果，且隨著調度規模的增加，效果更佳。雖然采用該調度規則空置率高于重新選位調度規則(位置隨機選擇)時的空置率，但是臨時分段采用重新選位的調度規則，會增加平板車的運輸距離，增加了調度計劃的復雜度。因此該調度規則對于降低堆場存儲單元空置率，提高堆場空間資源利用率有一定的效果。

臨時分段動態調度規則在不同堆場初始負載率時的調度效果也有所不同，因此試驗比較了不同初始負載率下(60%、70%、80%、90%)采用動態調度規則相比于移出暫存規則堆場空置率e的優化幅度。試驗的其他輸入參數為：1)調度規模：50個分段；2)M=6，N=10。

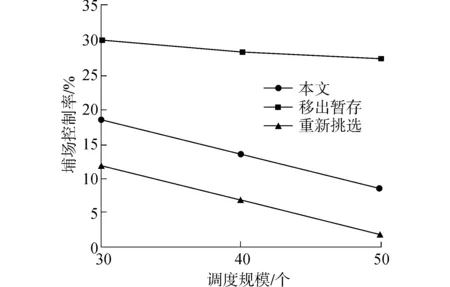
圖8 堆場空置率試驗結果Fig.8 Test results of Nume

對比結果如圖9所示，在堆場初始負載率較低時(60%、70%、80%)動態調度規則相比于將臨時分段移出堆場暫存待分段調度完成后移回堆場的調度方式對堆場存儲單元空置率的優化效果較為明顯。但堆場負載率較高時(90%)，本文的調度規則優化效果則不明顯，原因是該調度規則需要利用堆場中閑置的存儲單元，一旦堆場的負載率過高，堆場中空存儲單元數量也相應減少，這樣也就無法發揮動態調度的優勢。

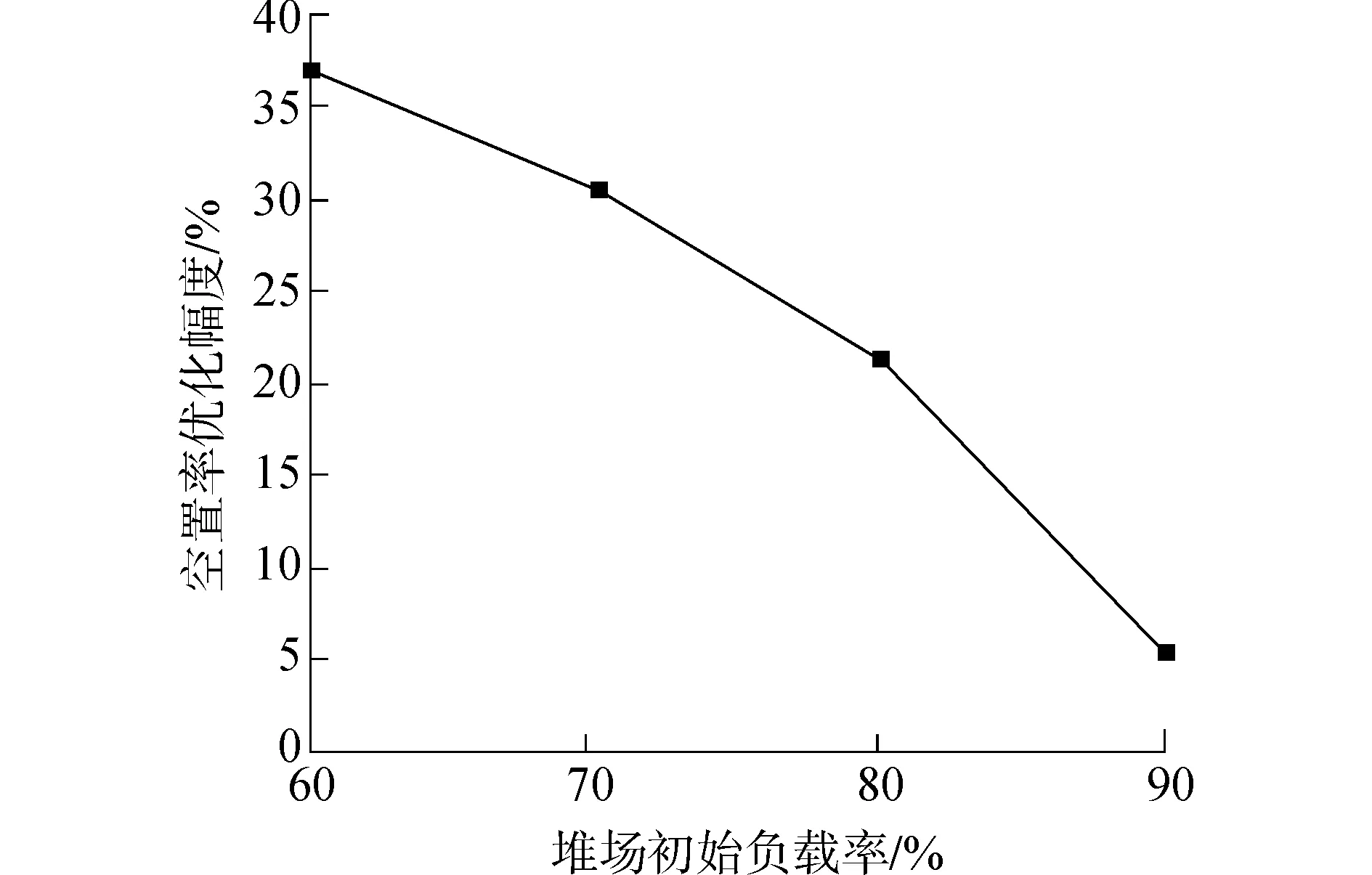
圖9 空置率優化幅度Fig.9 Optimization effect of Nume

4.2.3 調度規則對比

臨時分段的移動量是評價堆場調度方案優劣的標準，對于臨時分段的處理一般有：1)移出堆場暫存；2)重新選位。本文采用動態的調度規則，將臨時分段移動至相鄰的存儲單元進行存儲。如圖10所示，臨時分段的移動距離相比于其他調度規則有所下降，而且隨著調度分段數量的增加，該調度規則的優勢也更加的明顯。

圖10 不同調度規則對比Fig.10 Comparison of different scheduling rule

4 結論

本文通過對船舶分段堆場的調度過程進行研究，得出以下結論：

1)通過對堆場調度過程進行合理的任務合并，可以有效地減少調度過程中臨時分段的調度數量；

2)在較低的堆場初始負載率時本文的調度規則對堆場存儲單元空置率的優化效果較為明顯；

3)本文將臨時分段移動至相鄰的存儲單元進行存儲，在調度規模較大時，優勢更為明顯。

[1]PARK C, SEO J. Comparing heuristic algorithms of the planar storage location assignment problem[J]. Transportation research part E: logistics and transportation review, 2010, 46(1): 171-185.

[2]PARK C, SEO J. Mathematical modeling and solving procedure

of the planar storage location assignment problem[J]. Computers & industrial engineering, 2009, 57(3): 1062-1071.

[3]TAO Ningrong, JIANG Zuhua, QU Shipeng. Assembly block location and sequencing for flat transporters in a planar sto-rage yard of shipyards[J]. International journal of production research, 2013, 51(14): 4289-4301.

[4]張志英, 申鋼, 劉祥瑞. 基于最短路算法的船舶分段堆場調度[J]. 計算機集成制造系統, 2012, 18(9): 1982-1990.

ZHANG Zhiying, SHEN Gang, LIU Xiangrui. Block storage yard scheduling of shipbuilding based on shortest-path algorithm[J]. Computer integrated manufacturing systems, 2012, 18(9): 1982-1990.

[5]張志英, 徐建祥, 計峰. 基于遺傳算法的船舶分段堆場調度研究[J]. 上海交通大學學報, 2013, 47(7): 1036-1042.

ZHANG Zhiying, XU Jianxiang, JI Feng. Shipbuilding yard scheduling approach based on genetic algorithm[J]. Journal of Shanghai Jiao Tong University, 2013, 47(7): 1036-1042.

[6]陶寧蓉. 船舶分段建造過程中的資源調度優化研究[D]. 上海: 上海交通大學, 2013.

TAO Ningrong. Research on resouce scheduling problems during ship block assembly process[D]. Shanghai: Shanghai Jiaotong University, 2013.

[7]BAZZAZI M, SAFAEI N, JAVADIAN N. A genetic algorithm to solve the storage space allocation problem in a container terminal[J]. Computers & industrial engineering, 2009, 56(1): 44-52.

[8]PARK C, SEO J. Genetic algorithm of the planar storage location assignment problem[J]. Journal of the Korean institute of industrial engineers, 2009, 35(2): 129-140.

[9]ROH M I, CHA J H. A block transportation scheduling system considering a minimisation of travel distance without loading of and interference between multiple transporters[J]. International journal of production research, 2011, 49(11): 3231-3250.

[10]BANERJEE S K. Shipyard production systems design: a statistical approach[J]. International journal of production research, 1979, 17(6): 541-555.

Obstructive block stockyard scheduling and optimization based on heuristic rules

ZHANG Zhiying，ZENG Jianzhi

(School of Mechanical Engineering, Tongji University, Shanghai 201804, China)

The scheduling scheme of the obstructive blocks in the shipyard determined the efficiency and the cost of the stockyard scheduling operations. This paper took the scheduling process of the obstructive blocks as an optimization object. A mathematical model was established with the aim of minimizing the moving distance of the flat transporter. A dynamic scheduling rule for the obstructive blocks and the ultra-long blocks were proposed to make full use of the empty storage units, and which can ultimately obtain an optimal scheduling of the obstructive blocks. Meanwhile task-merging was used to optimize the sequence of the stockyard scheduling, thereby reducing the number of obstructive blocks during the scheduling process. Application data were acquired from a shipyard to validate the model and the scheduling rules, and the results showed that the proposed rules were effective to obtain a better stockyard scheduling scheme, and also improved the utilization of the space resource and scheduling efficiency.

stockyard; scheduling rules; ultra-long blocks; task-merging; heuristic rules

2015-08-06.

日期：2016-08-29.

國家自然科學基金項目(70872076)；上海市科技創新行動計劃項目(11dz1121803).

張志英(1971- )，男，副教授.

張志英，E-mail：zyzhang08@tongji.edu.cn.

10.11990/jheu.201508010

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160829.1421.032.html

O224；U673

A

1006-7043(2016)10-1416-08

張志英,曾建智. 基于啟發式規則的臨時分段調度計劃與優化[J]. 哈爾濱工程大學學報， 2016, 37(10): 1416-1423.

ZHANG Zhiying，ZENG Jianzhi. Obstructive block stockyard scheduling and optimization based on heuristic rules[J]. Journal of Harbin Engineering University, 2016, 37(10): 1416-1423.