基于遺傳算法的反例理解

李雅，黃少濱，李艷梅，遲榮華，郎大鵬

(哈爾濱工程大學 計算機科學與技術學院，黑龍江 哈爾濱 150001)

?

基于遺傳算法的反例理解

李雅，黃少濱，李艷梅，遲榮華，郎大鵬

(哈爾濱工程大學 計算機科學與技術學院，黑龍江 哈爾濱 150001)

在復雜系統的錯誤定位過程中，為了尋找合適的證例，提出一種結合模型檢測技術的基于遺傳算法的反例理解算法。利用遺傳算法，針對模型檢測中的模型具有初始狀態，狀態之間有相應的遷移關系等特點，初始化種群、設計適應度函數并進行指向性的變異操作。實驗表明該算法能快速有效的獲得最近證例，幫助模型檢測的反例理解。

模型檢測；遺傳算法；反例理解；錯誤定位

模型檢測[1]是一種驗證有限狀態并發系統(模型)是否滿足給定規約的方法[1-2]。當驗證的模型不滿足給定規約時給出反例是模型檢測的一個顯著特點。反例是證明模型違反給定規約的執行軌跡。調試者可以通過分析反例，理解錯誤產生的原因，對系統或模型進行修正。然而反例并沒有明確指出模型錯誤的原因，需要調試者根據自己的經驗定位錯誤，這需要花費大量的時間才有可能找到真正的錯誤，因此使用自動化的方法從反例中獲取有用的信息，幫助用戶定位錯誤，是目前的研究熱點。許多研究人員致力于研究錯誤定位的算法，提出了許多經典的算法，如基于路徑的語法級最弱前置條件的輔助算法[3]，利用克雷格插值的證明方法[4]，基于因果關系模型的方法[2,5]，基于可滿足性的方法[6-7]，以及基于證例和反例差異的方法[8-11]。本文的方法也是基于證反例的差異，證例是模型的一種遷移路徑，并且滿足待驗證規約。為了獲得與反例最接近的證例，本文提出了一種利用遺傳算法獲取證例的方法。遺傳算法 (genetic algorithm, GA)是1975年由John Holland[12]教授提出，在許多研究領域都得以應用，例如自動控制、數據挖掘[13]、機器學習、組合優化[14]等。在軟件方面主要用于測試用例的自動生成和優化選擇，它從代表問題可能潛在解集的一個種群開始，通過選擇、交叉和變異等操作，使種群逐漸集中于搜索空間中越來越好的區域。演化的代數主要取決于代表問題解的收斂狀態，末代種群中的最佳個體作為問題的最優近似解。因此本文構建一種基于遺傳算法的，具有普適性的求解最近證例的方法。該方法用Kripke結構來刻畫系統行為，用線性時態邏輯LTL描述需要驗證的規約，針對模型檢測中模型的特點初始證例種群，使用兩個適應函數對應的最佳個體進行交叉操作，具有指向性的變異操作，最終獲得末代種群中的最佳個體，即最近證例。相對于其他的獲取證例的方法，本文在證例搜索的過程中引入啟發式信息，提高系統狀態空間搜索的效率，并且由于遺傳算法不依賴于具體問題而直接進行搜索，所以本文的方法適用性更強，應用范圍更廣。

1 模型檢測與GA的基本理論

1.1 模型檢測相關定義

模型檢測中通常使用狀態遷移圖來描述系統模型，Kripke結構是一種常用的狀態遷移圖。本文的待驗證模型以Kripke結構表示，首先給出Kripke結構的定義。

令V={v1,v2,…,vn}是一個有限布爾變量集，Dv1,Dv2,…,Dvn分別為v1,v2,…,vn的數據域，定義在V上的Kripke結構為：

定義1 Kripke結構是一個四元組K=(S,I,T,L)其中：S?Dv1,Dv2,…,Dvn是有限狀態集合，I?S是初始狀態集，T?S×S是狀態遷移關系，標記函數L:S→2v標記在狀態S真變量的集合。

定義2 定義在Kripke結構K上的路徑π是一個狀態序列π=s0,s1,s2…，其中s0∈I，si∈S , i∈N, π(i)=si;πi=si,si+1,si+2…。Path(K)表示K中所有路徑的集合。

定義3 線性時態邏輯LTL在每一個時刻，只有一個可能的次態，LTL公式的語法定義如下：

φ::= ⊥| ┬ |p| (φ) | (φ∧φ) | (φ∨φ) | (φ→φ) | (Xφ) | (Fφ) |(Gφ) | (φUφ) | (φWφ) | (φRφ)

其中p是取自某原子集的任意命題原子。X、F、G、U、W和R為時態連接詞。分別表示為“下一個狀態”(neXt)，“某未來狀態”(Future)，“所有未來狀態”(Globally)，“直到”(Until)，“弱-直到”(Weak-until)和“釋放”(Release)。

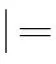
1) π|=p?p∈L(s0)

3) π|=φ1∧φ2?π|=φ1且π|=φ2

4) π|=φ1∨φ2?π|=φ1或π|=φ2

5) π|=φ1→φ2?只要π|=φ1就有π|=φ2

6) π|=Xφ?π2|=φ

7) π|=Gφ ? ?i≥1, πi|=φ

8) π|=Fφ ? ?i≥1, πi|=φ

9) π|=φUφ ? ?i≥1, 使得πi|=φ并且?j=1,2,…,i-1，有πj|=φ

10) π|=φWφ ? ?i≥1，使得πi|=φ并且?j=1,2,…,i-1，有πj|=φ或者?k≥1 ，有πk|=φ

11) π|=φRφ?或者?i≥0，使得πi|=φ，并且?j=1,2,…,i，有πj|=φ；或者?k≥1，有πk|=φ

Biere等提出的有界模型檢測(bounded model checking,BMC)不同于傳統的符號模型檢測[15]，它在有限長度k(稱其為限界)的范圍內查找反例。如果在限界k內沒有發現反例，則增加k的值直至問題變得難解，或者達到預先設定的上界。

根據LTL語義，BMC問題可以規約為命題可滿足問題，若M為Kripke結構的待驗證模型，f為BMC要驗證規約的否定形式的公式，k為界限，第i個和第i+1個周期的狀態為Si和Si+1，狀態轉換關系為Ti(Si,Si+1)，則BMC轉換公式可以表示為：[[M,f]]k。

定義5 (BMC轉換公式) 設M為Kripke結構，f為待驗證的LTL規約說明否定形式的NNF公式，k為整數，則BMC轉換公式為

(1)

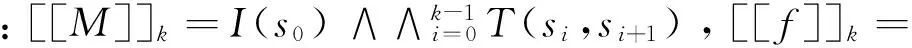
在有界模型檢測方法中，將式(1)轉換為CNF格式的SAT問題，并用SAT求解器求解，即可驗證模型是否滿足給定規約。在界限k內，反例的長度為k，基于界限模型檢測的路徑和反例定義如下：

定義6 反例 在Kripke結構K上，對LTL公式f和界限k，若有π|=kf，則稱π為f的反例。

定義7 證例 在Kripke結構K上，對LTL公式f和界限k，若有π|=kf，且π∈Path(K)，則稱π為f的證例。

1.2 反事實依賴

D.Lewis[16]提出的基于反事實的原因定義為通過搜索與反例最近證例定位錯誤的方法提供了邏輯基礎。Lewis認為不同源自于“cause”，如果原因c不發生則所產生的影響e也不會發生，并將原因的定義建立在反事實依賴的基礎之上。其中反事實依賴的定義為：

定義8 反事實依賴 設在世界w中有命題e和c，則反事實ce為真，當且僅當

1)世界w中，命題e和c同時為真；(即：c(w)∧e(w))；

2)存在世界w’，有c(w′)∧e(w′)∧

定義9 (原因) 設在世界w中，命題c和e同時為真。則在w中c是e的原因，當且僅當在世界w′中，ce。

定理1 設f是待驗證規約，t是反例，w是離t最近的證例，c是t中與w中取值不同的變量的集合，則c是f的原因。

證明：根據假設有，在w中有c(w)∧f(w)。假設存在某條與w不同的路徑w′，有c(w′)∧f(w′)，并且d(t,w′)≤d(t,w)。則w′中存在一些其他的與w不同的變量v?D，那么這些變量v在t中的取值必然與w′中的不同。于是d(t,w′)>d(t,w)，矛盾，因此w′不存在。在t中有cf，c是f的原因。

1.3 遺傳算法

遺傳算法(GA)是模仿自然界生物遺傳進化過程中的“物競天擇、適者生存”的思想，是一種全局尋優搜索算法，它首先對問題的可行解進行編碼，組成染色體，然后通過模擬自然界的進化過程，對初始種群中的染色體進行選擇、交叉和變異，通過一代代進化來找出最優適應值的染色體來解決問題。遺傳算法具有很強的全局搜索能力和較強的自適應性，適合解決連續變量函數優化問題和離散變量的優化組合問題。

遺傳算法計算簡單，具有超高的全局搜索能力[17]。在模型檢測中，模型以Kripke結構給出并具有初始狀態，在設計遺傳算法的初始種群時，每個個體的第一個基因片段必須是模型的初始狀態，因此初始種群的個體數相對較小，算法比較容易達到收斂狀態。

定義8給出了最近證例需要滿足的條件，不僅需要滿足待驗證規約還應該與反例的距離最近，給遺傳算法應用于反例理解提供了適當的適應度函數。因此遺傳算法適用于模型檢測的中的證例搜索。

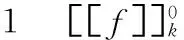
表和的遞歸定義

2 基于遺傳算法的證例生成

本節討論利用遺傳算法來生成與反例最近的證例的算法。反例是當模型不滿足待驗證規約時生成的一條狀態的序列。證例同樣是模型中的一條狀態遷移路徑，但是它不違反待驗證規約。最近證例就是離反例最近的證例。本文利用遺傳算法，將最近距離和對于待驗證規約的可滿足度作為檢測最近證例的適應度，而最終求得最近證例，幫助自動的定位錯位。

2.1 編碼

遺傳算法中首要問題就是編碼問題，也是設計遺傳算法時的一個關鍵步驟。常見的編碼方法有字符串表示法和鄰接基因位編碼法。本文采用的是字符串編碼方法。按照路徑上狀態的順序進行編碼，具體實現方式是：按照路徑上狀態的出現順序，以及標簽變量的值進行編碼。以圖1的Kripke結構為例，有限長度路徑π=(s0,s1,s2)，L(s0)={p,q}，L(s1)={q,r}和L(s2)={r}。若狀態s0編碼為110，s1編碼為011，s2為001。則路徑π的編碼為110011001。

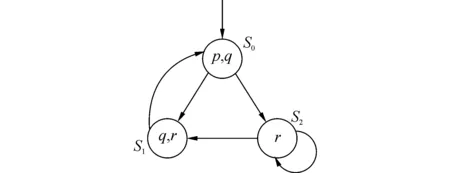
圖1 一個簡單的Kripke結構Fig.1 A simple Kripke structure

2.2 初始種群生成

在遺傳算法的初始種群中，如果每個個體都具備一定的精度且個體間多樣性較強時，則可以提高算法搜索效率，加速算法收斂。在模型檢測中，模型被表示成一個Kripke結構，而所求的證例具有特定起始點，也就是從初始狀態集的某一個起始狀態出發的系統運行路徑。因此與隨機生成初始群體的方法不同, 本文生成初始種群的方法是基于特定起始點的，試圖能夠快速產生具有一定精度和較強多樣性的初始種群。如定義2所示，系統的運行路徑是一個狀態的無限序列：

本文中模型的驗證使用的是有界模型檢測，反例的長度為k，需要考慮路徑上是否存在循環。路徑可以表示為

式中：u和v是有限長度的狀態序列，u=s0,s1……,si-1，v=si,si+1……,sk,i

給定長度k(k≥1)，考察從初始狀態集I單步可達的所有狀態的集合S1。依次考察S1中的每一個狀態s1，若從s1出發，不存在遷移，則這一狀態為死鎖狀態；若存在不止一條的遷移，則隨機選取一條遷移執行，獲得路徑中的下一個狀態。重復以上過程，直至得到第k個狀態。

如果考察的模型含有n(n∈N+)個初始狀態，從每個初始狀態出發的遷移數分別是：x0,x1……,xn，則初始種群的大小為：x0+x1+……+xn。

2.3 適應度

為了體現染色體的適應能力，引入了對問題中的每一個染色體都能進行度量的函數，叫適應度函數。通過適應度函數來決定染色體的優、劣程度，它體現了自然進化中的優勝劣汰原則，它是評價新解優劣的唯一標準。

一般而言，適應度函數是直接由目標函數變換而成的，有時也要根據問題的要求，對目標函數進行一定的適應度尺度變換。模型檢測中的證例，需要是模型中的路徑，并且要滿足待驗證規約。與此同時要求解與反例最近的證例，證例w與反例t的距離d(w,t)越短越好，因此需要將種群中的個體對于待驗證規約的滿足度s和d(w,t)共同作為遺傳算法的適應度函數。

本文基于有界模型檢測，按照定義5和表1可以得到待驗證規約的CNF形式的公式[[f]]k，滿足度s即基于式子[[f]]k。例如布爾公式：

(2)

如圖1的路徑π=s0,s1,s2={x1=1,x2=1,x3=0,x4=0,x5=1,x6=1,x7=0,x8=0,x9=1}滿足布爾公式(2)中的8個子句，不滿足子句x3∨x6∨x7∨x9，因此s=8。

本文中的個體編碼采用的是字符串編碼方式，因此d(w,t)采用字符串的編輯距離來度量[18]，值得注意的是路徑上的每個狀態記為一個字符。由于反例中也包含了許多值得遺傳給后代的有益信息，在生成初始種群時并沒有將反例排除在外，并且一般情況下適應度越高越好，因此在本算法中使用d(w,t)+1的倒數，可使求倒數不出現錯誤。

定義10 對于給定的規模為n的群體P={π1,π2,…,πn}，t為反例，個體πi∈P(i=1,2,…,n)的適應值為F(πi)，適應度函數為一維二元向量:

(3)

2.4 遺傳操作

簡單遺傳算法的遺傳操作主要有三種:選擇(selection)、雜交(crossover)和變異(mutation)。改進的遺傳算法大量擴充了遺傳操作，以達到更高的效率。

2.4.1 具有多評價指標的選擇操作

遺傳算法中的選擇操作就是用來確定如何從父代種群中按某種方法選取哪些個體遺傳到下一代種群中的一種遺傳運算。選擇操作建立在對個體的適應度進行評價的基礎上。使用選擇算子(也叫復制算子reproduction operator)來對種群中的個體進行優勝劣汰操作：適應度較高的個體被遺傳到下一代的概率較大；適應度較低的個體被遺傳到下一代的概率較小。

2.4.2 交叉

在選擇算子的作用下，得到了新一代的個體，但是這些個體都是從上一代存活下來的，本質上還是上一代的個體，因此這些個體之間必須經過相互之間的交叉以產生新的個體，通過相互交換優秀的基因，使得整個種群向更優的方向進化。遺傳算法中的交叉算子對算法進行全局搜索方面起到了重要的作用。本文采用的是一種通用的算子：“常規交叉法”。該交叉算子的使用非常的直觀和簡單。

首先是選擇兩個父代進行交叉，選擇的方式是根據個體的適應度來決定的。然后產生一個區間[1，N]的隨機數k作為交叉位。基于本文的編碼，在選擇交叉位時將一個狀態作為一個完整的基因片段。也就是說，如圖2所示N=3，當選定的隨機數k=2時交換的位置實際是個體編碼的位置6(變異和修正的位置計算與此相同)。最后就是產生子代1和子代2，子代1交叉位之前的基因來自父代1交叉位之前的基因，而交叉位之后的基因則從父代2中按順序選取那些沒有出現過的基因，以補充完整整個解。子代2也是進行相似的處理。圖3給出了這種交叉法的一個例子。

圖2 交叉操作Fig.2 Crossover operation

在完成交叉操作之后，常規的交叉方法容易產生非法的解，因此要對解進行修正。如圖2中子代1存在兩個011(圖1中的s1)狀態，為了最大的保持父代和新產生的基因片段，在原父代中刪除交換來的基因片段中含有的狀態，最終去除了重復狀態的父代基因加上交叉來的基因完成了基因的修復。這樣做既保留了父代基因也添加了交叉來的基因，對原基因和新基因進行了保持。例如圖2交叉后的子代1，進行的子代修正操作如圖3所示。

圖3 子代基因修正Fig.3 Gene correction

2.4.3 變異

從遺傳算法的觀點來看，解的進化主要靠選擇機制和交叉策略來完成，變異只是為選擇、交叉過程中可能丟失的某些遺傳基因進行修復和補充，變異在遺傳算法的全局意義上只是一個背景操作。變異操作產生新的搜索點，擴大搜索空間，避免算法過早收斂到局部最優解，起著提高種群多樣性和搜索算子的雙重作用。

在使用遺傳算法進行證例發現時，交叉操作導致新一代種群生成許多無效的路徑。鑒于此，本文提出了具有修正功能的定向變異策略。

具體的定向變異策略具體過程如下：

1)對每個個體，考察其是否屬于Path(K)。

2)如果存在不屬于Path(K)，找到所有的錯誤遷移的起始狀態，并計算其單步可達狀態集合。從中隨機選擇一個狀態作為變異后的狀態。

2.5 算法描述

輸入：K，f，T/*K表示Kripke結構的模型，f為待驗證規約，T為算法的最大迭代次數*/

輸出：w，F(w) /*w表示最優證例，F(w)為w的適應值 */

開始

1)按照基于特定起始點的方法得到初始種群Y。

2)計算種群Y中個體的適應度，并獲得最大適應度向量Fmax。

3)如果為達到預定最大迭代次數，依據選擇策略，對選出的個體進行交叉，并且修正新一代個體。

4)進行具有指向性的變異操作。

5)產生新一代種群Y，計算適應度，獲得最大適應度向量Ftemp。

6)如果Ftemp優于Fmax則將Ftemp賦給Fmax，返回3)，如果Ftemp次于Fmax，則結束循環。

7)從種群中選擇所需的最優個體。

結束

3 算法分析與實驗結果

3.1 正確性與可終止性

基于遺傳的證例搜索算法是可終止的，算法有兩種結束方式：1)執行的每一代操作都有一個最大的適應度值，若經過遺傳操作交叉和變異之后產生的新一代的最大適應度值比其父代的最大值沒有增大；2)算法執行完預定的最大迭代次數[19]。因此計算過程最多在T次迭代后結束，T為預先設定的最大迭代次數，即本文的算法滿足可終止性。遺傳算法的適應度函數保證了所求解最優，選擇操作的修正和定向的變異保證所求解是模型中的路徑，這也就保證了本文算法滿足正確性。

3.2 時間復雜度分析

探討基于遺傳算法的證例生成算法的時間復雜度，首先要確定模型的狀態數n，遷移數為t，初始狀態的遷移數x0,x1…,xm，則種群規模L=x0,x1…,xm，k為路徑的最大長度，則初始化種群的時間復雜度為O(Lk)。對種群進行交叉操作的時間復雜度為O(Lk/2)。變異操作中判斷一個個體是否是正確路徑的時間復雜度為O(kt)，計算單步可達狀態集合的時間復雜度為O(t)。而對種群進行適應度計算的時間復雜度為O(Lk)。

通過上述分析可知，基于遺傳算法的證例生成算法的最大時間復雜度為O(kt)，k表示最大路徑長度是一個常數。

3.3 實驗結果

為了驗證本文的算法，實現了一個java語言的編寫的遺傳算法的證例生成程序。程序運行環境為雙核Intel Core i5-4210U @ 1.70 GHz 2.40 GHz處理器，內存為4 GB，操作系統為64位的Windows 7。

表2 實驗分析結果

從表2中數據可以看出，Mutex2模型驗證是生成反例最長，算法生成的最優解與反例相差為1，算法的分值最高需要的人工操作也最少。相反AFS-1與Policy模型的φ1規約的分值為0，是由于反例的長度為2，最優解與反例的距離為2，也就是反例上所有的狀態都被認為是錯誤的，這就需要更多的人工操作來判斷結果是否正確。表2中GN表明算法能在極少的進化步驟內就能找到最優解，本文算法很快能達到收斂狀態，效率很高。

4 結論

本文將遺傳算法引入模型檢測中的反例理解，提出了一種利用遺傳算法，獲取最近證例的算法，充分的利用了反例中的信息和模型的特點，得出如下結論：

1)使用遺傳算法可以快速準確的找到反例的最近證例，對于復雜度很高的模型有很好的魯棒性；

2)使用多個評價指標和定向的變異策略，不僅能在極少的進化次數內找到最優解，并且具有很好的收斂性，使得算法的時間復雜度顯著降低。

由于遺傳算法具有良好的并行性，本文提出的算法可以擴展為相應的并行搜索算法，以加快求解速度。

[1]CLARKE E, GRUMBERG O. Model checking[M]. Cambridge: MIT Press, 1999.

[2]BEER I, BEN-DAVID S, CHOCKLER H, et al. Explaining counterexamples using causality[J]. Formal methods in system design, 2012, 40(1): 20-40.

[3]WANG Chao, YANG Zijiang, IVANIF, et al. Whodunit? Causal analysis for counterexamples[M]//GRAF S, ZHANG Wenhui. Automated technology for verification and analysis. Berlin Heidelberg: Springer, 2006: 82-95.

[4]黃宏濤, 黃少濱, 陳志遠, 等. 基于克雷格插值的反例理解方法[J]. 吉林大學學報: 理學版, 2013, 51(1): 94-100.

HUANG Hongtao, HUANG Shaobin, CHEN Zhiyuan, et al. Understanding counterexamples based on Craig interpolation[J]. Journal of Jilin university: science edition, 2013, 51(1): 94-100.

[5]HALPERN J Y, PEARL J. Causes and explanations: a structural-model approach. Part I: Causes[J]. British journal for the philosophy of science, 2005, 56(4): 843-887.

[6]SüLFLOW A, FEY G, BLOEM R, et al. Using unsatisfiable cores to debug multiple design errors[C]//Proceedings of the 18th ACM Great Lakes symposium on VLSI. New York, 2008: 77-82.

[7]CHEN Yibin, SAFARPOUR S, MARQUES-SILVA J, et al. Automated design debugging with maximum satisfiability[J]. IEEE Transactions on computer-aided design of integrated circuits and systems, 2010, 29(11): 1804-1817.

[8]GROCE A, VISSER W. What went wrong: explaining coun-terexamples[M]//BALL T, RAJAMANI S K. Model Checking Software. Berlin Heidelberg: Springer, 2003, 2648: 121-136.

[9]GROCE A, CHAKI S, KROENING D, et al. Error explanation with distance metrics[J]. International journal on software tools for technology transfer, 2006, 8(3): 229-247.

[10]CHAKI S, GROCE A, STRICHMAN O. Explaining abstract counterexamples[C]//Proceedings of the 12th International Symposium on Foundations of Software Engineering. Newport Beach, 2004: 73-82.

[11]WANG Tao, ROYCHOUDHURY A. Automated path generation for software fault localization[C]//. Proceedings of the 20th IEEE/ACM International Conference on Automated Software Engineering. New York, 2005: 347-351.

[12]HOLLAND J H. Adaptation in Natural and Artificial Systems[M]. Cambridge: MIT Press, 1992.

[13]陳國彬, 張廣泉. 基于改進遺傳算法的快速自動組卷算法研究[J]. 計算機應用研究, 2015, 32(10): 2996-2998.

CHEN Guobin, ZHANG Guangquan. New algorithm for intelligent test paper composition based on improved genetic algorithm[J]. Application research of computers, 2015, 32(10): 2996-2998.

[14]曲志堅, 張先偉, 曹雁鋒, 等. 基于自適應機制的遺傳算法研究[J]. 計算機應用研究, 2015, 32(11): 3222-3225.

QU Zhijian, ZHANG Xianwei, CAO Yanfeng, et al. Research on genetic algorithm based on adaptive mechanism[J]. Application research of computers, 2015, 32(11): 3222-3225.

[15]BIERE A, CIMATTI A, CLARKE E M, et al. Bounded model checking[J]. Advances in computers, 2003, 58: 117-148.

[16]LEWIS D. Causation[J]. The journal of philosophy, 1973, 70(17): 556-567.

[17]施小純. 基于反例搜索的啟發式模型檢測算法的研究[D]. 北京: 中國科學院研究生院(軟件研究所), 2004: 49-50.

SHI Xiaochun. A heuristic algorithm for model-checking based on counter example finding[D]. Beijing: Institute of Software Chinese Academy of Sciences, 2004: 49-50.

[18]HUTH M, RYAN M. Logic in Computer Science: Modeling and Reasoning about Systems[M]. London: Cambridge University Press, 2004.

[29]張健沛, 李泓波, 楊靜, 等. 基于歸屬不確定性的變規模網絡重疊社區識別[J]. 電子學報, 2012, 40(12): 2512-2518.

ZHANG Jianpei, LI Hongbo, YANG Jing, et al. Variable scale network overlapping community identification based on identity uncertainty[J]. Acta electronica sinica, 2012, 40(12): 2512-2518.

[20]LEUE S, BEFROUEI M T. Counterexample explanation by anomaly detection[M]//DONALDSON A, PARKER D. Model Checking Software. Berlin Heidelberg: Springer , 2012: 24-42.

[21]WING J M, VAZIRI-FARAHANI M. A case study in model checking software systems[J]. Science of computer programming, 1997, 28(2/3): 273-299.

An algorithm for explanation counterexamples by use of a genetic algorithm

LI Ya，HUANG Shaobin，LI Yanmei，CHI Ronghua，LANG Dapeng

(College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China)

In order to seek the appropriate witness to help fault location of a complex system, a counterexample understanding algorithm in combination with a model checking technique on the basis of a genetic algorithm was proposed. The model used for model checking has an initial state, and the transfer relationship exists between the corresponding states. Therefore, a population was initialized. Also, a fitness function was designed and a directive mutation operation was conducted. Experimental results demonstrate that the algorithm can find the nearest witness rapidly and effectively and help the counterexample understanding of model checking.

formal method; model checking; genetic algorithm; explanationing counterexample; fault localization

2015-09-01.

日期：2016-08-29.

國家科技支撐計劃課題(2012BAH08B00).

李雅(1985-), 女, 博士研究生；

黃少濱(1965-), 男, 教授,博士生導師.

李雅，E-mail:liya_heu@163.com.

10.11990/jheu.201509006

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160829.1421.048.html

TP311.5

A

1006-7043(2016)10-1394-07

李雅，黃少濱，李艷梅，等. 基于遺傳算法的反例理解[J]. 哈爾濱工程大學學報， 2016, 37(10): 1394-1399.

LI Ya，HUANG Shaobin，LI Yanmei， et al. An algorithm for explanation counterexamples by use of a genetic algorithm[J]. Journal of Harbin Engineering University, 2016, 37(10): 1394-1399.