基于無源性的無刷直流電動機速度控制

譚傳接，楊向宇，趙世偉

(華南理工大學，廣州 510640)

?

基于無源性的無刷直流電動機速度控制

譚傳接，楊向宇，趙世偉

(華南理工大學，廣州 510640)

采用一種基于無源性控制算法對無刷直流電動機進行速度控制。利用電機的電壓方程、電磁轉矩方程和運動方程，推導出基于電機狀態誤差變量的能量函數，并針對實際運行過程中電機存在負載擾動問題，引入負載擾動觀測器，通過設計合適的控制律，使得電機狀態誤差變量的能量函數能收斂于期望值。仿真與實驗結果表明，該控制算法對無刷直流電動機速度控制具有控制簡單、魯棒性較好和穩態性能良好等優點。

無刷直流電動機；無源性控制；速度控制；負載觀測器

0 引 言

無刷直流電動機(以下簡稱BLDCM)是從傳統的有刷直流電動機發展而來的。它既保留了直流電機的機械特性，又通過安裝電子換相裝置取代直流電機的電刷和換向器，解決了直流電機換相火花的問題，提高了電機運行可靠性。BLDCM具有本體結構簡單、體積小、功率密度大、噪聲小、運行可靠等一系列優點，適用于航空航天、電動車、電腦外設和家用電器等領域[1]。

BLDCM是一個多變量、非線性的控制系統，采用傳統的PID調節器雖然能達到較好的控制效果，但PID調節器對電機運行工況適應性差，控制效果難以保證[2]。文獻[3]采用模糊遺傳算法優化對BLDCM進行控制，雖然系統很好地對預設速度參考模型的跟蹤，具有較好的魯棒性，但算法比較復雜。無源性控制是一種非線性控制方法，它通過尋找與被控對象狀態相關的能量函數，設計無源性控制律，使得系統狀態變量能漸進收斂至期望值，從而達到控制的目的[4]。文獻[5-7]分別研究了無源性控制算法在直線開關磁阻電機、鼠籠式感應電機和無刷雙饋電機的應用，控制算法具有全局穩定性，實現了電機的轉速控制。

本文在分析BLDCM數學模型的基礎上，將無源性控制算法應用于BLDCM速度控制系統，并通過設計負載觀測器來抑制電機負載擾動對電機速度的影響，以提高系統的速度控制效果與魯棒性。最后在MATLAB/Simulink環境進行BLDCM速度控制系統仿真，并通過實驗驗證無源性控制算法對電機速度的控制效果。

1 BLDCM數學模型

為得到BLDCM的電壓方程，電磁轉矩方程和運動方程。根據BLDCM的結構原理，進行以下假設：電機具有三相完全對稱，空間上互差120°的定子繞組；電機具有梯形波的三相繞組反電動勢；電機三相繞組的電感、電阻參數一致；電機具有均勻的氣隙磁導，磁路不飽和 。

BLDCM的電壓方程可表示：

(1)

式中:ua,ub,uc為電機的對參考地電壓；ia,ib,ic為電機的相電流；Ra,Rb,Rc為相電阻；Laa,Lbb,Lcc為相自感；Lab,Lac,Lba,Lbc,Lca,Lcb為相互感；ea,eb,ec為相電動勢；un為電機三相繞組中點對參考地電壓；p為微分算子。

由于電機定子繞組采用三相星形接法，并采用兩兩導通的控制方式，則有ia+ib+ic=0，由電機建模的假設條件，有Ra=Rb=Rc=R，Laa=Lbb=Lcc=L1，Lab=Lac=Lba=Lbc=Lca=Lcb=M，記電機三相繞組中點電壓為參考地電壓，反電動勢大小為e，正常換相導通時，有:

(2)

式中:Cj(j=a，b，c)為電機相反電動勢系數。將式(2)代入式(1)可得電壓方程：

(3)

式中:L為等效相電感，L=L1-M。

BLDCM的等效電路圖如圖1所示。

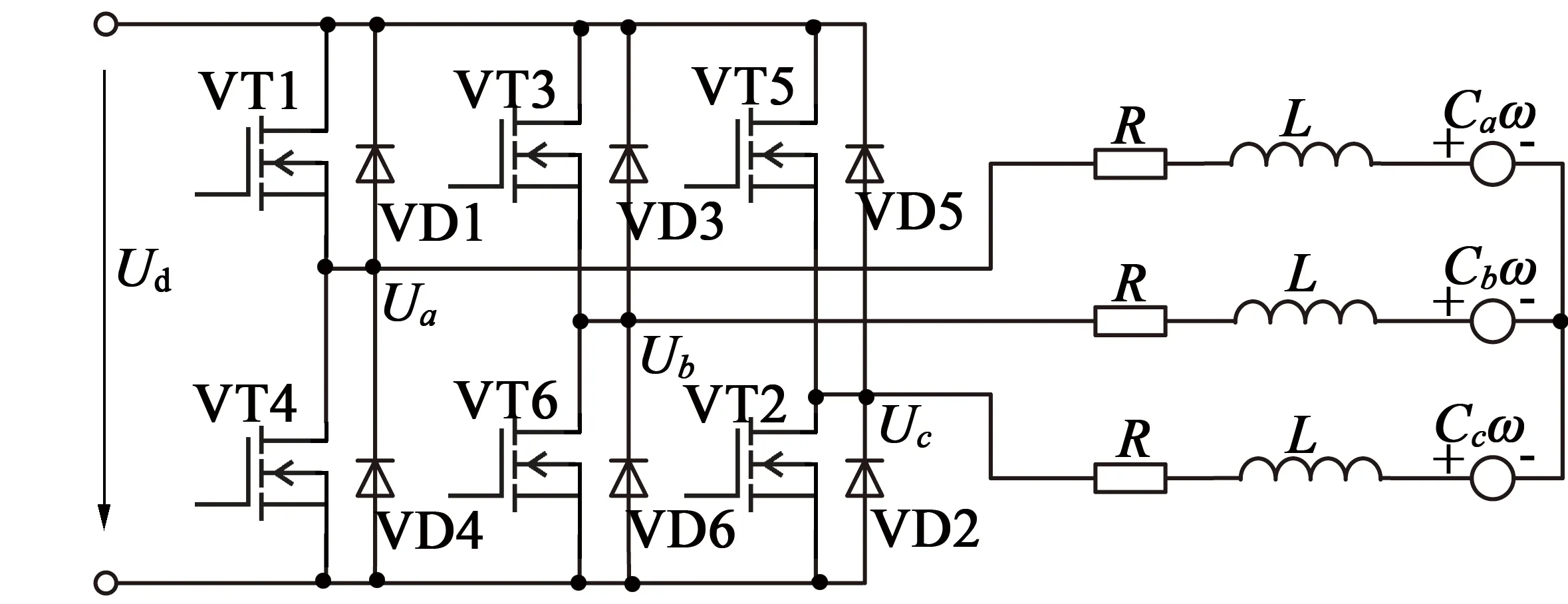
圖1 BLDCM的等效電路

BLDCM的電磁轉矩方程：

(4)

式中:Te為電機的電磁轉矩。

將式(2)代入式(4)可得電機轉矩方程如下：

(5)

BLDCM的運動方程：

(6)

式中:B為摩擦系數;J為電機的轉動慣量;ω為電機角速度;TL為負載轉矩。

2 無源性控制器設計

選擇BLDCM的三相電流和角速度作為狀態變量，則電機狀態變量表示為XT=[iaibicω]，結合式(3)、式(5)、式(6)，可得電機狀態方程：

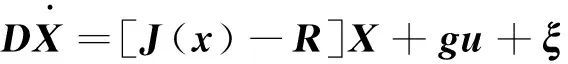
(7)

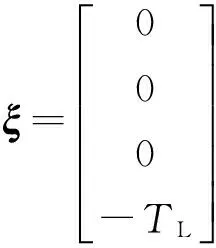
定義狀態誤差向量為E=X-Xd，其中Xd為系統狀態變量參考值。將狀態誤差代入式(7)中，可以得到電機狀態變量誤差方程：

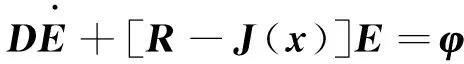
(8)

其中:

(9)

取電機狀態誤差的能量函數:

(10)

狀態變量誤差函數對時間的導數可以表示為下式：

(11)

由式(8)和式(11)可得：

(12)

由于J(x)是一個反對稱矩陣，所以ETJ(x)E=0；由式(12)可表示：

(13)

根據Lyapunov穩定性判別定理，如果可以保證H(·)(E)在其平衡點處取得零值和在狀態域的其他點上具有負值，那么狀態誤差函數H(E)將會耗散到零，而狀態變量將趨近期望值。通過設定合適的控制律，使等式(14)成立:

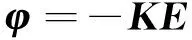
(14)

其中，K=diag(k1,k2,k3,k4)，K為正定的四階對角矩陣，代入式(13)可得：

(15)

由式(9)和式(14)可以得到：

(16)

式(16)就是控制器所要求解的控制律。它具有全局穩定性，在負載擾動已知的情況下，能保證系統狀態變量達到期望值。

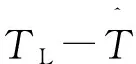
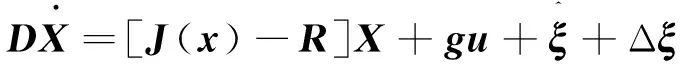
(17)

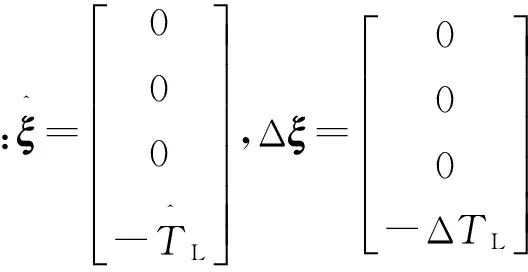
ξ(＾)為系統觀測到的擾動向量，Δξ為系統實際擾動與觀測擾動之差。

其誤差狀態方程可表示如下：

(18)

記:

(19)

將其代入式(18)可得：

(20)

那么構造關于負載擾動未知的系統狀態誤差能量函數如下：

(21)

式中：k為一個正數。

此時系統狀態誤差函數對時間的導數表示：

(22)

為保證在電機參數攝動和負載擾動下保持穩定，可以將控制器設計:

(23)

(24)

將狀態誤差向量E和擾動偏差向量Δξ代入式(24)可得:

(25)

(26)

為計算方便，對控制參數進行簡化，可以記k1=k2=k3=ki，k4=kw，結合式(19)，式(23)，式(26)可得：

(27)

由于電機采用兩兩導通方式，電機處于兩相導通，第三相懸空的狀態，導通兩相電流大小相等，方向相反，懸空相電流為零，所以只需要觀測到電機的速度和導通相的電流就可以對電機進行控制。

此時，記電機電流參考值為id，實際電流大小為i，那么導通的兩相電流參考值電流應取id與-id，實際電流為i和-i，相反電勢系數分別為Ce和-Ce；懸空相電流參考值為零，電流實際值也為零，其反電勢系數是一個與轉子位置相關的量。設電機端電壓為u，那么根據式(27)無源性控制律可表示如下：

(28)

3 電機仿真與實驗結果

為驗證文中的無源性控制算法的控制效果，在MATLAB/Simulink平臺上搭建BLDCM的仿真模型。BLDCM的參數如下：極對數為4，等效電感L=2.565 mH，等效電阻R=0.5 Ω，轉動慣量為J=0.000 25 kg·m2，阻尼系數B=0.000 03 N·rad·s-1。其額定電壓為24 V，額定轉速為3 000 r/min。仿真過程中，設定的轉速n=2 000 r/min，在0到0.3 s時，電機空載運行，在0.3 s時對電機施加一個負載轉矩TL=0.1 N·m，可以得到電機的轉速變化曲線如圖2所示。圖3為電機0.3 s時的轉速仿真局部放大圖。

由圖2可以看出，無源性控制和PID控制都可以準確地跟蹤電機的轉速指令，但無源性控制在電機啟動時，能較快地達到設定轉速，沒有超調量，而PID控制會有較大的超調量；并且在0.3 s時刻電機受到突加負載轉矩的作用，電機轉速出現下降，從圖3電機轉速局部仿真圖中，可以明顯看到電機在無源性控制算法下，轉速下降較小，并能較快地恢復到設定轉速，而在PID控制算法下，轉速下降較大，對負載擾動較為敏感。仿真結果表明，無源性控制能保證系統的穩定運行，較好地跟蹤電機的轉速，實現對電機的轉速控制。

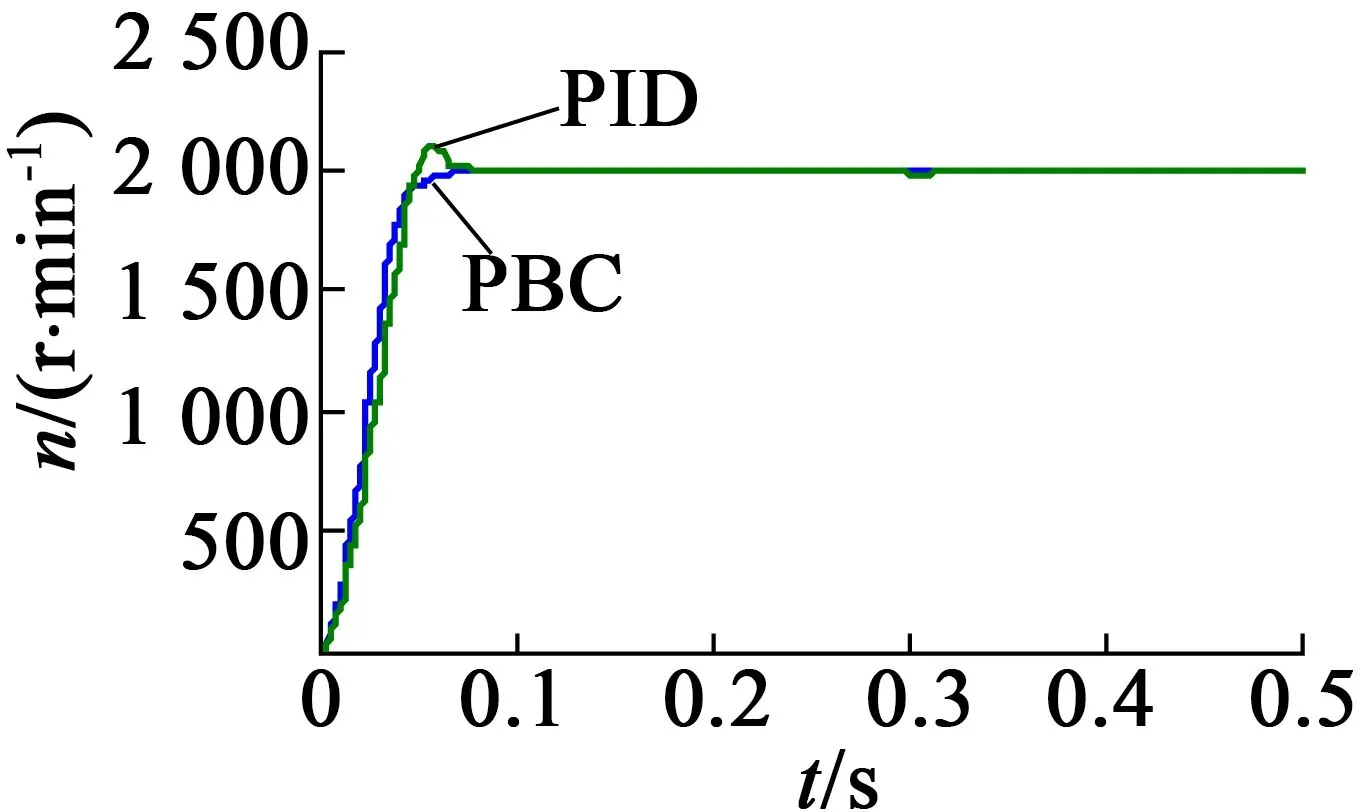
圖2 電機轉速仿真

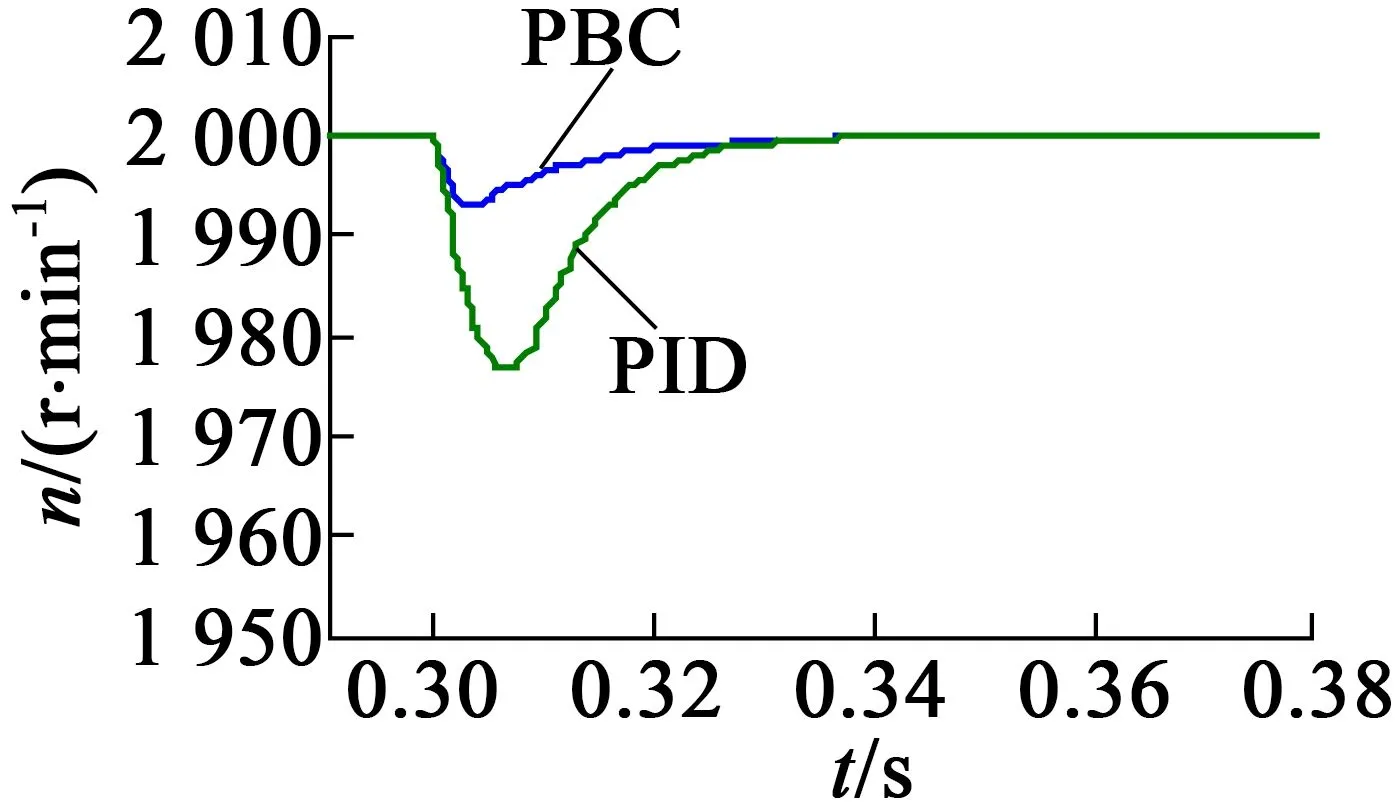
圖3 電機轉速仿真(局部)

本文通過dsPIC33芯片搭建的BLDCM控制系統對無源性控制算法進行驗證。電機控制系統由dsPIC控制器，三相驅動電路，檢測電路和BLDCM四部分構成。其結構如圖4所示。

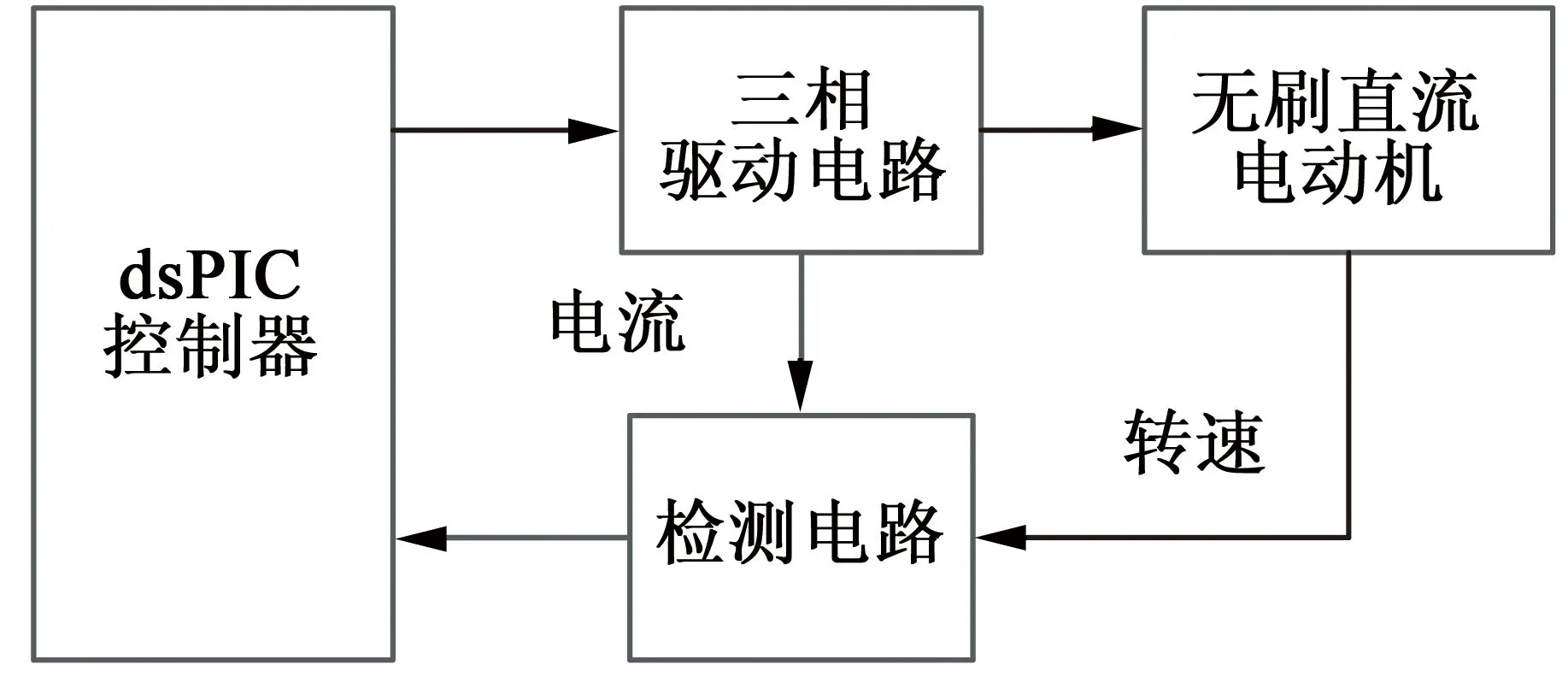
圖4 電機控制系統結構圖

在給定轉速n=2 000 r/min的條件下，分別得到BLDCM PID控制和無源性控制的轉速響應，如圖5和圖6所示。從兩者的轉速響應圖可以看出，無源性控制和PID控制都能穩定跟蹤系統設定的轉速，基本實現無穩態誤差。同時，無源性控制比PID控制有較短的響應時間，且電機轉速沒有超調。

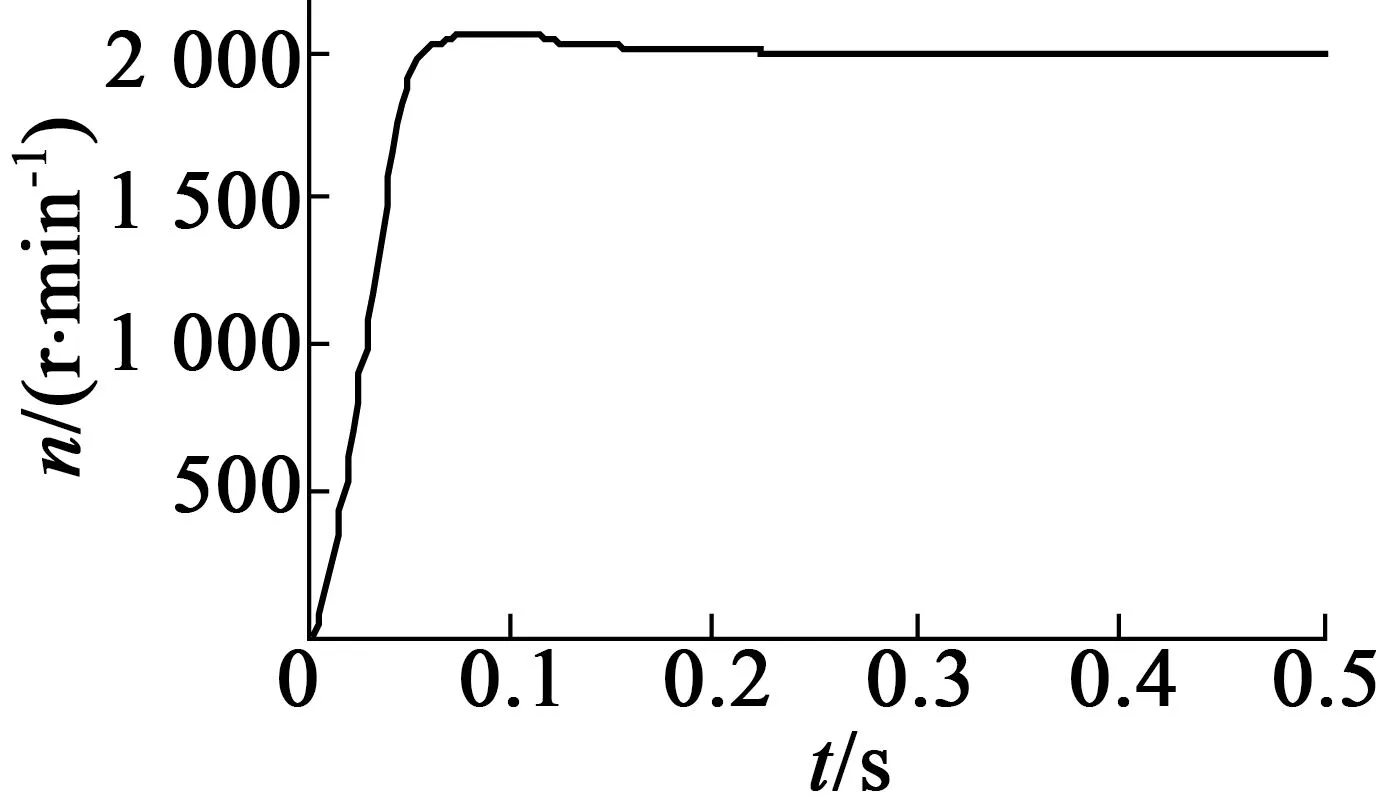
圖5 PID控制的電機轉速響應

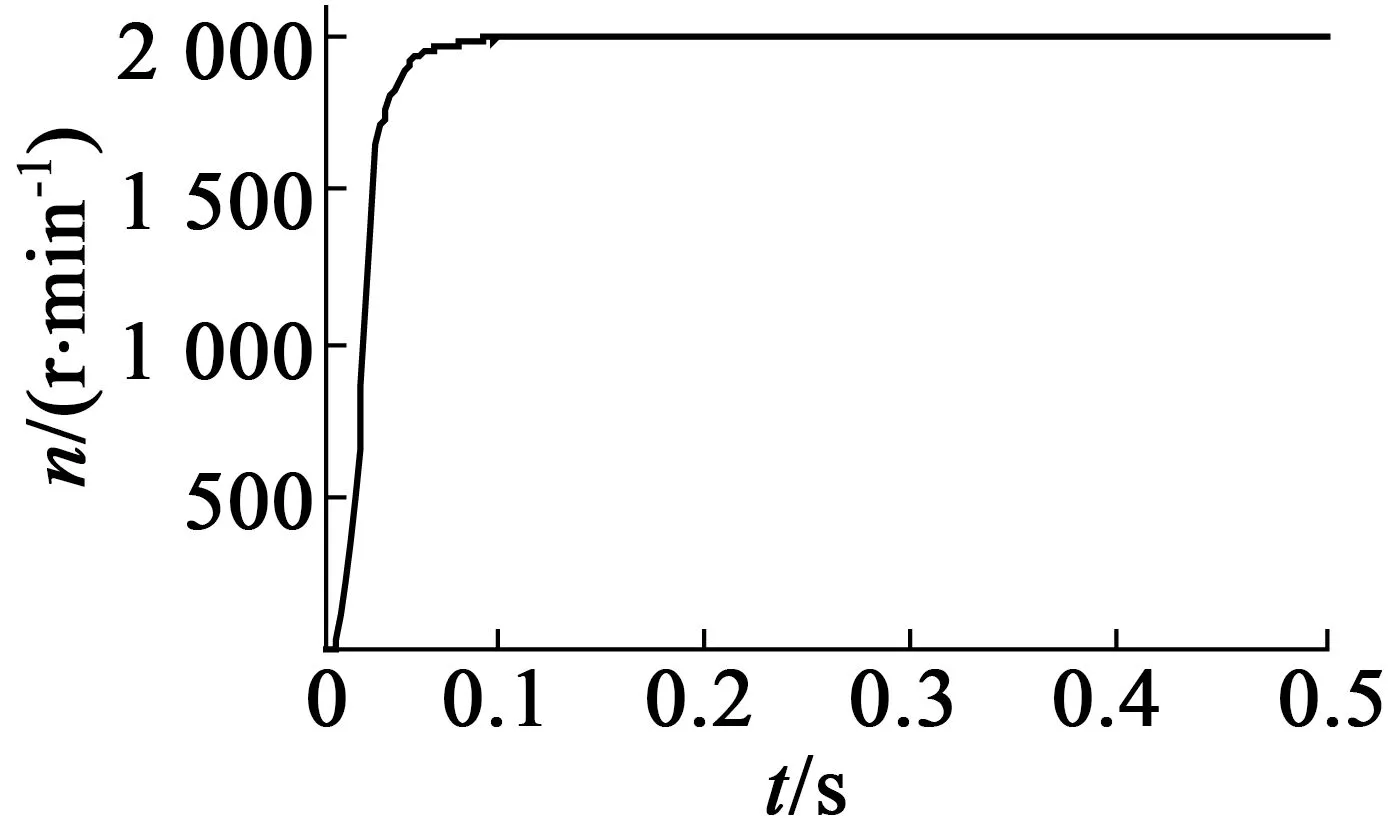
圖6 無源性控制的電機轉速響應

實驗結果表明，無源性控制算法能很好地跟蹤電機的轉速指令，其響應速度快，穩態誤差小。

4 結 語

無源性算法是一種非線性控制算法，它從系統狀態誤差的能量耗散去分析系統的穩定性，保證系統有全局穩定性。本文通過設計BLDCM進行無源性控制算法，并針對電機在實際運行過程中存在外加負載擾動的情況進行分析，采用負載擾動觀測器來提高控制系統的魯棒性。仿真與實驗證明，無源性控制器能很好地跟蹤電機設定轉速和較快的動態響應性能，對電機的負載擾動具有較強的魯棒性。

[1] 劉剛,王志強,房建成.永磁無刷直流電機控制技術與應用[M].北京:機械工業出版社,2008.

[2] 劉海珊,陳宇晨.無刷直流電動機PID控制系統仿真及實驗研究[J].系統仿真學報,2009,21(16):5157-5160.

[3] 夏長亮,郭培建,史婷娜,等.基于模糊遺傳算法的無刷直流電機自適應控制[J].中國電機工程學報,2005,25(11):129-133.

[4]NICKLASSONPJ,ORTEGAR,ESPINOSAPG,etal.Passivity-basedcontrolofaclassofBlondel-Parktransformableelectricmachines[J].IEEETransactionsonAutomaticControl,1997,42(5):629-647.

[5]ZHAOSW,CHEUNGNC,GANWC,etal.Passivity-basedcontroloflinearswitchedreluctancemotorswithrobustnessconsideration[J].ElectricPowerApplications,IET,2008,2(3):164-171.

[6] 廖冬初,陳力.鼠籠式感應電動機無源性轉速控制系統[J].微特電機,2013,41(5):1-3,8.

[7] 韓力,潘紅廣.無刷雙饋電機轉矩和轉速的無源性控制[J].電機與控制學報,2011,15(11):1-6.

Passive Based Speed Control for Brushless DC Motor

TANChuan-jie，YANGXiang-yu，ZHAOShi-wei

(South China University of Technology,Guangzhou 510640,China)

To improve the speed control performance of brushless DC motor, a speed control algorithm based on passivity theory was applied. The passivity of the control system of Brushless DC motor was analyzed, with the voltage equation, torque equation and motion equation of brushless DC motor. In order to improve the performance of the controller, a load disturbance observer was designed for compensating unknown load disturbances. A suitable control law can make the variables of the motor state error energy function converge to the desired value. Simulation and experiment show that the passive control has the advantages of simple control, good robustness and good performance for brushless DC motor.

brushless DC motor； passive based control； speed control； load observer

2016-03-02

TM33

A

1004-7018(2016)08-0122-04

譚傳接(1990-)，男，碩士研究生，研究方向為電氣傳動及其智能控制。