基于李雅普諾夫指數的臨近點選取方法

石鴻雁,魏俊達

(沈陽工業大學理學院,沈陽110870)

基于李雅普諾夫指數的臨近點選取方法

石鴻雁,魏俊達

(沈陽工業大學理學院,沈陽110870)

混沌時間序列的局域法預測以其計算量小、適用性強等優點,得到了廣泛應用。但是其預測效果受制于臨近點的選取,尤其是“偽臨近點”的存在將降低預測精度,所以合理選取臨近點至關重要。考慮到相點各維分量對預測的影響不同,相點的演化趨勢與其前S步相點存在相關性,文章利用最大李雅普諾夫指數構造權系數提出了基于李雅普諾夫指數的臨近點選取方法。通過Lorenz方程產生的混沌時間序列進行檢驗,結果表明改進方法的預測效果明顯提高。

混沌時間序列;局域法;臨近點;李雅普諾夫指數

0 引言

混沌時間序列預測模型在金融、氣象、交通、電力等諸多領域得到了廣泛的應用。目前學者們提出了多種混沌時間序列預測模型,根據擬合相點的不同,混沌時間序列預測可分為全域法和局域法。

全域法是將相空間中的所有相點作為參考點進行擬合預測。但是由于混沌系統的內部結構十分復雜,嵌入維數的增加,將導致擬合函數的計算復雜度急劇增加,模型的預測精度下降。因此,全域法只適用于空間結構簡單的系統。

與全域法不同的是,局域法預測思想是基于相空間中某一相點的未來演化趨勢與其臨近點的演化趨勢類似,將相空間軌跡的最后一點作為預測中心點,其空間鄰域內的相點作為臨近點,根據這些臨近點的演化趨勢f來預測未來演化相點。由于局域法預測具有計算量較小、擬合優度較高、適應性強等優點,因此局域法預測已經得到了廣泛的應用[1-3]。但是局域法預測效果依賴于臨近點的選取,通常僅根據歐氏距離來評價相點與預測中心點的空間位置關系,而沒有考慮相點間的演化趨勢易陷入“偽臨近點”,因此合理選取臨近點至關重要。

目前學者們提出了多種臨近點選取方法,文獻[4]在歐式距離的基礎上通過計算演化相點間的向量夾角,限制向量間的夾角來尋求相點間演化趨勢近似的臨近點。但是此方法將所有相點的演化趨勢籠統地限制在同一個區間內,對于距離較遠的臨近點,即使方向夾角較小,經過多步演化其演化趨勢也會產生較大的偏移,而導致“偽臨近點”的出現;文獻[5]考慮到高維空間中,歐氏距離無法充分描述相點間相似性的不足,利用參考相點與預測中心相點間的關聯度來選取臨近點。但是經過標準化的數據在后期計算過程中,會造成部分信息的丟失,無法體現下限參數對關聯度的影響。文獻[6]利用預測中心點的軌道和其臨近點軌道的分離指數來篩選臨近點,但是僅考慮了相點間的單步演化的近似關系而忽略了相點的多步演化趨勢,易誤將“偽臨近點”作為預測參考點,影響模型的預測精度。

考慮到混沌時間序列具有初值敏感性,傳統歐氏距離無法客觀反映相點各維分量對預測的影響,本文利用最大李雅普諾夫指數構造權系數對歐氏距離進行改進,將距離關聯度和向量夾角余弦作為相空間中相點間的空間關系和演化趨勢的評價標準,并根據相空間相點的演化趨勢與其前S步相點存在相關性的特點,通過追蹤前S步相點的演化趨勢,提出了基于李雅普諾夫指數改進的臨近點選取方法。利用Lorenz方程x分量產生的混沌時間序列進行仿真實驗,結果表明改進方法的預測效果明顯提高。

1 基礎理論

1.1 相空間重構

混沌時間序列的相空間重構理論[7]將一維原始時間序列拓撲映射到高維空間中,使得低維空間中無法充分挖掘的系統規律,在更高維空間中得以恢復和提取。因此相空間重構是混沌系統內在特性計算以及預測的基礎,相空間重構的效果直接影響到后續分析結果。

時間延遲τ和嵌入維數m是相空間重構中兩個重要參數。目前確定時間延遲和嵌入維數有兩種觀點[8],一種觀點認為時間延遲和嵌入維數互不相關,可以獨立確定,其中可通過復自相關法、互信息法等方法來確定延遲時間τ,通過關聯維數方法、虛假臨近點法等方法確定嵌入維數m;另一種觀點認為時間延遲和嵌入維數是相互關聯的,應該同步確定,這種觀點下的最典型方法是C-C方法[9]。

對于原始混沌時間序列{x(i),i=1,2,3,...,N},以時間延遲τ和嵌入維數m進行相空間重構得:

1.2 臨近點的常見選取方法

1.2.1 傳統歐氏距離法

最傳統的臨近點選取方法是歐式距離法,即根據相點間的歐式距離,在給定的γ鄰域空間內選取與中心相點距離最近的幾個相點作為參考點。

其中Xi是相空間中相點,XM是預測中心點,i≠M, γ為待定參數。

只追求歐式距離上的臨近而沒有考慮臨近點演化趨勢的近似,在經過幾次迭代后臨近點可能會偏離預測點的軌道,出現“偽臨近點”。如圖1,設預測中心點XM的臨近相點為XM1、XM2,其中:

XM的下一步演化相點為XM+1;XM1的下一步演化相點分別為XM1+1;XM2的下一步演化相點為XM2+1。雖然單步歐式距離上XM2與預測中心點XM更近,但是經過一步演化后XM2演化軌道與預測中心點XM的演化軌道明顯偏移,因此若將XM2作為臨近相點,勢必影響到模型的預測精度。

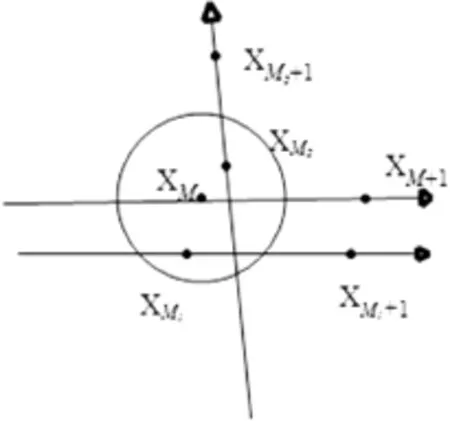
圖1 “偽臨近點”示意圖

此外,臨近點的數量與鄰域半徑γ的取值標準以及預測中心點的空間位置有著直接的關系。孟慶芳[10,11]利用統計學中的信息準則研究了不同臨近點數目對模型預測效果的影響,其思想是將滿足信息準則達到最低時的臨近點個數k作為標準。但是由于臨近點的數量受到原始數據多少等因素的影響,因此臨近點的數量只需在一定范圍內即可,即臨近點個數K∈[k-ε，k+ε]。

1.2.2 向量夾角余弦法

向量夾角余弦法是在傳統歐式距離方法的基礎上所提出的一種改進方法,此方法通過限制演化相點間的向量夾角來尋求相點間演化趨勢近似的相點。

設預測中心相點XM的前一步演化相點為XM-1,XM的臨近相點為XMi,其前一步演化相點為XMi-1,則夾角余弦為:

此方法就是通過限制δ的取值來篩選臨近點,既考慮了相點間距離上的臨近,又考慮到了演化趨勢上的近似。但是將所有臨近相點的演化趨勢籠統地限制在同一個區間內,不能完全剔除“偽臨近點”。如圖2,XM1和XM2是預測中心點XM的臨近相點,XM-1和XM+1分別是預測中心點XM的前一步演化點和下一步演化點;XM1-1,XM2-1和XM1+1,XM2+1分別是XM1,XM2的前一步演化點和下一步演化點, cosθM1M＜cosθM2M。對于臨近點距離較遠的相點XM2,即使方向夾角很小,經過多次演化后其演化軌跡也會與預測中心點的演化軌跡產生較大的偏移。顯然,如果利用XM2進行局域預測將極大地降低模型的預測精度。

圖2 “偽臨近點”示意圖

1.2.3 關聯度法

關聯度法[5]是將灰色理論與混沌時間序列相結合而提出的一種常用的臨近點選取方法,通過計算參考相點與預測中心相點間的關聯度來選取臨近點,一定程度上解決了傳統歐氏距離方法不能反映相點各維分量對預測影響的不足。設相空間中相點Xi的第k維元素為:

則相點Xi與相點XM之間的關聯度

關聯度法仍然存在不足之處,在進行數據標準化過程中,會造成下限參數的丟失,即因此無法體現下限參數對關聯度的影響[12]。

2 基于李雅普諾夫指數的臨近點選取方法

混沌時間序列具有初值敏感性的特點,即使初始點有微小的變化,其產生的兩個軌道之間的距離會呈李雅普諾夫指數分離。混沌時間序列之間的相關性隨著時間的變化而呈李雅普諾夫指數衰減。因此經過相空間重構之后,相點的各維分量對預測的影響是不同的,所以應根據時間間隔以及相點間各維衰減程度的不同,對各維分量的預測貢獻度進行合理加權。本文在文獻[12-14]的基礎上,對臨近點的選取方法做進一步的改進。

通過李雅普諾夫指數和延遲時間構造權系數對歐式距離進行修正:

ωi(n)是相點Xi的第n維分量的權重,n=1,…,m; ωi(n)=e-(m-n)λτ。

傳統關聯度方法在經過數據標準化后,無法體現下限參數對關聯度的影響,造成部分信息的丟失。為了解決以上不足,利用改進后的歐氏距離對傳統關聯度方法進行修正,得到距離關聯度:

其中,d(XMi,XM)通過式(5)計算。

綜合向量夾角余弦和距離關聯度,彌補單一評價指標描述相點間近似程度存在片面性的不足:

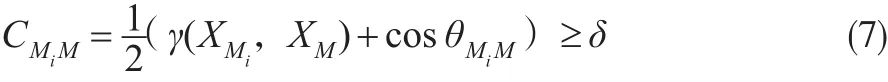
其中δ為約束參數;γ(XMi,XM)可描述相點間空間位置的近似程度;cosθMiM可描述相點間演化趨勢的近似程度。

對于不同的混沌時間序列,重構后的相點演化趨勢與其前S步相點存在相關性,僅根據相點間的單步演化關系不能完全剔除“偽臨近點”,因此通過追蹤前S步相點的演化趨勢,對式(7)進行修正。

設相點XMi是XM的臨近相點,XMi-S-1和XMi-S分別是XMi的前S-1步和前S步演化相點,XM-S-1和XM-S分別是XM的前S-1步和前S步演化相點,則其構成的向量夾角cosSθiM為:

第S步的評價函數為:

進而得到S步演化相點評價函數:

若r=0,則規定ωS=1;λ為最大李雅普諾夫指數。評價函數值小于δ的相點被視為“偽臨近點”予以剔除,而δ的取值根據原始數據和模型的預測精度要求確定。

修正后的式(10),同時兼顧了相點間空間位置以及相點間演化趨勢,并根據演化相點的相關性,通過追蹤前S步相點的演化趨勢進一步剔除“偽臨近點”,因此可利用式(10)選取臨近點。

3 實驗仿真

為了檢驗選取的臨近點對模型預測效果的影響,本文通過Lorenz方程x分量產生的混沌時間序列對原方法和改進方法進行對比檢驗。Lorenz方程為:

取初值x(0)=-1，y(0)=0，z(0)=1,參數a=16，b=4，c= 45.92,時間步長為0.01。

由Lorenz方程x分量產生的第10001到13010個數據,前3000個數據作為擬合數據,后10個作為檢驗數據。

選取均方誤差(MSE)作為性能評價指標,其公式如下式:

經計算,混沌時間序列的延遲時間τ=10,嵌入維數m=6。對原始時間序列進行相空間重構后,分別利用傳統方法和改進方法選取臨近點,并采用局域平均法和加權一階局域法對樣本進行遞歸多步預測。

利用改進方法選取臨近點,取S=3,r=4,約束參數δ=0.85,IMiM值小于0.85的相點視為“偽臨近點”,予以剔除。采用局域平均法和加權一階局域法對樣本進行遞歸多步預測。實驗結果如圖3和圖4所示。

圖3 局域平均法預測誤差對比圖

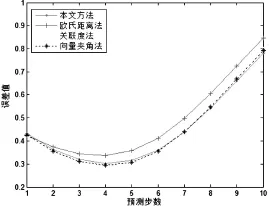
圖4 加權一階局域法預測誤差對比圖

由圖3可知,改進的方法和關聯度方法的預測均方誤差總體相對平緩,并且經過改進的臨近點選取方法,其預測誤差較其他方法有明顯的降低,說明改進后的方法,可有效篩選臨近點,提高局域法預測精度。而從圖4和表1可以看出,基于不同的臨近點選取方法的一階加權局域預測法,隨著預測步數的增加其預測均方誤差均呈現先下降后上升的趨勢,當預測步數小于5步時,改進方法的均方誤差略高于傳統方法,但是隨著預測步數的增加其預測效果好于傳統方法。

表1 不同方法間的誤差對比

4 結論

本文根據混沌時間序列具有初值敏感性的特點,通過李雅普諾夫指數構造權系數對傳統歐氏距離進行改進,利用距離關聯度和向量夾角余弦的平均值對相空間中相點間的空間關系和演化趨勢進行綜合評價,并考慮到單步演化關系不能完全剔除“偽臨近點”的不足,根據演化相點的相關性,通過向追蹤前S步相點演化趨勢,提出了基于李雅普諾夫指數改進的臨近點選取方法。利用Lorenz方程x分量產生的混沌時間序列進行仿真實驗,結果表明改進后的預測精度比其他傳統方法有了明顯提高,改進后的方法選取臨近點的合理性和有效性,為混沌時間序列的局域法的應用打下了堅實基礎。

[1]Abdollahzade M,Miranian A,Hassani H,et al.A New Hybrid Enhanced Local Linear Neuro一fuzzyModel Based on TheOptimized Singular Spectrum Analysis and Its Application For Nonlinear and Chaotic Time Series Forecasting[J].Information Sciences,2015,295.

[2]殷禮勝,何怡剛,董學平等.交通流量vNNTF神經網絡模型多部預測研究[J].自動化學報,2014,40(9).

[3]侯公羽,梁榮,孫磊等.基于多變量混沌時間序列的煤礦斜井TBM施工動態風險預測[J].物理學報,2014,63(9).

[4]唐巍,谷子.基于相關鄰近點與峰谷荷修正的短期負荷時間序列預測[J].電力系統自動化,2006,30(14).

[5]Jiang C,Li T.Forecasting Method Study on Chaotic Load Seriesw ith High Embedded Dimension[J].Energy Conversion and Management, 2005,46(5).

[6]王揚,張金江,溫柏堅等.風電場超短期風俗預測的相空間優化鄰域局域法[J].電力系統自動化,2011,35(24).

[7]呂金虎,陸君安,陸士華.混沌時間序列分析及應用[M].武漢:武漢大學出版社,2005.

[8]高俊杰.混沌時間序列預測研究及應用[D].上海:上海交通大學學位論文,2013.

[9]陸振波,蔡志明,姜可宇.基于改進的C一C方法的相空間重構參數選擇[J].系統仿真學報,2007,19(11).

[10]孟慶芳,彭玉華,曲懷敬等.基于信息準則的局域法臨近點的選取方法[J].物理學報,2008,57(3).

[11]Meng Q F,Chen y H,Feng ZQ,etal.Nonlinear Prediction of Small Scale Network Traffic Based on Local Relevance vector Machine Regression Model[J].Chinese PhysicalSoc,2013,62(15).

[12]裴玲玲,王正新,沈春光.灰色距離關聯度模型及其性質研究[J].統計與決策,2010,(16).

[13]王振朝,趙晨等.用于混沌時間序列預測的分維指數加權一階局域算法[J].電測與儀表,2010,533(47).

[14]Qu J L,w ang X F,Qiao y C,et al.An Improved Local w eighted Linear Prediction Model for Chaotic Time Series[J].Chinese Physics Letters,2014,31(2).

(責任編輯/亦民)

N941.7

A

1002-6487(2016)20-0012-04

石鴻雁(1962—),女,遼寧沈陽人,博士,教授,研究方向:時間序列分析。魏俊達(1990—),男,黑龍江哈爾濱人,碩士研究生,研究方向:時間序列分析。