一種改進的B樣條翼型參數化方法

張 驥， 朱春鋼， 馮仁忠， 劉明明， 張恒洋

(1. 大連理工大學數學科學學院，遼寧 大連 116024；2. 北京航空航天大學數學與系統科學學院，北京 100083)

一種改進的B樣條翼型參數化方法

張 驥1， 朱春鋼1， 馮仁忠2， 劉明明1， 張恒洋1

(1. 大連理工大學數學科學學院，遼寧 大連 116024；2. 北京航空航天大學數學與系統科學學院，北京 100083)

翼型設計是空氣動力學研究的一項重要內容，翼型的參數化結果將影響翼型的優化設計。為了減少翼型優化中的設計變量，保證優化結果的光滑性與C2連續，在優化過程中控制翼型幾何特性的變化范圍，提出了一種改進的B樣條參數化方法。用一條三次非均勻B樣條曲線表示翼型，翼型數據的參數化過程中主要運用了B樣條曲線擬合算法，并且在一般的B樣條曲線擬合算法的基礎上加入了對曲線的法向約束，通過迭代得到最終的參數化結果。實驗結果表明，該方法可以很好的擬合典型的翼型數據，得到的翼型參數化結果不僅光滑，滿足 C2條件，而且所得翼型函數的參數個數比傳統的參數化方法有了進一步的減少，更有利于之后翼型的優化設計。

翼型；B樣條曲線；翼型參數化；翼型優化

翼型設計是空氣動力學研究的一項重要內容，翼型作為飛行器翼面部件的截面形狀，其幾何外形設計對整個翼面部件甚至是整個飛行器的性能均存在重要影響。隨著現代飛行器的設計要求越來越多，性能目標不斷提高，在設計過程中必須對飛行器的幾何外形進行精細化設計，因此對翼型的設計優化提出了更高的要求。為了縮短研發周期，降低研發費用，將基于氣動性能數值計算的翼型優化設計方法與風洞實驗相結合已成為目前翼型研究的發展方向[1-2]。

為了實現基于數值計算的翼型優化，需要給出相應的翼型參數化方法，即用含參數的翼型函數擬合由離散數據點表示的待優化翼型，再選擇翼型函數的適當參數作為設計變量，結合優化算法與流場計算實現優化設計。在氣動優化過程中，翼型參數化方法的選擇除了影響優化算法類型的選擇外，還影響計算時間和資源，設計空間的范圍及設計空間中翼型幾何外形是否光滑，設計空間中是否包含有意義的優化結果，在保持結果有足夠的自由度和光滑性的前提下盡可能的減少設計變量。在設計優化過程中，減少翼型的幾何表示參數可以簡化設計過程。因此需要采取合適的翼型參數化方法產生連續光滑的翼型幾何外形[3]。

現在典型的參數化方法主要包括Hicks-Henne外形函數法[4]、PARSEC參數化方法[5]、CST翼型參數化方法[6]和樣條參數化方法[7]。Hicks-Henne外形函數法具有很強的翼型外形控制能力；PARSEC參數化方法設計參數較少(11個)，具有較好的魯棒性；CST翼型參數化方法能夠描述較大的設計空間；樣條參數化方法主要指通過 Bézier曲線、B樣條曲線或非均勻有理B樣條(NURBS)曲線表示翼型曲線的方法，能夠對曲線外形進行局部控制和光滑處理，如 Deng和 Feng[8]在 2011年提出的由4條首尾相接的有理Bézier曲線表示超臨界翼型的參數化方法。

隨著航空計算的快速發展，上述方法在某些方面已經無法滿足現代飛行器外形的精細化設計需求：如Hicks-Henne外形函數法，優化結果存在不光滑現象；PARSEC參數化方法對翼型外形控制能力差，不適用于精細化設計；CST翼型參數化方法魯棒性差，對超臨界翼型擬合效果不理想；而Ferguson樣條法[9]所得到的翼型函數不滿足C2條件。

B樣條方法在幾何外形設計中有著廣泛的應用[10]，其中三次B樣條曲線以其次數不高、滿足C2連續性等良好性質而成為最常用的曲線設計方法。利用 B樣條方法對于翼型進行參數化設計，曲線的局部調整性有利于之后的翼型優化設計，由于 B樣條曲線可以很容易擴展到三維空間，更有利于機翼曲面參數化設計。2008年，Brakhage 和Lamby[11]對B樣條方法進行翼型參數化進行了較為詳盡的介紹。本文提出一種改進的 B樣條翼型參數化方法，在一般的 B樣條方法的基礎上加入了法向約束，最終用一條四段三次非均勻 B樣條曲線表示翼型曲線。得到的翼型曲線的參數個數比一般的 B樣條方法有了進一步的減少，所得翼型曲線光滑且滿足C2條件。

1 B樣條參數化方法

定義 1[12]. 設 n+1個平面向量， Ni,p (t)是定義在節點向量上的p次 B樣條基函數(n≥p)，則稱：

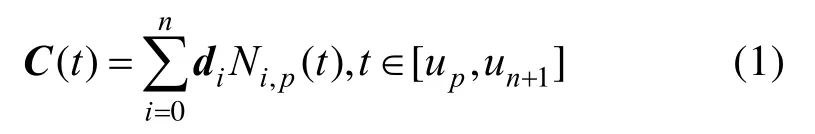
為相應于節點向量U的p次B樣條曲線，稱di為控制頂點，順序連接 d0,…,dn的折線段為控制多邊形。

由于三次B樣條曲線是應用最廣泛的B樣條曲線，本文方法采用一條四段三次非均勻 B樣條曲線表示翼型曲線。根據如上B樣條曲線的定義，曲線 C (t)定義為：

其中定義樣條基函數的節點向量為：

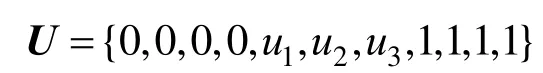
其中， u1,u2,u3待定。此節點向量U確保了曲線C (t)在兩端插值于首末控制頂點d0與d6。

1.1 目標函數

翼型的參數化就是反求 B樣條曲線 C (t)，即根據已知的翼型數據點設計優化目標函數，反求曲線 C (t)的控制頂點，本文采用的優化目標函數為：

表示給定的數據點，C′(ti)表示曲線在點 C (ti)處的切向量，ni表示數據點pi處的單位法向量，X是設計參數向量，即曲線的控制頂點的坐標。根據式(2)，可得：

其中，Nj,3(t)是三次B樣條基函數，為C(t)的控制頂點，因此可得：

目標函數 F(X)第一項表示數據點到參數曲線上距離的平方和，保證了參數化曲線與數據點擬合的整體效果；第二項為法向約束，表示數據點的法線向量與參數曲線的切線向量的內積和，確保參數曲線的切線向量與數據點的法向盡量垂直。λ為權系數，可以在區間［0,1］調節，但第一項為主項，λ不宜過大，經過實驗將λ取做0.13。

1.2 數據點的法向量估計

為了求解目標函數式(3)，需要首先估計數據點的法向量。簡單的估計方法可以用數據點相鄰兩點的連線的垂線近似數據點的法向，但此方法產生的誤差較大。本文利用Jüttler和Felis[13]提出的方法來估計數據點的法向。

如圖1所示，方法主要分為2步：

(1) 對于點pi計算局部相關回歸線Li，即求解帶權的最小二乘問題：

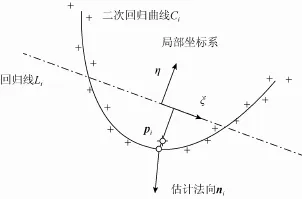
圖1 估計數據點法向量

(2) 選取一個新的笛卡爾坐標系，以pi為原點，x軸平行于Li，用二次回歸曲線Ci逼近數據點，這條曲線是新坐標系下的一條二次曲線，通過求解：

其中，pnj表示新坐標系下的數據點的坐標，可用二次曲線Ci在原點的法向量近似pi的法向量ni。為了使翼型曲線在前緣滿足切線方向垂直于x軸，使最左端前緣數據點的法向平行于x軸，估計出翼型數據點的法向量(圖2)。

圖2 翼型數據點的法向量

1.3 數據的初步處理

(1) 對給定的翼型數據點進行初步處理，將控制頂點d0設為翼型后緣上表面最后一個數據點的坐標值，再將控制頂點d6設為翼型后緣下表面最后一個數據點的坐標值。剩下需要確定的是控制頂點d1,…,d5。再利用1.2節的方法，估計各數據點對應的法向量。

(2) 由累加弦長法[14]，預估數據點對應的參數，即將數據點對應到參數區間［］0,1上，得到相應參數，并且令t0= 0,tn=1。將節點向量中的u1設為翼型上弧線最高點的參數值，u2設為翼型前緣頂端數據點的參數值，u3設為翼型下弧線最低點的參數值。

1.4 確定控制頂點坐標

通過初步處理已經確定了曲線的首末控制頂點，剩下需要確定的是控制頂點 d1,…,d5，即通過優化1.1節中所給出的目標函數式(3)的過程，使其取得最小值：

其中，等式右端第一項

關于xdk求偏導有(k=1,…,5)：

利用B樣條曲線的定義，式(5)右端第二項在節點區間ti∈[Uq,Uq +1]上有(其中Uq表示節點向量第q個節點的值，其中q取3～6)：

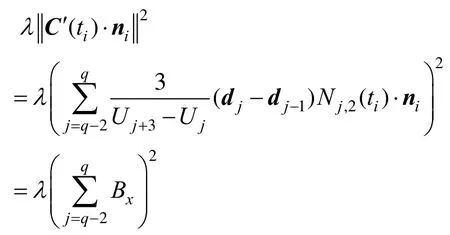
其中，

關于xdk求偏導有：

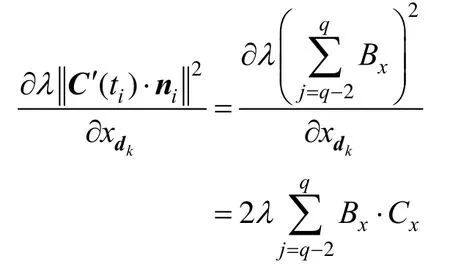
其中

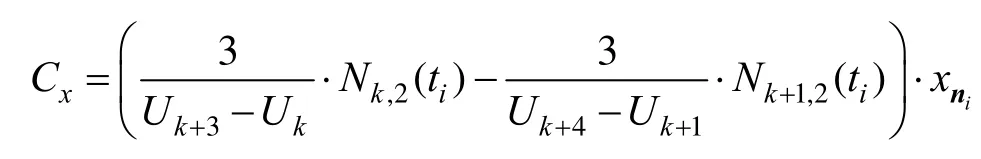
綜上，F(X)對關于xdk求偏導有：

同理可得：

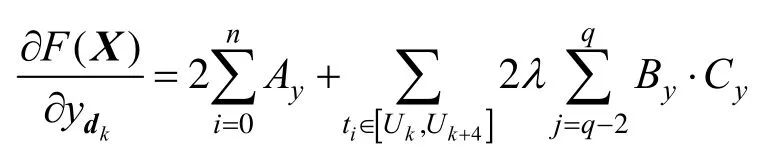
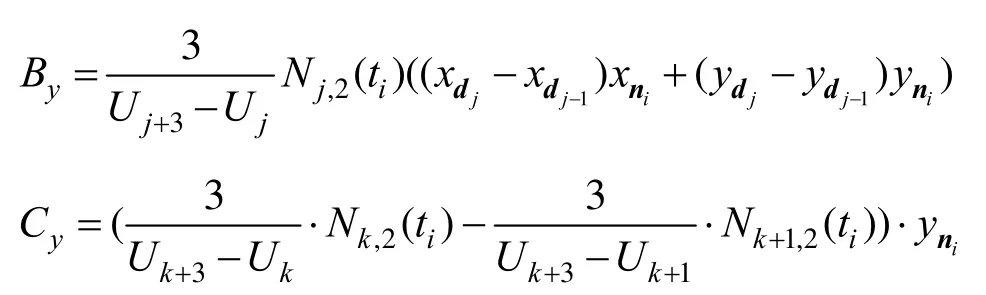
令 F(X)關于xdk,ydk(k=1,…,5)的偏導數為零，得到法方程組：

式(6)為含有10個未知數10個方程的方程組，通過求解可以得到控制頂點的坐標從而確定控制頂點。

1.5 誤差計算和參數的重新選擇

誤差是衡量參數化結果好壞的標準，本文中所給的誤差均指在翼型弦長為1時各數據點到參數曲線的距離之中的最大值。此外由于數據點的參數化對曲線的形狀以及擬合效果具有非常重要的作用，而初始的參數化方法并不一定理想，因此在初始計算的基礎上需要對數據點重新參數化并重新計算控制頂點以改善擬合效果，而重新參數化數據點的過程可以與計算擬合誤差同步進行。

本文使用基于幾何特征的快速迭代法[15]計算點到曲線的距離。如圖 3所示，求一點p到曲線C(t)的距離，即希望找到滿足 C(t)與p之間距離最小的參數tp，一般根據幾何關系可知，矢量ρ=(p-C(tp))必須與曲線在C(tp)點處的切線方向垂直，即滿足(p-C (tp))·C′(tp)=0，其中。此方法通過給定初始參數值tp,0，通過迭代逐漸逼近tp。其算法如下：

圖3 點到曲線的距離

在計算誤差過程中同時更新數據點的參數值，用tp替代數據點的原參數值，再用1.4節的方法求出在新參數值下的新控制頂點，重復1.4節與1.5節的方法，直到誤差收斂。此時得到的即為最終的翼型函數。

2 算法與實例

圖4為利用三次非均勻B樣條曲線進行翼型參數化的算法流程圖。采用圖 4所示的算法，對EPPLER 398翼型進行參數化。表1給出具體的迭代次數以及每次迭代后的擬合誤差。

圖4 算法流程圖

表1 計算次數與誤差

從表1中可以看出，誤差在第343次計算達到收斂，至此也就確定了參數曲線的控制頂點坐標。翼型的參數化過程見圖5。

圖5 EPPLER 398翼型的參數化過程

將這種參數化方法應用于其他一些典型的翼型數據。圖6是對NACA 65(2)-215翼型的參數化過程，表 2給出了一些典型翼型的參數化誤差，以及參數化的計算時間(算法在 VS2013平臺使用C++編程實現，這里的計算時間均是在CPU頻率為3.20 Hz，內存為4 GB的PC機上運行得出)。

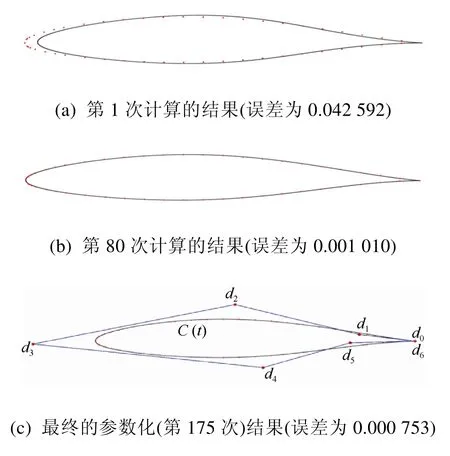
圖6 NACA 65(2)-215翼型的參數化過程

表2 各翼型函數的誤差與計算時間

由表1發現，雖然最終翼型函數的誤差較小，但誤差的收斂速度比較慢。經過實驗，對于一般的翼型一般需要迭代 300～400次才能收斂。但本文方法的計算時間是可以控制的，從表 2可以看出，一般翼型的參數化都可以在1 s左右得出結果。

表3 RAE 2822翼型的參數化結果

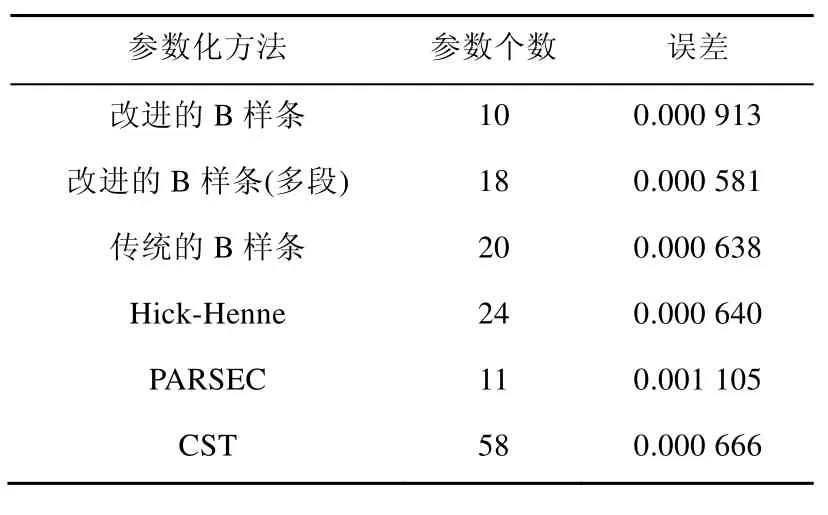
表4 NACA640-110翼型的參數化結果

3 結論與展望

根據實驗結果，對于大多數翼型，本文方法的擬合精度可達到 10–3～10–4，滿足機翼外形曲線擬合以及隨后生成機翼參數曲面的要求，所得到的翼型函數具有多項優點：光滑且滿足C2條件、函數所含的設計變量較少(共 10個)、可以在較短時間內收斂到參數化結果。

但為了達到氣動力性能設計的要求，擬合誤差需要小于 7×10–4，即翼型的精確表示[11]。將本文方法簡單推廣到多段(多于四段)[16]，就可以得到一般的改進翼型三次 B樣條參數化方法，達到精確表示翼型的要求。表3和表4分別給出了RAE 2822翼型和NACA64-110翼型利用本文算法和典型參數化方法[17]的參數化結果。對比可以發現本文所提出的改進的 B樣條參數化方法的參數個數明顯少于傳統的參數化方法，而將本文方法推廣得到的多段改進 B樣條參數化方法不僅可以滿足氣動力性能設計的要求，而且在擬合精度和參數個數方面都比傳統的參數化方法有所提高。

在接下來的工作中，將進一步改進算法，增加能量約束[18]，并將算法推廣，使得算法可以根據翼型數據點規模和曲率自適應選取 B樣條曲線控制頂點個數(即分段數)，從而達到氣動力性能設計的要求。最后還將把算法推廣到三維上，用 B樣條曲面對飛行器翼面進行擬合，從而給出機翼的函數表示。

[1] 劉 周, 朱自強, 付鴻雁, 等. 高升阻比翼型的設計[J]. 空氣動力學學報, 2004, 22(4): 410-414.

[2] 王曉璐, 朱自強, 劉 周, 等. 基于N-S方程的翼型雙設計點雙目標優化設計[J]. 北京航空航天大學學報, 2006, 32(5): 503-507.

[3] Song W, Keane A J. A study of shape parameterization methods for airfoil optim ization, AIAA 2003-4482 [R]. Reston: American Institute of Aeronautics and Astronautics, 2004.

[4] Hicks R M, Hennet P A. Wing design by numerical optim ization [J]. Journal of Aircraft, 1978, 15(7): 407-412.

[5] Sobieczky H. Parametric airfoils and wings [M]//Notes on Numerical Fluid Mechanics (NNFM): Recent Development of Aerodynamic Design Methodologies. Germany: Vieweg Teubner Verlag, 1990: 71-87.

[6] Kulfan B M, Bussoletti J E. “Fundamental” parametric geometry representations for aircraft component shapes, AIAA 2006-6948 [R]. Reston: American Institute of Aeronautics and Astronautics, 2006.

[7] Lepine J, Guibauh F, Trepanier J Y, et al. Optim ized nonuniform rational B-spline geometrical representation for aerodynam ic design of w ings [J]. American Institute of Aeronautics and Astronautics, 2001, 39(11): 570-577.

[8] 鄧金秋, 馮仁忠. 利于翼型優化設計的超臨界翼型參數化方法[J]. 北京航空航天大學學報, 2011, 37(5): 368-373.

[9] Sobester A, Keane A J. Airfoil design via cubic splines –Ferguson’s curves revisited, AIAA 2007-2881 [R]. Reston: American Institute of Aeronautics and Astronautics, 2007.

[10] 夏成林, 鄔弘毅, 鄭興國, 等. 帶多個形狀參數的三次均勻B樣條曲線的擴展[J]. 圖學學報, 2011, 32(2): 73-79.

[11] Brakhage K H, Lamby P. Application of B-spline techniques to the modeling of airplane w ings and numerical grid generation [J]. Computer Aided Geometric Design, 2008, 25(9): 738-750.

[12] 王仁宏, 李崇君, 朱春鋼. 計算幾何教程[M]. 北京:科學出版社, 2008: 158-174, 188-200.

[13] Jüttler B, Felis A. Least-squares fitting of algebraic spline curves via normal vector estimation [J]. Advances in Computational Mathematics, 2002, 17(1): 135-152.

[14] Farin G E. Curves and surfaces for computer-aided geometric design [M]. San Diego: Academ ic Press, 1997: 53-56, 172-224 .

[15] 伍麗峰, 陳岳坪, 諶炎輝, 等. 求點到空間參數曲線最小距離的幾種算法[J]. 機械設計與制造, 2011, (9): 15-17.

[16] 韓力文, 楊玉婷, 邱志宇. 一種任意次非均勻 B 樣條的細分算法[J]. 圖學學報, 2013, 34(5): 56-61.

[17] 張德虎, 席 勝, 田 鼎. 典型翼型參數化方法的翼型外形控制能力評估[J]. 航空工程進展, 2014, 5(3): 281-288.

[18] 徐 進. 帶約束的B 樣條曲線曲面延伸技術[J]. 圖學學報, 2013, 34(3): 36-42.

An Improved Method for Airfoil Parameterization by B-Sp line

Zhang Ji1, Zhu Chungang1, Feng Renzhong2, Liu Mingm ing1, Zhang Hengyang1

(1. School of Mathematical Sciences, Dalian University of Technology, Dalian Liaoning 116024, China; 2. School of Mathematics and Systems Science, Beihang University, Beijing 100083, China)

Airfoil design is a crucial issue of aerodynam ic research, the parameterization of airfoil will affect the airfoil optimization design. In order to reduce the number of variables in the airfoil optim ization, eliminate the unfairness phenomenon, preserve the C2continuity condition, and control the geometric characteristics of the airfoil in the optim ization process, in this paper, we present an improved method for airfoil parameterization by B-spline. The method represents airfoil by a cubic non-uniform B-spline curve. Fitting of airfoil data by B-spline curve is mainly by least square method and the normal constraints. And the final result is obtained by iteration. Experiments show that the proposed method can be well fitted to the typical airfoil data, the resulting curve is fair and C2continuity, and has few parameters of airfoil function compared with the classical airfoil parametric methods.

airfoil; B-spline curves; airfoil parameterization; airfoil optim ization

TP 391

10.11996/JG.j.2095-302X.2016030342

A

2095-302X(2016)03-0342-07

2015-11-05；定稿日期：2015-12-01

國家自然科學基金項目(11271060, 11290143)；民用飛機專項項目(MJ-F-2012-04)；中央基本科研業務費資助項目(DUT16LK38)；遼寧省高等學校優秀人才支持計劃項目(LJQ2014010)

張 驥(1990–)，男，江蘇鹽城人，碩士研究生。主要研究方向為計算幾何。E-mail：jizhang1990@gmail.com

朱春鋼(1977–)，男，北京人，教授，博士。主要研究方向為計算幾何與計算機輔助幾何設計。E-mail：cgzhu@dlut.edu.cn