4.1等可能性
趙利俠

新課程標(biāo)準(zhǔn)指出,教師是學(xué)生學(xué)習(xí)的組織者、指導(dǎo)者、引領(lǐng)者,是平等對(duì)話的首席。在課堂上,我們應(yīng)該做一個(gè)優(yōu)秀的“導(dǎo)演”,教師的理想是“一切為了學(xué)生的未來發(fā)展著想”,這往往需要我們?cè)谡n堂上給學(xué)生充分的時(shí)間和空間創(chuàng)造更多的機(jī)會(huì),搭建更多展示的舞臺(tái),真正讓學(xué)生成為學(xué)習(xí)的主人,放手讓他們?nèi)ヌ骄浚屗麄儺a(chǎn)生更多的“?”,讓他們自己想辦法分析和解決問題。同時(shí)不忘在學(xué)生需要幫助的時(shí)候扶他們一把,給予正確的指導(dǎo)和點(diǎn)撥。另外,教師還要善于發(fā)現(xiàn)學(xué)生學(xué)習(xí)過程中的細(xì)波微瀾,進(jìn)而推波助瀾。這樣學(xué)生才會(huì)有更多的收獲,更多的“!”。
【教學(xué)目標(biāo)】
1.會(huì)列出一些類型的隨機(jī)試驗(yàn)的所有可能結(jié)果(基本事件);
2.理解等可能的意義,會(huì)根據(jù)隨機(jī)試驗(yàn)結(jié)果的對(duì)稱性或均衡性判斷試驗(yàn)結(jié)果是否具有等可能性。
【教學(xué)重難點(diǎn)】
【重點(diǎn)】理解等可能概念的意義,會(huì)根據(jù)隨機(jī)試驗(yàn)結(jié)果的對(duì)稱性或均衡性判斷試驗(yàn)結(jié)果是否具有等可能性。
【難點(diǎn)】理解等可能概念的意義,會(huì)列出一些類型的隨機(jī)試驗(yàn)的所有可能結(jié)果。
【教學(xué)過程】
教學(xué)過程(教師)
問題情境
情境1:老師手里拿了一塊糖,在不知道的情況下,糖在左手還是右手?糖在左手是一個(gè)什么事件?糖能否既在左手又在右手呢?糖在左手的可能性大還是右手的可能性大?
情境2:一只不透明的袋子中裝有3塊除顏色外都相同的糖,顏色分別是紅色、黃色、藍(lán)色,攪勻后從中任意摸出1塊糖,會(huì)出現(xiàn)哪些可能的結(jié)果?這些結(jié)果出現(xiàn)的可能性一樣嗎?
變式:將其中的一塊藍(lán)色糖換成紅色,此時(shí)袋中有一黃兩紅,摸到黃色則男生獲得獎(jiǎng)勵(lì),摸到紅色的則女生獲得獎(jiǎng)勵(lì),你們同意嗎?
情境3:一枚質(zhì)地均勻的骰子,6個(gè)面分別標(biāo)上1~6這6個(gè)數(shù),拋擲一次,會(huì)出現(xiàn)哪些可能的結(jié)果?這些結(jié)果的出現(xiàn)是等可能的嗎?
情境4:如圖所示,當(dāng)轉(zhuǎn)盤停止轉(zhuǎn)動(dòng)時(shí),指針落在三種顏色區(qū)域上的可能性一樣嗎?
學(xué)生活動(dòng)
仔細(xì)閱讀,積極思考,踴躍回答:
1.在左手或在右手,隨機(jī)事件,不可能,一樣大。
2.會(huì)出現(xiàn)3種可能的結(jié)果:摸出黃色糖,摸出紅色糖,摸出藍(lán)色糖。
變式:不同意,將紅色糖分別標(biāo)為1,2。
3.會(huì)出現(xiàn)6種可能的結(jié)果:正面朝上分別是:1,2,3,4,5,6,這6個(gè)數(shù)中的任意一個(gè)。
4.指針落在兩種顏色區(qū)域上的可能性不一樣。
設(shè)計(jì)思路
在本章第一節(jié)新授課中,呈現(xiàn)本章節(jié)的典型情境。
四個(gè)情境,分別從正反兩方面讓學(xué)生充分感悟事件的等可能與不等可能,為后續(xù)學(xué)習(xí)奠定基礎(chǔ)
探索活動(dòng)
歸納小結(jié):一般的,設(shè)一個(gè)試驗(yàn)的所有可能發(fā)生的結(jié)果有n個(gè),它們都是隨機(jī)事件,每次試驗(yàn)有且只有其中的一個(gè)結(jié)果出現(xiàn)。如果每個(gè)結(jié)果出現(xiàn)的機(jī)會(huì)均等,那么我們說這n個(gè)事件的發(fā)生是等可能的,也稱這個(gè)試驗(yàn)的結(jié)果具有等可能性。
反思、提煉,形成概念。
舉例、交流。
從豐富的情境中提煉出等可能性的基本特征。
讓學(xué)生通過充分交流、討論、探究,深化了對(duì)等可能意義的理解,發(fā)展了學(xué)生的數(shù)學(xué)能力。
讓學(xué)生嘗試舉例,感悟事件的等可能與不等可能,加強(qiáng)對(duì)事件等可能性的理解。
例題講解
例1:從一名男生和兩名女生中任選一名學(xué)生,幫助學(xué)校圖書館整理圖書,會(huì)有哪些可能的結(jié)果?這些結(jié)果是等可能的嗎?
例2:A、B兩地之間的電纜有一處斷點(diǎn),斷點(diǎn)出現(xiàn)在電纜的各個(gè)位置的可能性相同嗎?
例題選講,規(guī)范答題格式。
關(guān)注事件描述的完整性,為后續(xù)事件的規(guī)范描述作鋪墊。
拓展延伸
1.感受四個(gè)問題情境,它們有怎樣的內(nèi)在聯(lián)系呢?
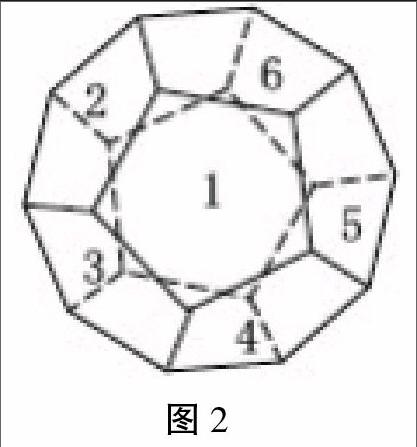
2.如圖2,拋擲一個(gè)質(zhì)地均勻的正十二面體,12個(gè)面上分別標(biāo)有1-12這12個(gè)整數(shù),拋擲這個(gè)正十二面體1次。
(1)朝上一面的數(shù)會(huì)有哪些?它們發(fā)生的可能性相同嗎?
(2)朝上一面的數(shù)是奇數(shù)與朝上一面的數(shù)是偶數(shù),發(fā)生的可能性相同嗎?
(3)朝上一面的數(shù)是4的倍數(shù)與朝上一面的數(shù)是6的倍數(shù),發(fā)生的可能性相同嗎?積極動(dòng)腦,找尋情境間的內(nèi)在聯(lián)系,主動(dòng)建構(gòu)知識(shí)體系. 再度體驗(yàn)問題情境,感悟模型之間的內(nèi)在聯(lián)系。積
極動(dòng)腦,找尋情境間的內(nèi)在聯(lián)系,主動(dòng)建構(gòu)知識(shí)體系。
再度體驗(yàn)問題情境,感悟模型之間的內(nèi)在聯(lián)系。
課堂小結(jié)
通過這節(jié)課你學(xué)到了什么?你還想進(jìn)一步研究什么?對(duì)所
學(xué)知識(shí)進(jìn)行反思、歸納和總結(jié)。讓學(xué)生對(duì)知識(shí)進(jìn)行提煉,體會(huì)數(shù)學(xué)知識(shí)的應(yīng)用,將感性的認(rèn)識(shí)升華為理性的認(rèn)識(shí)。
作業(yè)布置
同步練習(xí)4.1等可能性。獨(dú)立完成。了解教學(xué)效果,及時(shí)調(diào)整教學(xué)內(nèi)容和方法。
案例反思
奧蘇貝爾說過:“如果我不得不把全部教育心理學(xué)還原為一條原理的話,我將會(huì)說,影響學(xué)習(xí)最重要的是學(xué)生已經(jīng)知道了什么。原有的學(xué)習(xí)對(duì)新的學(xué)習(xí)的影響,就是已有的認(rèn)知結(jié)構(gòu)對(duì)新的學(xué)習(xí)的影響,這也就是心理學(xué)上所說的遷移。”在數(shù)學(xué)教學(xué)中,要通過知識(shí)對(duì)比,尋找知識(shí)間的內(nèi)在聯(lián)系,探求它們的共同特點(diǎn)、共同原理、共同規(guī)律,進(jìn)行知識(shí)梳理,然后運(yùn)用這些特點(diǎn)、原理、規(guī)律指導(dǎo)學(xué)生去學(xué)習(xí)新的知識(shí),達(dá)到“一把鑰匙打開多把鎖”的目的;同時(shí)抓好對(duì)數(shù)學(xué)核心內(nèi)容、基本能力、基本技能和基本思想方法的教學(xué),加強(qiáng)課內(nèi)到課外的延伸,對(duì)學(xué)得的知識(shí)和技能的重組和拓展,實(shí)現(xiàn)知識(shí)的橫向遷移,“舉一反三,觸類旁通”,從而培養(yǎng)學(xué)生的知識(shí)遷移能力。
課堂教學(xué)是實(shí)施數(shù)學(xué)新課程的主陣地。培養(yǎng)學(xué)生數(shù)學(xué)知識(shí)的遷移類推能力,當(dāng)然也離不開這個(gè)主陣地。因此,必須切實(shí)轉(zhuǎn)變教學(xué)方式,在優(yōu)化數(shù)學(xué)課堂教學(xué)上狠下功夫,特別要通過抓好數(shù)學(xué)課堂教學(xué)各個(gè)環(huán)節(jié),促進(jìn)學(xué)生數(shù)學(xué)知識(shí)遷移類推能力的培養(yǎng)。
《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)》把“能通過觀察、實(shí)驗(yàn)、歸納、類比等獲得數(shù)學(xué)猜想”作為推理能力的一種表現(xiàn)。類比是一種相似,它是從一種特殊到另一種特殊的推理,實(shí)現(xiàn)從具體到抽象。從舊知識(shí)到新知識(shí)、從已知領(lǐng)域到未知領(lǐng)域的遷移過程,這個(gè)過程要經(jīng)過分析、類比、猜想得出新結(jié)論,這就是創(chuàng)新的過程,數(shù)學(xué)知識(shí)的遷移過程。知識(shí)掌握是知識(shí)運(yùn)用的前提,知識(shí)應(yīng)用是知識(shí)掌握的歸宿。知識(shí)掌握是學(xué)習(xí)者單向的內(nèi)化建構(gòu),而知識(shí)運(yùn)用是逆向外化于物。在日常數(shù)學(xué)教學(xué)中,教師要根據(jù)不同的教學(xué)內(nèi)容,采用不同的教學(xué)方法,以便有效地促進(jìn)知識(shí)的遷移。
要想在課堂中順利實(shí)現(xiàn)各知識(shí)點(diǎn)間的遷移,我們的數(shù)學(xué)課堂還應(yīng)該是民主的、自由的、活動(dòng)的。首先,民主是現(xiàn)代課程中的重要理念。民主最直接的體現(xiàn)是在課程實(shí)施中學(xué)生能夠平等地參與,只有被動(dòng)接受,就沒有民主可言。相反,如果沒有民主,學(xué)生的參與就不是主動(dòng)參與,而是被動(dòng)的、消極的。教師在課堂中應(yīng)該形成一種利于學(xué)生人際關(guān)系的氛圍。尊重每一個(gè)學(xué)生,只有尊重學(xué)生,才能理解學(xué)生,才能做到平等對(duì)待每一個(gè)學(xué)生,學(xué)生才會(huì)感到被尊重,才不會(huì)出現(xiàn)有的學(xué)生被冷落、被諷刺,甚至被恥笑的現(xiàn)象。
其次,教師在提問時(shí),應(yīng)該設(shè)計(jì)開放性的問題,讓每一個(gè)學(xué)生能有發(fā)揮的空間和時(shí)間,并給學(xué)生足夠的時(shí)間進(jìn)行思考、討論、探索,讓學(xué)生在這個(gè)空間和時(shí)間里可以按自己的方式展開想象,才能使他們暢所欲言,學(xué)有所獲。
最后,作為教師,我們不能忘記“十個(gè)手指有長短,學(xué)生的能力各不同”。我們要能及時(shí)發(fā)現(xiàn)“學(xué)困生”的閃亮之處,并能及時(shí)給予他們鼓勵(lì)和肯定,讓他們也能以積極的態(tài)度面對(duì)學(xué)習(xí)和生活中的各種問題。
更重要的是,在平時(shí)的訓(xùn)練中,教師首先要讓學(xué)生學(xué)會(huì)把零散知識(shí)變成結(jié)構(gòu)知識(shí),考查知識(shí)之間的相互聯(lián)系,分辨、歸類并總結(jié)同類知識(shí)的特點(diǎn)和內(nèi)在規(guī)律;其次是學(xué)會(huì)將考點(diǎn)知識(shí)變成題型知識(shí),考點(diǎn)知識(shí)是很抽象的,要具體通過題目才能得以體現(xiàn);最后就是學(xué)會(huì)把缺漏知識(shí)變新增知識(shí),把殘缺知識(shí)變成系統(tǒng)知識(shí),也就是查缺補(bǔ)漏,綜合運(yùn)用。這些是知識(shí)遷移的基石,通過長期的不斷訓(xùn)練,就能提高他們的思維水平,提高他們數(shù)學(xué)知識(shí)的遷移能力。
參考文獻(xiàn):
黃浩活.試論中學(xué)數(shù)學(xué)教學(xué)中的負(fù)遷移[J].中學(xué)教學(xué)參考,2015.

