基于Hilbert-Huang變換的列車車輪失圓故障診斷

李奕璠， 劉建新， 李忠繼

(1.西南交通大學(xué)機(jī)械工程學(xué)院 成都， 610031) (2.西南交通大學(xué)牽引動力國家重點(diǎn)實(shí)驗(yàn)室 成都， 610031) (3.中鐵二院工程集團(tuán)有限責(zé)任公司科學(xué)技術(shù)研究院 成都， 610031)

?

基于Hilbert-Huang變換的列車車輪失圓故障診斷

李奕璠1， 劉建新2， 李忠繼3

(1.西南交通大學(xué)機(jī)械工程學(xué)院 成都， 610031) (2.西南交通大學(xué)牽引動力國家重點(diǎn)實(shí)驗(yàn)室 成都， 610031) (3.中鐵二院工程集團(tuán)有限責(zé)任公司科學(xué)技術(shù)研究院 成都， 610031)

研究列車車輪失圓的檢測與診斷問題，采用基于改進(jìn)的希爾伯特-黃變換(Hilbert-Huang transform, 簡稱HHT)的處理方法，首先，針對HHT方法固有的模態(tài)混疊現(xiàn)象，提出一種形態(tài)濾波-能量原則算法；然后，建立車輛軌道耦合動力學(xué)模型和典型的車輪故障模型，計(jì)算軸箱垂向振動的動態(tài)響應(yīng)；最后，運(yùn)用改進(jìn)的HHT分析方法提取正常車輪、多邊形化車輪和擦傷車輪引起的軸箱垂向振動的特征。研究結(jié)果表明，正常車輪與故障車輪之間以及不同類型故障的車輪之間Hilbert譜差異顯著，可見該方法能夠有效診斷車輪失圓故障。

車輪多邊形； 踏面擦傷； 希爾伯特-黃變換； 模態(tài)混疊

引 言

隨著列車運(yùn)行速度的提高，輪軌相互作用力增強(qiáng)，輪軌間的磨耗及接觸疲勞愈發(fā)嚴(yán)重，車輪失圓現(xiàn)象難以避免。失圓車輪運(yùn)行時會產(chǎn)生沖擊，引起整個車輛軌道系統(tǒng)耦合振動，降低乘坐舒適度，損壞線路及車輛部件，甚至危及行車安全。因此，對車輪狀態(tài)進(jìn)行實(shí)時檢測與診斷很有必要。車輪振動信息受諸多因素的影響，故障特征提取的準(zhǔn)確性與可靠性一直是一個難點(diǎn)問題。

車輪失圓是指車輪踏面型面的變化，可分為局部失圓和全周失圓兩大類。踏面剝離和踏面突起等屬于典型的局部失圓現(xiàn)象。全周失圓主要指車輪多邊形化。國內(nèi)外學(xué)者針對車輪失圓的診斷進(jìn)行了大量研究。測試輪軌垂向力是判斷車輪狀態(tài)最普遍采用的方法[1-2]，然而在軌道上布置應(yīng)變片的數(shù)量畢竟有限，車輪缺陷部位恰好作用在傳感器安裝點(diǎn)的概率較小，容易漏判。由于振動的響應(yīng)范圍更大，因此文獻(xiàn)[3]在軌道安裝加速度傳感器，通過測量軌道的振動來推測車輪狀態(tài)，但該方法難以避免鄰輪可能帶來的干擾。此外，光學(xué)[4]、超聲波[5]、機(jī)械[6]系統(tǒng)也被用于車輪失圓的檢測中，但這些系統(tǒng)僅能在靜態(tài)或低速時使用。以上方法的共同缺陷在于將檢測系統(tǒng)放置在軌道上或軌道附近，無法對車輛運(yùn)行狀態(tài)進(jìn)行全過程檢測。如果將傳感器安裝在車輛上，就能克服此不足。由車輪故障引起的車輛異常振動能在軸箱直接體現(xiàn)，Molodova等[7]利用軸箱垂向振動加速度識別軌道缺陷。

筆者研究了一種利用軸箱振動加速度信號實(shí)現(xiàn)對車輪失圓進(jìn)行診斷的方法，運(yùn)用改進(jìn)的HHT方法提取軸箱振動的時頻特征。

1 HHT理論

HHT是一種非平穩(wěn)信號分析方法[8]，包括經(jīng)驗(yàn)?zāi)B(tài)分解(empirical mode decomposition，簡稱EMD)和Hilbert變換兩部分。該方法首先采用EMD將信號自適應(yīng)地分解成若干個固有模態(tài)函數(shù)(intrinsic mode function, 簡稱IMF)，然后對每個IMF分量進(jìn)行Hilbert變換，得到瞬時頻率和瞬時幅值，進(jìn)而得到Hilbert譜。由于HHT良好的時頻分辨率及自適應(yīng)性，該方法得到了廣泛應(yīng)用，但模態(tài)混疊是影響HHT的主要問題，該方法仍需完善。

2 模態(tài)混疊

EMD的本質(zhì)是對信號的特征尺度進(jìn)行篩分，得到的IMF是頻率從高到低的有序排列，每一個IMF分量分別對應(yīng)原信號中不同尺度的局部特征。當(dāng)原信號中混有間斷事件、脈沖干擾或噪聲時(統(tǒng)稱為異常事件)，IMF分量會產(chǎn)生模態(tài)混疊現(xiàn)象。模態(tài)混疊是指在一個IMF中包含差異較大的特征尺度，或相近的特征尺度分布在不同的IMF中，使IMF分量失去物理意義。目前，處理模態(tài)混疊問題的方法根據(jù)其原理，大致可分為3類：異常事件消除法[9]、輔助信號添加法[10-11]和信號濾波法[12-13]，這些方法都存在各自的問題。筆者提出了一種結(jié)合形態(tài)學(xué)濾波與能量原則的方法處理模態(tài)混疊問題。

2.1 形態(tài)學(xué)濾波

形態(tài)學(xué)濾波是基于數(shù)學(xué)形態(tài)學(xué)變換的非線性濾波方法，它依據(jù)待處理信號的局部形態(tài)特征，通過數(shù)學(xué)形態(tài)學(xué)變換，將信號與噪聲分離。形態(tài)濾波的基本思想是設(shè)計(jì)一個稱作結(jié)構(gòu)元素的“探針”，通過探針的移動，對信號進(jìn)行匹配，達(dá)到提取信號、保持細(xì)節(jié)和抑制噪聲的目的。

2.2 能量原則

信號x(t) 經(jīng)EMD分解后，得到n-1個IMF分量 c(t)和一個余項(xiàng)r(t)，即

(1)

由EMD的完備性與正交性可知

(2)

若分解得到的某一分量di(t)不是正交分量，那么當(dāng)di(t)分離出去后，信號的總能量Et變?yōu)?/p>

(3)

不失一般性，令

(4)

其中：ei(t)為非正交的誤差成分。

式(3)可表示為

(5)

由式(5)可知，對信號進(jìn)行EMD分解后，如果分解結(jié)果是原始信號的固有模態(tài)分量，則分解前后信號總能量不會發(fā)生變化，此時e(t)=0，Et=Ex。如果分解得到的部分分量不是正交分量，EMD分解不服從能量守恒原理，分解后能量增加，有Et>Ex。

EMD可表示為

(6)

其中：cj(t)為真實(shí)模態(tài)分量；fk(t)為虛假模態(tài)分量。

所有IMF分量的和包含了原始信號與分解誤差[14]

(7)

由式(6)和式(7)可得

(8)

式(8)表明，EMD分解誤差與虛假模態(tài)分量大小相等。

根據(jù)以上分析，筆者提出一種檢測和去除虛假模態(tài)分量的方法，具體步驟如下。

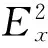
2) 將分解得到的每一個分量分別與原信號進(jìn)行相關(guān)分析，將相關(guān)系數(shù)最大的分量ci(t)確定為真實(shí)模態(tài)分量。

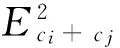
4) 用原信號減去所有虛假模態(tài)分量，再進(jìn)行EMD，若分解結(jié)果滿足精度要求，停止；否則回到步驟1。

2.3 算法驗(yàn)證

采用仿真信號x(t)=x1(t)+x2(t)+x3(t)對提出的方法進(jìn)行驗(yàn)證，其中：x1(t)為兩個諧波信號的和，x1(t)=sin(2πt)+cos(4πt)；x2(t)為脈沖干擾；x3(t)為高斯噪聲；信噪比為16 dB；采樣頻率為100 Hz。仿真信號的時間歷程曲線如圖1所示。

使用EMD對該信號進(jìn)行分解，分解結(jié)果出現(xiàn)了模態(tài)混疊現(xiàn)象，IMF分量無法對應(yīng)仿真信號中1 Hz與2 Hz的頻率成分，限于篇幅，不再給出此結(jié)果。為了抑制模態(tài)混疊，在EMD的基礎(chǔ)上，文獻(xiàn)[10]提出了總體平均經(jīng)驗(yàn)?zāi)B(tài)分解(ensemble empirical mode decomposition, 簡稱EEMD)方法。仿真信號的EEMD結(jié)果如圖2所示。所添加的白噪聲的幅值為信號標(biāo)準(zhǔn)差的0.001 3倍，總體平均次數(shù)為100次。可見，模態(tài)混疊現(xiàn)象得到了抑制。圖2中的IMF4和IMF5分量分別對應(yīng)2 Hz與1 Hz的諧波信號。

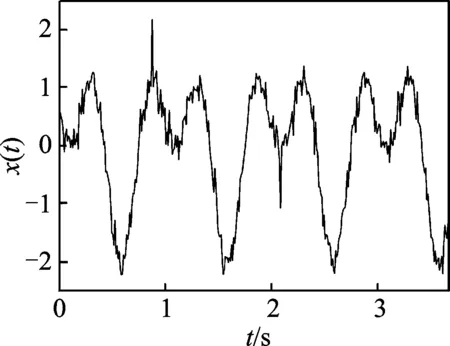
圖1 仿真信號Fig.1 Simulated signal

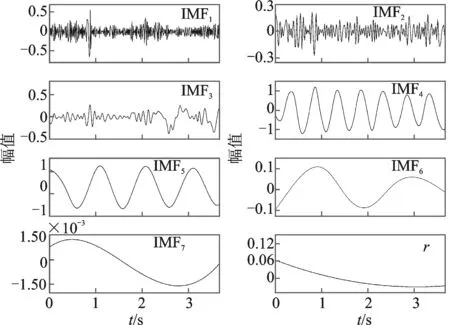
圖2 EEMD分解結(jié)果Fig.2 Results of EEMD

對圖1所示的仿真信號進(jìn)行形態(tài)濾波，選擇半圓形結(jié)構(gòu)元素，結(jié)構(gòu)元素的長度為9個采樣點(diǎn)，半徑為0.05。利用形態(tài)濾波-能量原則算法，經(jīng)一次循環(huán)后結(jié)果如圖3所示。可以看到，仿真信號的兩個諧波成分被分解到IMF3和IMF4，其中，IMF3代表2Hz余弦信號，IMF4代表1Hz正弦信號。

為了評價形態(tài)濾波-能量原則算法的效果，將圖3與圖2進(jìn)行比較發(fā)現(xiàn)，圖3中無意義的虛假成分較圖2減少。分別計(jì)算每種方法的分解結(jié)果與真實(shí)信號間的均方誤差。表1為兩種方法的計(jì)算結(jié)果精度比較，這里只計(jì)算了有意義的IMF分量(圖2的IMF4和IMF5，圖3的IMF3和IMF4)。可見，形態(tài)濾波-能量原則算法不僅能夠有效抑制模態(tài)混疊，還具有更好的時間分辨率。這只是算法經(jīng)一次循環(huán)得到的結(jié)果，若循環(huán)次數(shù)增加，精度還有一定的提升空間。

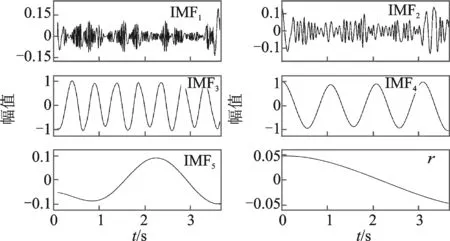
圖3 形態(tài)濾波-能量原則算法處理結(jié)果Fig.3 Results of morphology filtering and energy principle algorithm

方法IMF3IMF4IMF5EEMD—9.27486.7921形態(tài)濾波-能量原則算法4.79704.7130—

3 仿真分析

參見文獻(xiàn)[15]建立車輛軌道耦合動力學(xué)模型。車輪失圓的具體表現(xiàn)形式多樣，筆者選取車輪踏面擦傷和車輪多邊形化兩種典型狀態(tài)進(jìn)行分析。

3.1 正常車輪

計(jì)算無故障車輪的車輛以200 km/h運(yùn)行時的軸箱垂向振動響應(yīng)，其時間歷程和對應(yīng)的Hilbert譜如圖4所示。正常狀態(tài)下，軸箱垂向振動信號的Hilbert譜在時頻域呈均勻分布，沒有明顯的特征。

3.2 踏面擦傷車輪

計(jì)算了兩種工況下軸箱垂向振動響應(yīng)。工況1：車輪擦傷長度為10 mm，車速為100 km/h，無軌道激擾。工況2：車輪擦傷長度為10 mm，車速為100 km/h，軌道激擾為美國五級譜。兩種工況下的時間歷程曲線及其Hilbert譜如圖5，6所示。可以看出，當(dāng)車輪滾動到擦傷位置時，對應(yīng)的Hilbert譜在垂向上呈條帶狀分布，相鄰兩個條帶的寬度相等，為兩次沖擊的時間間隔，即車輪滾動一周所用的時間。因此，可以根據(jù)該特征對存在踏面擦傷的車輪進(jìn)行識別。

為了驗(yàn)證本研究方法的有效性，將該方法對工況2信號的處理結(jié)果與使用FFT和傳統(tǒng)的HHT方法進(jìn)行比較。圖7為圖6(a)所示信號的FFT分析結(jié)果，從頻譜圖中難以發(fā)現(xiàn)擦傷引起的故障特征。振動主要集中在100 Hz以下的范圍內(nèi)，而這也是圖5, 6中Hilbert譜分析頻率設(shè)定為0～100 Hz的原因。傳統(tǒng)的HHT方法的分析結(jié)果如圖8所示，可以大致看到幾個垂向條帶，干擾非常明顯。與圖6(b)相比，部分故障特征被掩蓋，這是由EMD分解時模態(tài)混疊現(xiàn)象引起的。

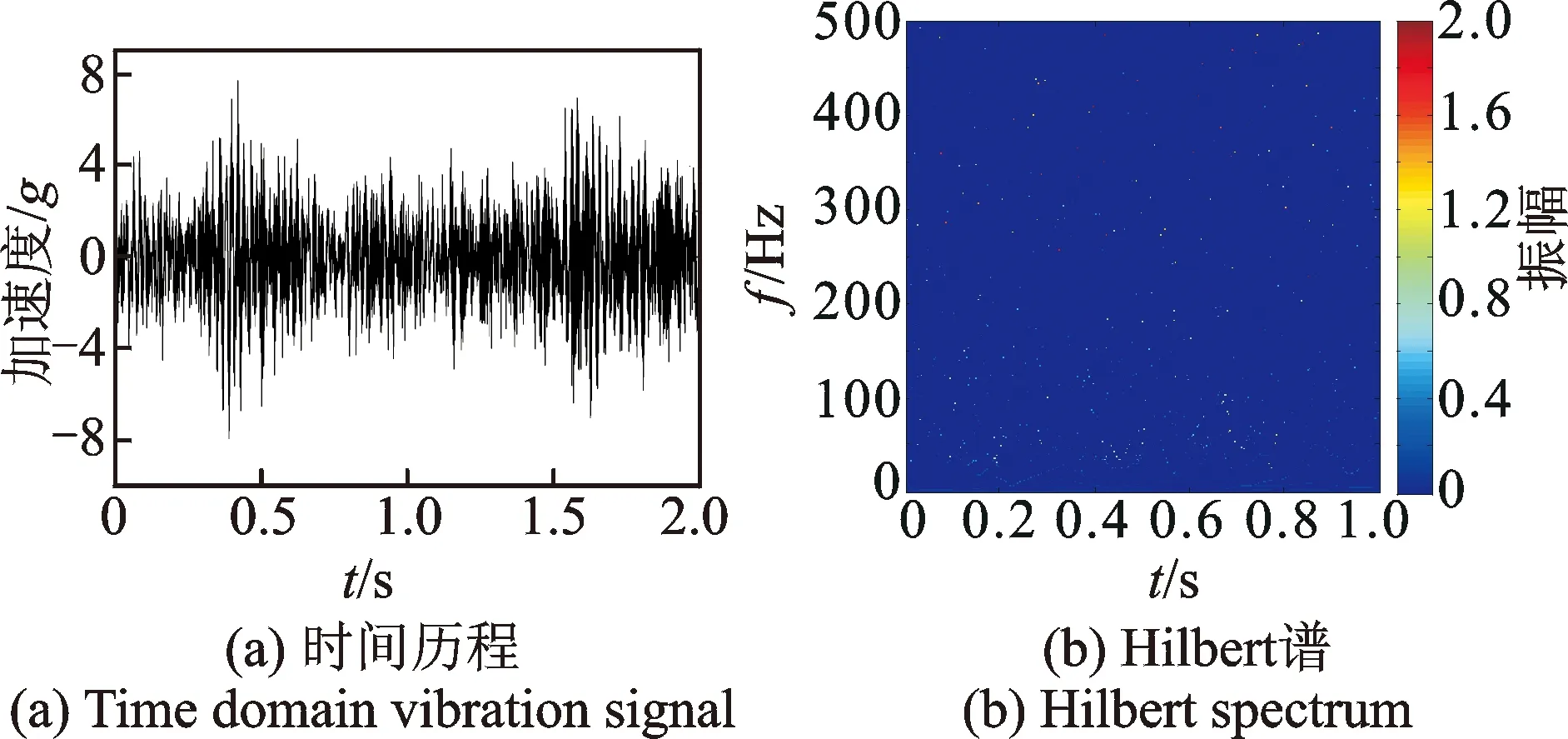
圖4 車輪無故障狀態(tài)下軸箱加速度的時間歷程及Hilbert譜Fig.4 Time history and Hilbert spectrum of axle-box acceleration with healthy wheels

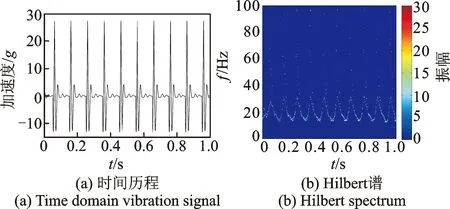
圖5 工況1的軸箱加速度時間歷程及其Hilbert譜Fig.5 Time history and Hilbert spectrum of axle-box acceleration in case 1

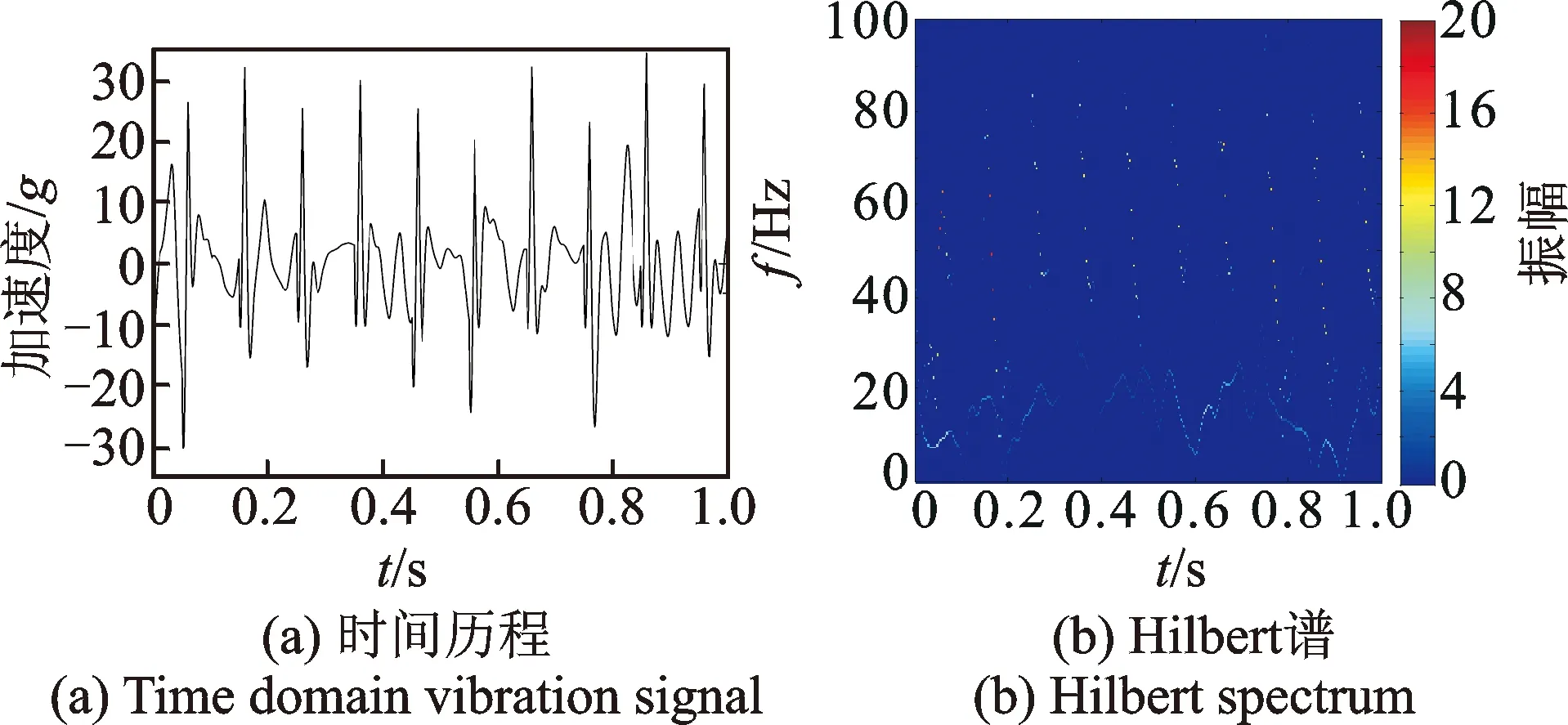
圖6 工況2的軸箱加速度時間歷程及其Hilbert譜Fig.6 Time history and Hilbert spectrum of axle-box acceleration in case 2

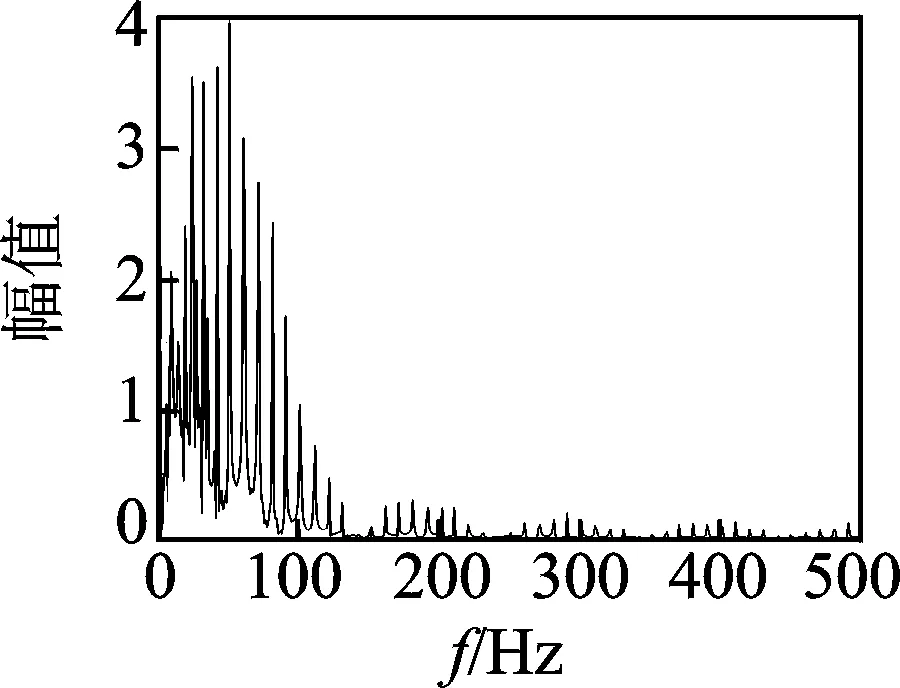
圖7 FFT的分析結(jié)果
Fig.7 Results of FFT

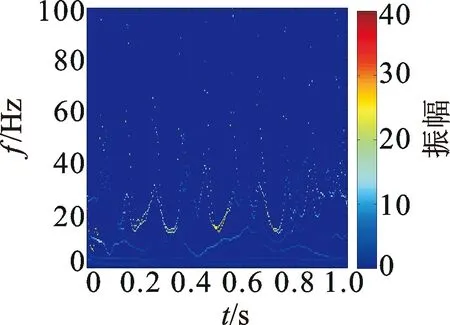
圖8 傳統(tǒng)HHT方法的分析結(jié)果
Fig.8 Results of traditional HHT

3.2.1 軌道不平順的影響

不同的線路條件會使得車輛的振動響應(yīng)各異，軸箱振動信號的幅值和頻率同樣會隨之改變，干擾車輪踏面擦傷的檢測與診斷。為了分析不同的軌道激擾對本研究方法的影響，選用美國三級譜不平順作為軌道激勵進(jìn)行仿真計(jì)算，其他參數(shù)與工況2相同。

圖9為此工況下軸箱垂向振動加速度信號的時間歷程曲線及其頻譜。對比圖9和圖6的時域信號可知，選用的美國三級譜線路的狀態(tài)比美國五級譜要差，此不平順作用下列車振動更劇烈，車輪擦傷引起的沖擊幾乎被淹沒。經(jīng)本研究方法處理后得到的Hilbert譜在垂向上呈條帶狀分布，說明車輪存在踏面擦傷故障，體現(xiàn)了形態(tài)濾波-能量原則算法抑制噪聲、提取沖擊的能力。從圖9可見，即使在線路條件不理想的狀態(tài)下，本研究方法依然能識別出車輪故障。

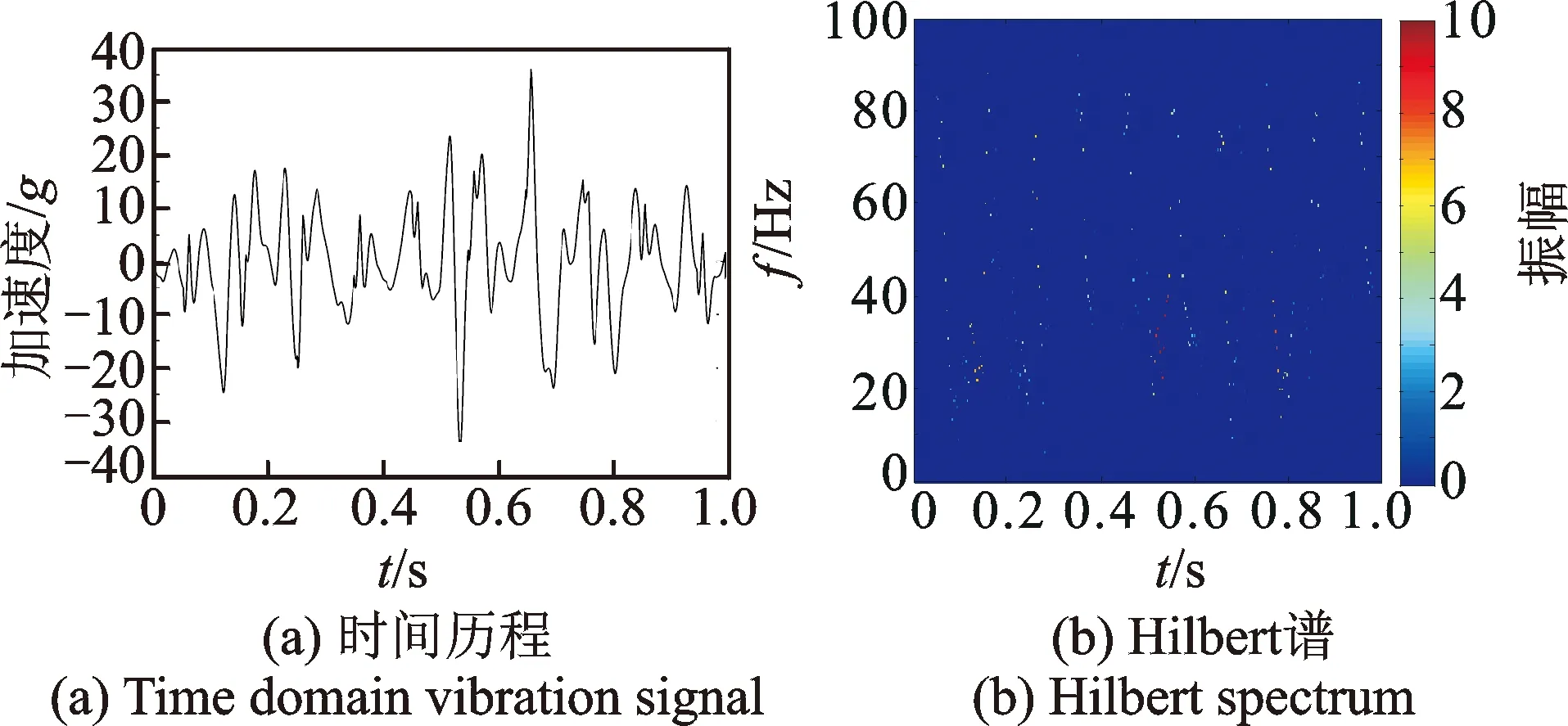
圖9 軌道不平順的影響Fig.9 The influence of track irregularity

3.2.2 車速的影響

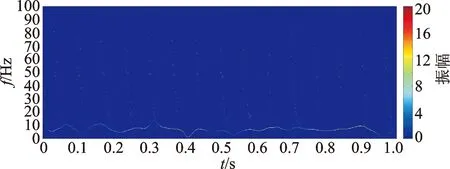
圖10 車速的影響Fig.10 The influence of speed

車輛運(yùn)行速度變化同樣會使軸箱振動信號發(fā)生改變，并影響車輪擦傷沖擊的幅值和頻率。為了分析車輛運(yùn)行速度的變化對檢測和診斷能力的影響，計(jì)算了車輛以150 km/h運(yùn)行時的軸箱垂向加速度響應(yīng)，其他參數(shù)與工況2一致。由于車速發(fā)生了改變，相應(yīng)的故障頻率變?yōu)?5 Hz。圖10為此工況下的Hilbert譜，從圖中可以清晰地看到15個均勻間隔的垂向條帶，從而有效地識別出車輛踏面擦傷故障。在行車速度發(fā)生改變的情況下，本研究方法能較為準(zhǔn)確地跟蹤變化趨勢，確保故障特征的有效識別，體現(xiàn)了診斷方法的魯棒性。

3.3 多邊形車輪

計(jì)算了具有一階和二階多邊形化車輪的車輛以300 km/h的速度運(yùn)行時的軸箱垂向加速度，對其進(jìn)行Hilbert譜分析，如圖11所示。可以看到，多邊形車輪引起的軸箱垂向振動的Hilbert譜在橫向上呈條帶狀分布，不同階次的多邊形車輪對應(yīng)不同的特征頻率，這與正常狀態(tài)下的Hilbert譜差異顯著，且與擦傷車輪所致軸箱振動的Hilbert譜的特征完全不同。圖11(a)中，一階多邊形化車輪引起的軸箱垂向振動的Hilbert譜在30 Hz附近出現(xiàn)了清晰的橫向條帶。在仿真計(jì)算中，車輪周長為2.89 m，車輪轉(zhuǎn)動的頻率為28.8 Hz，偏心車輪在滾動一周的過程中會發(fā)生一次周期性變化，因此Hilbert譜的分析結(jié)果與理論相符。圖11(b)中，由于橢圓車輪在滾動一圈的過程中會發(fā)生兩次周期性變化，所以軸箱振動頻率為圖11(a)的2倍。可見，正常車輪不會引起軸箱的異常振動，其Hilbert譜在整個時頻域內(nèi)呈均勻分布，擦傷車輪使得軸箱振動信號的Hilbert譜在垂向上呈條帶狀分布，多邊形車輪使得軸箱振動信號的Hilbert譜在橫向上呈條帶狀分布。因此，本研究方法能有效提取軸箱垂向振動的特征，從而診斷車輪故障，并能判斷故障類型，同時可以在車輛運(yùn)行過程中進(jìn)行實(shí)時檢測。

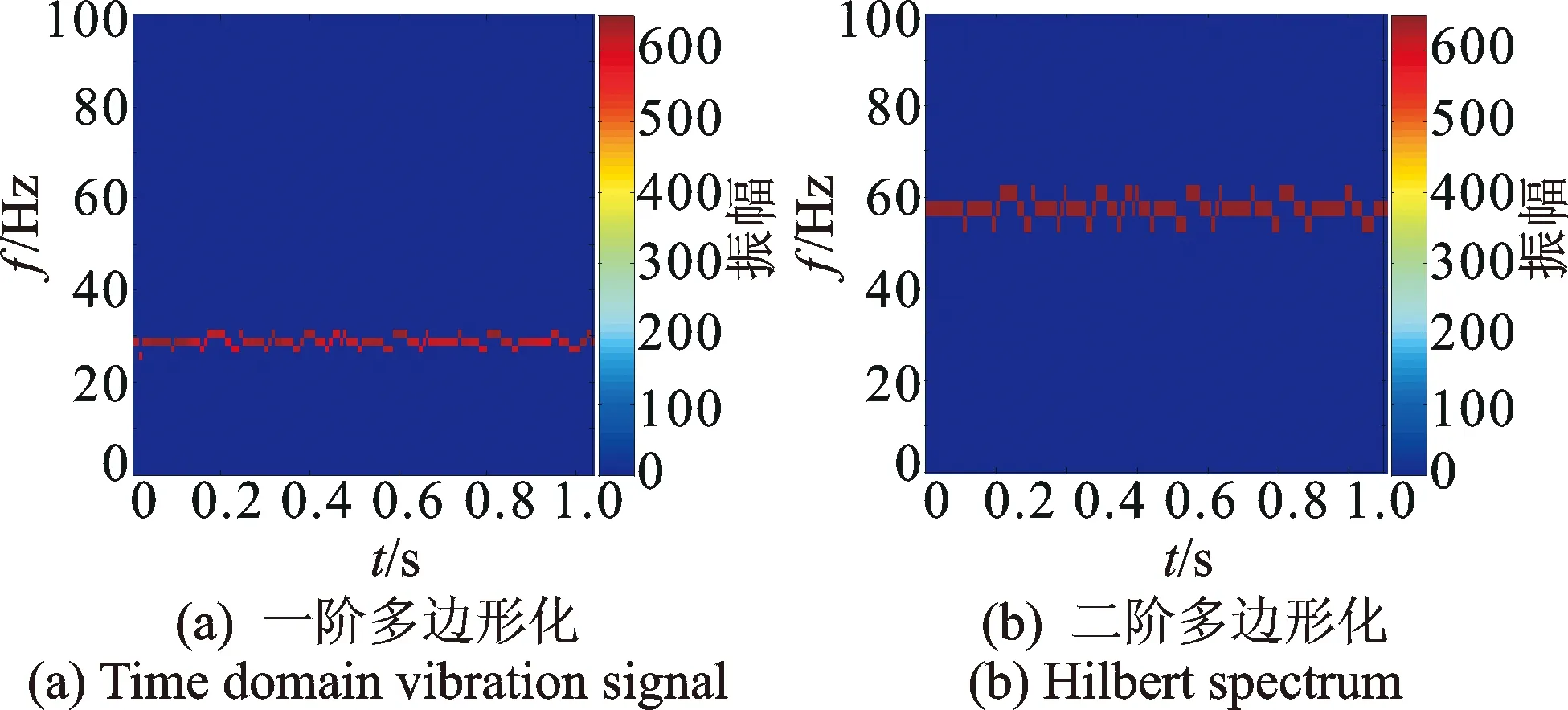
圖11 車輪多邊形化引起的軸箱垂向振動的Hilbert譜Fig.11 HHT spectrum of axle-box vibration caused by out-of-round wheels

4 實(shí)例分析

在滾動振動試驗(yàn)臺進(jìn)行了現(xiàn)場測試，試驗(yàn)車輛為某型動車組單節(jié)車輛。為了降低試驗(yàn)成本，在軌道輪接觸表面貼附膠塊來模擬車輪踏面擦傷時的情形。車輛運(yùn)行速度為200 km/h，軌道輪直徑為1.8 m，軌道激擾為國內(nèi)某既有線不平順。

圖12為現(xiàn)場測試獲得的軸箱垂向振動加速度，圖中很難發(fā)現(xiàn)太多有價值的信息。圖13為其頻譜分析結(jié)果，可以看到明顯的諧振頻響特征。由理論分析可知，車輪旋轉(zhuǎn)一周的過程中，輪軌間會產(chǎn)生一次劇烈沖擊，此時車輪的故障頻率等于其轉(zhuǎn)頻，約為9.8 Hz，但圖13中沒有出現(xiàn)此特征頻率，故頻譜分析方法的處理結(jié)果存在問題。本研究方法得到的Hilbert譜如圖14所示，圖中可以清晰分辨出垂向條紋，說明車輪存在踏面擦傷故障，條帶間隔約為0.1s，這正是車輪滾動一周所用的時間；同時在10 Hz附近出現(xiàn)了一橫向條紋，表明了此頻率故障的存在。

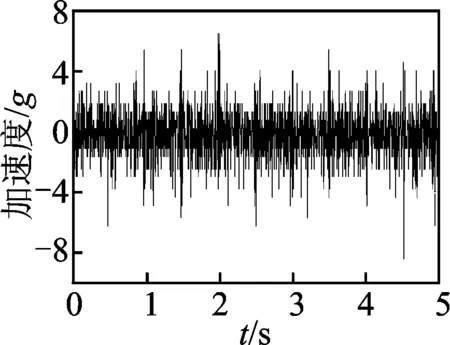
圖12 實(shí)測軸箱振動數(shù)據(jù)

Fig.12Measured data of axle-box vibration

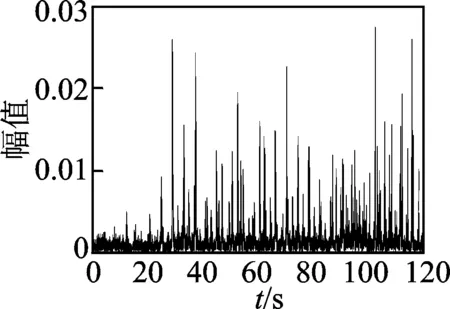
圖13 實(shí)測數(shù)據(jù)的FFT分析結(jié)果

Fig.13 FFT spectrum of measured data

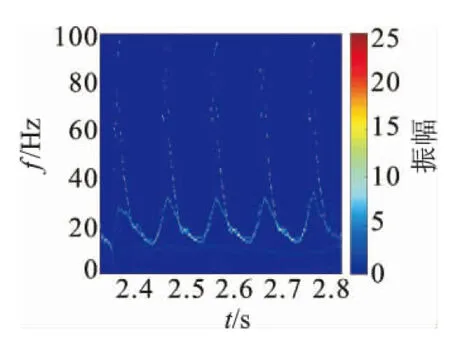
圖14 本研究方法得到的Hilbert譜Fig.14 Hilbert spectrum obtained by the method proposed in this paper

5 結(jié)束語

利用仿真和試驗(yàn)兩種手段，使用改進(jìn)的HHT方法對兩種常見的車輪失圓現(xiàn)象：車輪踏面擦傷及車輪多邊形化進(jìn)行研究。針對HHT方法存在的固有缺陷進(jìn)行改進(jìn)，提出形態(tài)濾波-能量原則算法處理模態(tài)混疊現(xiàn)象，并通過仿真信號證明了此方法的優(yōu)越性。利用改進(jìn)的HHT提取軸箱垂向振動信號的特征，取得了良好的效果，正常車輪的Hilbert譜呈均勻分布，擦傷車輪使得對應(yīng)的Hilbert譜在垂向上呈條帶狀分布，多邊形化車輪導(dǎo)致相應(yīng)的Hilbert譜在橫向上呈條帶狀分布，由此可對列車車輪狀態(tài)進(jìn)行有效地檢測與診斷。

[1] Milkovic D, Simic G, Jakovljevic Z. Wayside system for wheel-rail contact forces measurements[J]. Measurement, 2013, 46(9): 3308-3318.

[2] Filograno M L, Corredera P, Barrios A R, et al. Real time monitoring of railway traffic using fiber Bragg grating sensors[J]. Sensors Journal, 2012,12(1):85-92.

[3] Belotti V, Crenna F, Michelini R C, et al. Wheel-flat diagnostic tool via wavelet transform[J]. Mechanical System and Signal Processing, 2006, 20(8): 1953-1966.

[4] 敖銀輝，徐曉東，吳乃優(yōu). 用激光位移傳感器檢測輪對踏面缺陷[J]. 西南交通大學(xué)學(xué)報(bào)，2004，39(3): 345-348.

Ao Yinhui, Xu Xiaodong, Wu Naiyou. Defect detecting of train wheelset tread surface with laser displacement sensor[J]. Journal of Southwest Jiaotong University, 2004, 39(3): 345-348. (in Chinese)

[5] Brizuela J, Fritsch C, Ibanez A. Railway wheel-flat detection and measurement by ultrasound[J]. Transportation Research Part C, 2011, 19(6): 975-984.

[6] 馮其波，趙雁，崔建英. 車輪踏面擦傷動態(tài)定量測量新方法[J]. 機(jī)械工程學(xué)報(bào), 2002, 38(2): 120-122.

Feng Qibo, Zhao Yan, Cui Jianying. New dynamic method to quantitatively measure wheel flats or trains[J]. Chinese Journal of Mechanical Engineering, 2002, 38(2): 120-122. (in Chinese)

[7] Molodova M, Li Z, Dollevoet R. Axle box acceleration: measurement and simulation for detection of short track defects[J]. Wear, 2011, 271(1): 349-356.

[8] Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, 1998, 454(1971):903-995.

[9] Huang N E, Shen Z, Long S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457.

[10]Wu Z, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2005, 1(1):1-41.

[11]Shen W, Chen Y, Wu A. Low-complexity sinusoidal-assisted EMD (SAEMD) algorithms for solving mode-mixing problems in HHT[J]. Digital Signal Processing, 2014, 24: 170-186.

[12]Zarraga F L, Rios A L, Esquivel P, et al. A Hilbert-Huang based approach for on-line extraction of modal behavior from PMU data [C]∥North American Power Symposium. Starkville, USA: IEEE, 2009:1-6.

[13]秦品樂，林焰，陳明. 基于平移不變小波閾值算法的經(jīng)驗(yàn)?zāi)B(tài)分解方法[J]. 儀器儀表學(xué)報(bào), 2008, 29(12)：2637-2641.

Qin Pinle, Lin Yan, Chen Ming. Empirical mode decomposition method based on wavelet with translation invariance algorithm[J]. Chinese Journal of Scientific Instrument, 2008, 29(12): 2637-2641. (in Chinese)

[14]黃迪山. 經(jīng)驗(yàn)?zāi)B(tài)分解中虛假模態(tài)分量消除法[J]. 振動、測試與診斷, 2011, 31(3): 381-384.

Huang Dishan. Effect of sampling on empirical mode decomposition and correction[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3): 381-384. (in Chinese)

[15]李忠繼，魏來，戴煥云，等. 基于Hilbert-Huang變換的車輪扁疤識別方法[J].交通運(yùn)輸工程學(xué)報(bào)，2012，12(4): 33-41.

Li Zhongji, Wei Lai, Dai Huanyun, et al. Identification method of wheel flat based on Hilbert-Huang transform[J]. Journal of Traffic and Transportation Engineering, 2012, 12(4): 33-41. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.04.019

國家自然科學(xué)基金資助項(xiàng)目(51375403);中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金資助項(xiàng)目(SWJTU2682014BR001EM)

2014-10-08；

2014-12-30

U211.5； TH17

李奕璠，男，1985年4月生，講師。主要研究方向?yàn)闄C(jī)械設(shè)備安全監(jiān)測、故障診斷技術(shù)及信號處理。曾發(fā)表《測力鋼軌輪軌力解耦研究》(《機(jī)械工程學(xué)報(bào)》2013年第49卷第4期)等論文。

E-mail: li_yifan@foxmail.com