殊途同歸,巧求面積最值
柏黎平
殊途同歸,巧求面積最值
柏黎平

分析各地中考試卷,可以發現不少以二次函數知識為背景的壓軸題.二次函數在初中數學學習中占有重要地位,因其可以涵蓋初中數學的所有知識點,具有較強的綜合性,所以廣受各地中考命題人員的青睞.
二次函數壓軸題能考查綜合運用知識的能力,具有知識點多、條件隱蔽、關系復雜、思路難覓、解法靈活等特點,因此是中考數學的難點.不過,如果我們能在做習題的基礎上多總結一些方法,發現一些規律,有些難點就能較快突破.下面我們就一類二次函數與三角形面積的最值問題,來探求其中方法與規律.
一、規律發現
引例已知二次函數y=-x2+2x+3與x軸交于A、B兩點(A左B右),與y軸交于點C,連接BC,點P為直線BC上方拋物線上一動點,求△PBC面積的最大值及此時點P的坐標.

圖1

圖2
【解析】本題為求三角形面積最值問題,可以采用平行線法或構造二次函數模型求最值等兩種思路來解決問題.
解法1:如圖1,易求直線BC的解析式為:y=-x+3,所以可設直線l為y=-x+b.過點P作直線l∥BC,則多數情況下,直線l與拋物線有兩個交點,此時S△PBC顯然不是最大;當直線l與拋物線有唯一交點(即方程有唯一解)時,點P到BC的距離最大,因此S△PBC最大.①代入②化為一元二次方程可得x2-3x+ b-3=0,當Δ=0時,方程有兩個相等實數根,即.將b的值代回原方程組,可得此時點P的坐標為,再由P、B、C點坐標可求得△PBC的面積最大值為
解法2:如圖2,同樣求得直線BC的解析式為:y=-x+3.過點P作直線垂直于x軸,交直線BC于點D.
因為點P在拋物線上,所以可設點P坐標為(n,-n2+2n+3)(0≤n≤3),點D在BC上,因此坐標為(n,-n+3);以PD為底邊,設△PDC的高為h1,設△PDB的高為h2,則h1+h2=3,PD=(-n2+2n+3)-(-n+3)=-n2+3n.


這樣,S△PBC就是關于n的二次函數,根據二次函數性質易得當時,S△PBC的最大值,此時點P坐標為
【發現1】在解法1中,當三角形面積取得最大值時,只存在一個△PBC,但當面積縮小時,可能同時存在兩個不同的△PBC;
【發現2】在解法2中,將△PBC進行縱向切割,將其分割為兩個底邊都為PD的三角形,它們的高的和就是BC兩點的橫坐標的差;
【發現3】注意觀察兩種解法中,當三角形面積取得最大值時,點P的橫坐標是,而點C的橫坐標為0,點B的橫坐標為3,可以理解為點P的橫坐標恰好是線段BC中點的橫坐標.其實這種情況并不是巧合,是一種規律,是可以用數學方法證明的.(有興趣的同學可以拋物線y=ax2+bx+c和直線y=mx+n(am≠0)的交點是(x1,y1),(x2,y2)為一般情況進行證明,這里就不贅述.)
二、試刀中考
例1(2016·江蘇蘇州)如圖3,直線l∶y=-3x+3與x軸、y軸分別相交于A、B兩點,拋物線y=ax2-2ax+a+4(a<0)經過點B.
(1)求該拋物線的函數表達式;
(2)已知點M是拋物線上的一個動點,并且點M在第一象限內,連接AM、BM,設點M的橫坐標為m,△ABM的面積為S,求S與m的函數表達式,并求出S的最大值;
(3)略.

圖3

圖4
【解析】(1)方法略,函數解析式為:y=-x2+ 2x+3;
(2)本題初看與上面的引例不同,但其拋物線上的動點,及計算三角形面積的最值都與引例類似,可用解法2的方法求解問題,不過考慮到縱向作垂線分割三角形計算有一定的困難,可以采用橫向作垂線分割三角形,縱向距離為高.
如圖4,過點M作ME⊥y軸于點E,交AB于點D,可設點M坐標為(m,-m2+2m+3),D在AB上,因此D坐標為:
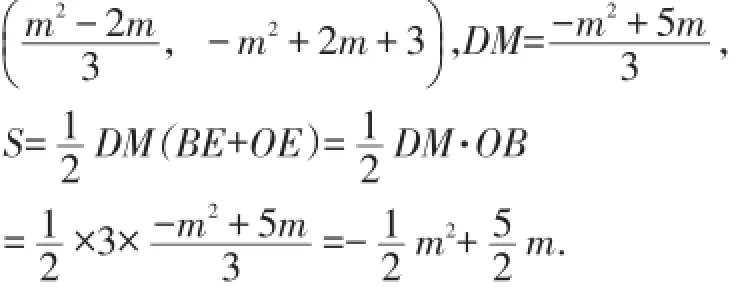
【評析】在平面直角坐標系中研究一些圖形的面積時,可采用割補法將復雜、不規則的圖形分割成若干個三角形計算.分割時要注意以下幾點:①分割后的三角形面積應該容易計算;②一般的分割方法為橫向或縱向;③如有必要,也可斜向分割.
如本題中也可連接OM,計算四邊形BOAM的面積減△BOA的面積.有時可能要進行多次嘗試,才能找到更為簡單的計算三角形面積的方法.
(1)點A的坐標為_______,點C的坐標為________;
(2)線段AC上是否存在點E,使得△EDC為等腰三角形?若存在,求出所有符合條件的點E的坐標;若不存在,請說明理由;
(3)點P為x軸上方的拋物線上的一個動點,連接PA、PC,若所得△PAC的面積為S,則S取何值時,相應的點P有且只有2個?

圖5

圖6
【解析】(1)解答略,A(0,4),C(8,0).
(2)易得D(3,0),CD=5.直線AC對應的解析式為,分三種情況討論:①DE= DC,②ED=EC,③CD=CE,可求得三個點E的坐標分別為:E1(0,4)
(3)本題思路較為難覓,關鍵要理解“S取何值時,相應的點P有且只有2個”這句話的意思:其實只要考慮S的取值范圍(即最大值與最小值),然后探討在S取不同數值時的點P的個數即可.在求S的取值范圍時,還要對點P所在的位置進行討論,當點P的位置在AC上方時,就可以用引例中的兩種方法求S的最大值,我們以第二種方法來解.
此時當且僅當S=16時,相應的點P只有1個,當0<S<16時,相應的點P有2個;
②點P在AB之間時,即-2<m<0時,易得S的最小值為0,最大值為20,且每個S的值都對應1個相應的點P.
故S=16時,相應的點P有且只有兩個.
【評析】本題的第(3)題問法比較難理解,尤其是“相應的點P有且只有2個”,這需要對此問題有一定的研究經驗,知道引例中的平行線研究方法的原理(關鍵是不同面積數值與點P的個數的對應關系),否則不容易聯想到要考慮△PAC面積的取值范圍.當然,在具體計算S的最大值時,還是用設坐標,用含m的代數式表示△PAC的面積的方法更為簡潔一些.
值得一提的是,如果我們能想到引例中“發現3”揭示的規律,甚至可以更為簡單地求出當點P在AC上方時S的最大值,即:當點P的橫坐標取點A(0,4)和點C(8,0)的中點(4,2)的橫坐標4時,△PAC的面積最大,于是可以迅速得出點P的坐標為(4,6),△PAC的面積就可以直接求,不必再用引例中的兩種稍嫌復雜的方法解答.可見,當我們做多了習題后,若能注重對同類型的問題進行一般性的總結,往往可以得出實用的規律,幫助我們簡化解題過程,從而節省計算的時間.
(作者單位:江蘇省太倉市雙鳳中學)

掃描二維碼,觀看名師微課

