運用探究歸納方法，發展學生推理能力——以蘇科版八（上）“探究三角形全等的條件1”為例

■謝建新

運用探究歸納方法，發展學生推理能力——以蘇科版八（上）“探究三角形全等的條件1”為例

■謝建新

推理能力是《義務教育數學課程標準（2011年版）》（以下簡稱《課標》）中提出的數學課程十個核心概念之一，其中，數學推理是指人們在數學觀念系統作用下，由若干數學條件，結合一定的數學知識、方法，對數學對象形成某種判斷的思維操作過程。《課標》指出推理能力的發展應貫穿于整個數學學習過程中。推理是數學的基本思維方式，也是人們學習和生活中經常使用的思維方式，一般包括合情推理和演繹推理，合情推理用于探索思路、發現結論，演繹推理用于證明結論。論證是推理形式的運用，推理是論證的工具。本文以發展學生推理能力為目的，與大家一起研討蘇科版八（上）“探究三角形全等的條件1”中的教學活動片段及設計意圖。

一、教學活動片段及設計意圖

教學活動1.復習引路，提出問題。

師：復習提問，什么叫全等三角形？

生1：兩個能夠完全重合的三角形叫做全等三角形。

師：如圖，△ABC與△DEF全等嗎？你是怎樣驗證的？

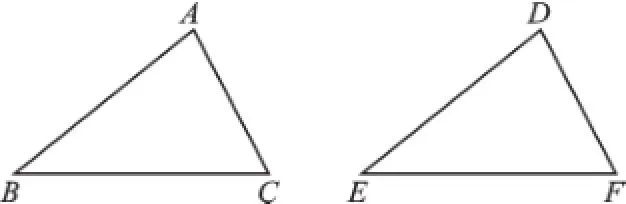
生2：用平移的方法看△ABC與△DEF是否完全重合，若完全重合，則全等；若不完全重合，則不全等。

師：也就是說，根據全等的定義來判斷兩個三角形全等，需要三條邊對應相等、三個角對應相等，即六個元素分別對應相等。是否有更簡單的判定方法呢？

（設計意圖：教師將前一節課內容進行復習，回憶什么叫做全等三角形，從中引出本節課的學習內容）

教學活動2.活動探究，發現問題。

師：根據全等的定義來判斷兩個三角形全等，需要三條邊對應相等、三個角對應相等，即六個元素分別對應相等。是否有更簡單的判定方法？例如：一個元素對應相等；兩個元素對應相等；三個元素對應相等……你是如何考慮的？

生3：可以從最簡單的情況開始考慮，看當兩個三角形一個元素分別相等時，一個角分別相等的兩個三角形是否全等，一條邊分別相等的兩個三角形是否全等。

生3：一個角分別相等的兩個三角形不全等。例如：我們手中天天用的這副三角板，每個三角板都有一個角為90°，而這兩塊三角板不重合，所以說，一個角分別相等的兩個三角形不全等。

生4：一條邊分別相等的兩個三角形也不全等。例如：我們手中天天用的這副三角板，等腰直角三角板的斜邊與另一塊直角三角板60°角所對的直角邊相等，而這兩塊三角板不重合，所以說，一條邊分別相等的兩個三角形不全等。

師：剛才兩位同學說得很好，請問：當兩個三角形兩個元素分別對應相等時又將怎樣？有幾種情況？

生5：當兩個三角形兩個元素分別相等時有三種類型：第一種，兩個角分別相等的兩個三角形是否全等；第二種，兩條邊分別相等的兩個三角形是否全等；第三種，一角一邊分別相等的兩個三角形是否全等。

生6：兩個角分別相等的兩個三角形不全等。例如，老師用的含30°、60°的直角三角板與我手中含30°、60°的直角三角板有兩個角分別相等，老師的三角板大而我的三角板小，不會完全重合，所以說，兩個角分別相等的兩個三角形不全等。

生7：一邊一角分別相等的兩個三角形不全等。例如，我們手中天天用的這副三角板，等腰直角三角板的斜邊與另一塊直角三角板60°角所對的直角邊相等，這兩塊三角板都有一個相等的角為90°，而這兩塊三角板不重合，所以說，一邊一角分別相等的兩個三角形不全等。

生8：兩條邊分別相等的兩個三角形不全等。例如，頂角為90°，腰長為6cm的等腰三角形與頂角為60°，腰長為6cm的等腰三角形不會完全重合，所以說，兩條邊分別相等的兩個三角形不全等。

師：同學們講得很好，并且有很清晰的分類思想，請問：當兩個三角形三個元素分別對應相等時又將怎樣？有幾種情況？

生9：當兩個三角形三個元素分別相等時可分四種類型：第一種，（三角）三個角分別相等的兩個三角形是否全等；第二種，（兩角一邊）兩角夾邊分別相等的兩個三角形是否全等，兩角一邊分別相等的兩個三角形是否全等；第三種，（一角兩邊）兩邊夾角分別相等的兩個三角形是否全等，兩邊一角分別相等的兩個三角形是否全等；第四種，（三邊）三條邊分別相等的兩個三角形是否全等。

生10：當兩個三角形三個元素分別相等時分六種類型：第一種，（角角角）三個角分別相等的兩個三角形是否全等；第二種，（邊邊邊）三條邊分別相等的兩個三角形是否全等；第三種，（角邊角）兩角夾邊分別相等的兩個三角形是否全等；第四種，（角角邊）兩角一邊分別相等的兩個三角形是否全等；第五種，（邊角邊）兩邊夾角分別相等的兩個三角形是否全等；第六種，（邊邊角）兩邊一角分別相等的兩個三角形是否全等。

（設計意圖：在《課標》中，明確提出了“學生應當有足夠的時間和空間經歷觀察、實驗、猜想、驗證、推理、計算、證明等活動過程”的要求。這就要求我們在課堂上應努力呈現有效的問題情境，以便學生能根據有效的情景展開合理猜想。在上面的教學中，教師能夠根據學生的實際，合情合理地引導學生大膽進行思考、推理、猜想得出結論）

教學活動3.動手操作，獲得事實。

師：本節課我們一起研究兩邊夾角分別相等的兩個三角形是否全等。

操作1：同學們把課前老師布置的作業——畫好的三角形拿出來（AB=5㎝，∠A=40°，AC=4㎝三角形），同學之間互相交流你有什么發現。

生11：我們所畫的三角形都一樣。

生12：我們畫的是一個特殊的三角形。如果畫一般的三角形會全等嗎？

師：該同學提出的問題很好，我們一起來思考。

操作2：對照課本第13頁，按下列作法，用直尺和圓規作△ABC，使∠A=∠α，AB=a，AC=b。

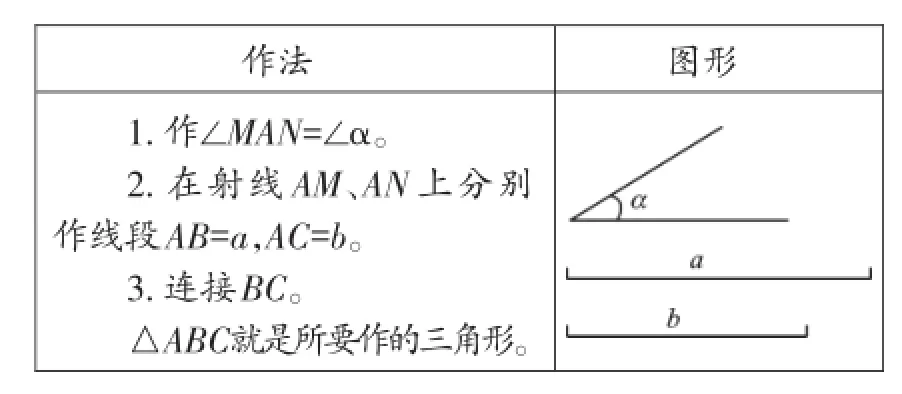
師：把你所作的三角形剪下來，與同組同學交流，有什么發現？

生13：老師，我們所作的三角形互相重合，即兩邊夾角分別相等的兩個三角形全等。

師：我們可以得到，判斷兩個三角形全等的一個基本事實：

兩邊及其夾角分別相等的兩個三角形全等（可以簡寫成“邊角邊”或“SAS”）。

（設計意圖：通過學生的動手操作、實驗、積極思考、合作交流等重要的學習方式得出實驗事實，學生經歷、體驗、探索活動得出的結論將終生難忘）

教學活動4.應用舉例，理解事實。

例：已知，如圖，AB=AD，∠BAC=∠DAC。

求證：△ABC≌△ADC。

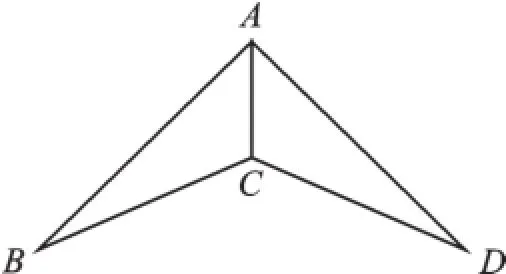
師：要證明△ABC≌△ADC，用什么判定方法？

生14：用剛學的“邊角邊”來判定這兩個三角形全等。

師：用“邊角邊”需要幾個條件？

生15：三個條件，兩條邊及其夾角分別相等，已知條件中已告訴我們一條邊一個角對應相等，只需找出另一條邊對應相等就行了。

師：另一條邊相等怎樣得到？

生16：我們把條件搬到圖形中，可以發現這兩個三角形還有一條公共邊即AC=AC，這樣三個條件就找到了。

證明：在△ABC和△ADC中

（設計意圖：例題出來后，先讓學生思考兩分鐘，教師提出問題，引導學生分析問題，發現解決問題的方法，同時提醒學生將已知條件搬到圖形上，發現圖中的隱含條件（公共邊相等），注意書寫格式，強調三角形全等邊角必須對應，進一步訓練學生的邏輯推理的規范性和思維的嚴密性。在例題中既體現了合情推理，也體現了演繹推理）

教學活動5.變式訓練，鞏固事實。

已知：如圖，AB=AC，點D、E分別在AB、AC上，且AD=AE。

求證：∠B=∠C。

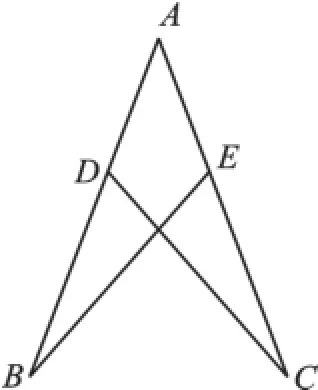
師：要證明∠B=∠C，應該想到什么？需要證明什么？

生17：該圖形可以看做△ABE與△ACD有一個公共角疊合在一起的兩個三角形，只要證明這兩個三角形全等就行了。

（設計意圖：本題的訓練目的是讓學生發現，將例題中的△ABC繞A點逆時針旋轉，∠BAC就變成了本題的圖形。進一步鞏固了幾何證明中演繹推理的書寫格式）

二、教學反思

1.教學設計應基于學情，培養學生的推理意識。

教學設計要基于學生的認知水平。《課標》中強調：數學教學活動必須建立在學生的認知發展水平和已有的知識經驗基礎之上。美國教育心理學家奧蘇伯爾說過：“影響學生學習的最重要的原因是學生已經知道了什么，我們應當根據學生原有的知識狀況進行教學。”上述課堂設計中，教師從學生已有的知識出發，把學生身邊常用的一副三角板拿出來多次作為教學中的反例，學生一目了然，讓知識自然生成，讓思維自由飛翔。把判斷兩個三角形全等的方法自然而然地引到三個條件對應相等的思路上來，可以說是水到渠成。學生的推理能力在已有的認知水平上不斷得到提升。

2.教學方法應尊重差異，發展學生的推理能力。

本節課以《課標》中課程核心概念為主線，在教學方法上尊重學生個體的認知差異，通過學生的動手操作、實驗、積極思考、合作交流發展學生的推理能力。

（1）在探究兩個三角形全等時，需找到幾個元素對應相等，先拋出問題引導學生從最簡單的情況開始思考，一個元素對應相等的兩個三角形不全等，兩個元素對應相等的兩個三角形不全等，學生能通過合情推理舉出反例，體現了學生的思想活動過程，通過經歷觀察、探究、合作交流的活動，充分發展了學生的合情推理能力。

（2）在獲得事實（兩邊及其夾角對應相等的兩個三角形全等）的過程中，學生通過尺規作圖作出相應的三角形，給學生充分的時間和空間經歷觀察、實驗、猜想、驗證、合作、推理獲得“兩邊及其夾角對應相等的兩個三角形全等”的事實。通過例題的講解、變式訓練讓學生進一步認識到合情推理與演繹推理在幾何學習中是不可缺少的數學思想方法。

所以在幾何學習過程中，學生的推理能力得到了發展。

3.教學目的應面向全體，應用數學推理能力。

數學推理能力蘊含在數學知識的形成、發展和應用的過程中，數學推理能力不能僅靠教師對知識的講解、題目的分析與解決而幫助學生形成，更需要滲透在新知識的形成過程中。實際教學中，教師要多給學生提供參與教學活動的機會，通過觀察、實驗、操作、合作、探究，讓學生在充分參與教學活動的過程中真正感悟數學推理能力。

基于上述分析，數學推理能力的具體內涵為：通過對數學對象（數學概念、關系、性質、規則、命題等）進行邏輯性思考（觀察、實驗、歸納、類比、演繹），做出推論，再進一步尋求證據、給出證明或舉出反例說明所給出推論的合理性的一種綜合能力。數學推理不僅在幾何中根據公理、定義、定理、推論等證明有關結論，而且在代數中也是不可缺少的數學思想方式，例如有理數的計算、方程、不等式、函數、統計與概率等必須根據定義、法則、順序等進行推理進而達到解決問題的目的。在日常生活中也少不了數學推理能力，生活中遇到問題時，必須分析問題、找到解決問題的方法，在這個過程中，數學推理能力顯得更為重要。

（作者為江蘇省南京市第五初級中學教師）