課堂實錄:一個疑問引發的風波
楊平
(廣東省肇慶市端州區肇慶中學高中部)
課堂實錄:一個疑問引發的風波
楊平
(廣東省肇慶市端州區肇慶中學高中部)
在教學直線與雙曲線的位置關系時,為了讓學生更直觀地了解直線與雙曲線的交點情況,借用GeoGebra軟件進行演示。在演示中通過一個學生的疑問引導學生通過觀察、大膽質疑、自主探究、實踐求證,讓學生在數形結合的基礎上深入探討了直線與雙曲線的相關知識。
直線;雙曲線;數形結合;GeoGebra
GeoGebra是一個結合幾何、代數與微積分的動態數學軟件,它是由美國佛羅里達州亞特蘭大學的數學教授Markus Hohenwarter設計的,GeoGebra融合了代數與幾何兩大學科,做到了圖形與代數方程的同步變化,實現了真正的動態演示。可以通過在下方的命令輸入框輸入圓錐曲線方程的方式(如輸入“x^2+ y^2=1”)直接畫出圖形,甚至可以用向量運算的方式輸入(A+B+ C)/3來直接顯示△ABC的重心點。
一、波瀾不驚:常規教學在信息展示中傳授知識
在介紹直線與雙曲線的位置關系時,教師可以通過一個思考題來探究:討論直線y=kx-1與雙曲線x2-y2=1的交點個數,并求此時k的取值范圍。
代數解析不再贅述。為了讓學生更形象地理解直線與雙曲線的位置關系,利用GeoGebra軟件進行了下面設計:
①先在“輸入框”中分別輸入并回車:x^2-y^2=1,y=x,y=-x,得到雙曲線及其漸近線的圖象,可以很清晰地讓學生理解相切與只有一個交點的區別與聯系;
②在輸入框中輸入:y=kx-1,并回車,此時會彈出“創建滑動條”的對話框,根據需要產生一個關于變量k的滑動條(如下圖所示)。拉動滑動條,可讓學生與上面的代數式進行驗證。

二、風波乍起:點滴疑問在拓展思維中放飛思想
1.一個學生的積極歸納:
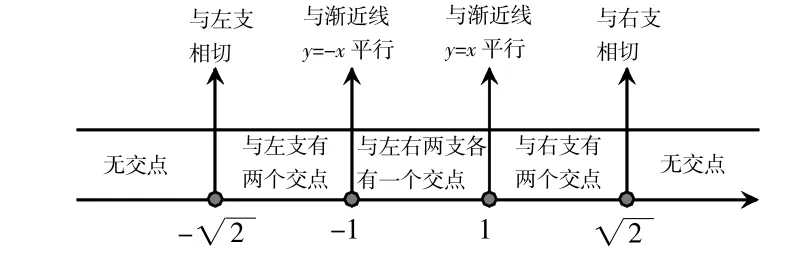
2.一個學生的無意提問:是否所有直線與雙曲線的位置關系都可以利用上面的數軸來實現呢?
3.要回答學生提出的問題,結合學生的嘗試和探討,教師可利用GeoGebra進行如下設計:
(1)先實現雙曲線x2-y2=1及其漸近線的圖象;
(2)在輸入框中輸入:y=tan(a)*(x-p)+q,其中a∈[0,3.14],p∈[-5,5],q∈[-5,5],從而形成過點M(p,q)的動直線d;
(3)在輸入框中分別輸入:y=(x-p)+q與y=-(x-p)+q,回車后形成過點M(p,q)的兩條與雙曲線漸近線平行的伴隨動直線;
(4)可以拖動點M,讓它位于不同的位置,再拖動參數a,觀察動直線d與雙曲線的交點情況。如下圖1所示:

圖1

圖2
(I)先研究直線與雙曲線只有一個交點的情形:將雙曲線包含兩個焦點的區域簡稱為雙曲線內,含有原點的區域簡稱為雙曲線外,如上圖2所示。通過定位點M(p,q)在圖2中的不同區域,可以觀察到下列情形:
①當點M在雙曲線內時,有兩條與雙曲線漸近線平行的直線與雙曲線只有一個交點;
②當點M在雙曲線上或點M在雙曲線的漸近線上(除原點)時,有三條直線與雙曲線只有一個交點:兩條與雙曲線漸近線平行的直線和一條與雙曲線相切的直線;
③當點M在雙曲線外左(右、上、下)區域時,有四條直線與雙曲線只有一個交點:兩條與雙曲線漸近線平行的直線和兩條與雙曲線相切的直線;
④當點M在原點處時,有兩條與雙曲線漸近線重合的直線與雙曲線只有一個交點。
(II)利用檢驗直線快速判斷直線與雙曲線的交點個數及此時所對應的直線斜率的變化范圍。下面是點M在雙曲線外左區域的檢驗圖形及結論。
這樣,我們就可以很快得到上面右方的結論,這也形成了解決直線與雙曲線交點問題的幾何法。

三、余波陣陣:大膽猜想在細致觀察中迸發靈感
1.通過觀察圖形的變化,學生大膽猜測:切線的斜率應該大于或小于。
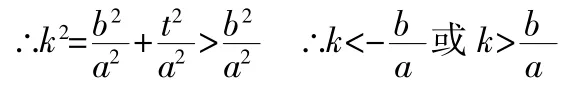
2.從圖象上思考:當點M位于漸近線上時,直線與雙曲線只有一條切線;當點M在雙曲線上時,直線與雙曲線只有一條切線,這兩種情形是否都意味著Δ=0時斜率k有兩個相等的實數根?
∴(p2-a2)x2-2pqk+q2+b2=0(※)
(1)當點M在x=±a上時,此時一條切線是x=±a,另一條切線的斜率為
(3)當點M位于雙曲線上時,則有b2p2-a2q2=a2b2,而(※)的Δ=(-2pq)2-4(p2-a2)(q2+b2)=0,有兩個相等的實數根。
四、波光粼粼:興趣探究在自我實踐中彰顯智慧
1.學生很好奇地利用GeoGebra軟件進行拋物線的自主學習。
2.學生很成功地利用GeoGebra軟件進行了雙曲線與橢圓等軌跡方程的再探究。
郭沫若老先生說過:“教育的目的是養成自己學習、自由研究、用自己的頭腦來想、用自己的手來做的這種精神。”課堂是老師的生命力所在地,是學生智慧的發源地。為了讓學生動起來,讓課堂活起來,讓愛充滿整個課堂,讓學生在樸素的課堂生活中去品味自然科學,我們要用師生之間的愛喚起學生的求知欲,用技巧引導學生全面和諧的發展,給學生創造一個民主和諧的發展空間。“數形結合拓思維,代數解析定經緯”,這堂課借用學生的疑問,引導學生自主觀察、大膽猜想、實踐求證、合作交流,讓學生真正成為課堂的主人。最有意義的是學生學會了使用數學工具軟件,并使之成為數學學習的重要助力。
詹文藝.過定點的直線與雙曲線的公共點問題淺析[J].學法指導,2013(41):95-96.
·編輯楊國蓉
楊平,男(1979—),碩士研究生,廣東省肇慶市端州區肇慶中學高中部數學教師。

