數(shù)學歸納法中運用歸納假設的策略

☉江蘇省運河高等師范學校 許榮良

數(shù)學歸納法中運用歸納假設的策略

☉江蘇省運河高等師范學校 許榮良

數(shù)學歸納法是高中數(shù)學解題過程中經常運用到的一種科學的證明方法，對于數(shù)學思維的培養(yǎng)也非常重要，解決問題具有實效快速等優(yōu)點.一般地，數(shù)學歸納法有兩個步驟：（1）證明當n取第一個值n0時命題成立.n0對于一般數(shù)列取值為0或1，但也有特殊情況.（2）假設當n= k（k≥n0，k為自然數(shù)）時命題成立，證明當n=k+1時命題也成立.綜合（1）（2），對一切自然數(shù)n（n≥n0），命題P（n）都成立.數(shù)學歸納法的第一步是驗證命題遞推的基礎，第二步是論證命題遞推的依據(jù)，兩個步驟密切相關，缺一不可.在運用數(shù)學歸納法證明命題時，對第二步n=k+1時結論的正確性的證明是整個證明過程中的重難點.我們除注意利用歸納假設外，還要注意對照結論充分利用其他數(shù)學證明方法，如放縮法、構造法等.也就是說，當我們利用歸納假設后仍不能直接變形推出結論時，需要采用下述方法進行證明，以達到目的.

一、與放縮法聯(lián)合

例1設實數(shù)c＞0，整數(shù)p＞1，n∈N*.求證：當x＞-1且x≠0時，（1+x）p＞1+px.

證明：用數(shù)學歸納法證明.

①當p=2時，（1+x）2=1+2x+x2＞1+2x，原不等式成立.

②假設p=k（k≥2，k∈N*）時，（1+x）k＞1+kx成立.

當p=k+1時，（1+x）k+1=（1+x）（1+x）k＞（1+x）（1+kx）=1+（k+1）x+kx2＞1+（k+1）x.

所以p=k+1時，原不等式也成立.

綜合①②可得，當x＞-1且x≠0時，對一切整數(shù)p＞1，不等式（1+x）p＞1+px均成立.

評注：放縮法是數(shù)學歸納法中常用的方法.本題從“k”過渡到“k+1”時，首先只能利用假設得到（1+x）k+1=（1+x）（1+x）k＞（1+x）（1+kx），將（1+x）（1+kx）展開得1+（k+1）x+kx2，與目標式子1+（k+1）x進行比較發(fā)現(xiàn)，需要減少一項kx2，故需要放縮.

二、與方程思想相伴

例2設數(shù)列｛an｝的前n和為Sn，滿足Sn=2nan+1-3n2-4n，n∈N*，且S3=15.

（1）求a1，a2，a3的值；

（2）求數(shù)列｛an｝的通項公式.

解析：（1）a1=S1=2a2-3×12-4×1=2a2-7，a1+a2=S2=4a3-3×22-4×2=4（S3-a1-a2）-20=4（15-a1-a2）-20，所以a1+a2=8.

綜上得a1=3，a2=5，a3=7.

（2）由（1）猜想an=2n+1，以下用數(shù)學歸納法證明：①由（1）知，當n=1時，a1=3=2×1+1，結論成立.

②假設n=k時，結論成立，即ak=2k+1.

則Sk=3+5+7+…+（2k+1）=

當n=k+1時，將ak+1和Sk代入Sk=2kak+1-3k2-4k中，得k（k+2）=2kak+1-3k2-4k，解得2ak+1=4k+6，故ak=2（k+1）+1，即n=k+1時，結論成立.

綜合①②可知對一切n∈N*，an=2n+1.

評注：此題證明中，首先利用假設得到Sk=k（k+2），再借助題設的關系式得到方程式Sk=2kak+1-3k2-4k，解出ak+1，證明n=k+1時命題成立，從而順利解題.

三、與構造法聯(lián)袂

例3求證：當n∈N*時，an+1+（a+1）2n-1能被a2+a+1整除.證明：（1）當n=1時，a2+（a+1）=a2+a+1能被a2+a+1整除.

（2）假設當n=k（k≥1且k∈N*）時，ak+1+（a+1）2k-1能被a2+a+1整除.

則當n=k+1時，ak+2+（a+1）2k+1=a·ak+1+a·（a+1）2k-1+（a+ 1）2k+1-a（a+1）2k-1=a·ak+1+a·（a+1）2k-1+［（a+1）2-a］（a+1）2k-1= a［ak+1+（a+1）2k-1］+（a2+a+1）（a+1）2k-1.

由假設可知a［ak+1+（a+1）2k-1］能被a2+a+1整除，而且（a2+a+1）（a+1）2k-1也能被a2+a+1整除，所以ak+2+（a+1）2k+1也能被a2+a+1整除，即n=k+1時命題也成立.

綜合（1）（2）知，對任意的n∈N*命題都成立.

評注：（1）在證明n=k+1時，不僅要將ak+2分離為a·ak+1，而且要構造出相關項a·（a+1）2k-1，加一項減一項即得a· ak+1+a·（a+1）2k-1+（a+1）2k+1-a（a+1）2k-1，整理出a［ak+1+（a+ 1）2k-1］后還有（a2+a+1）（a+1）2k-1，兩者均能被a2+a+1整除，故命題得證.（2）利用數(shù)學歸納法證明等式或整除問題，關鍵是利用加、減項，拆、并項等恒等變形的方法，構造出假設、結論的結構形式.

四、與函數(shù)單調性相遇

（1）討論f（x）的單調性；

（2）設a1=1，an+1=ln（an+1），證明：

例4函數(shù)解析：（1）f（x）的定義域為（-1，+∞），f′（x）=

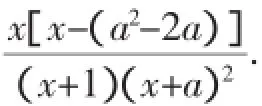
①當1＜a＜2時，若x∈（-1，a2-2a），則f′（x）＞0，f（x）在（-1，a2-2a）上是增函數(shù)；若x∈（a2-2a，0），則f′（x）＜0，f（x）在（a2-2a，0）上是減函數(shù)；若x∈（0，+∞），則f′（x）＞0，f（x）在（0，+∞）上是增函數(shù).

②當a=2時，f′（x）＞0，當且僅當x=0時f′（x）＞0成立，f（x）在（-1，+∞）上是增函數(shù).

③當a＞2時，若x∈（-1，0），則f′（x）＞0，f（x）在（-1，0）上是增函數(shù)；若x∈（0，a2-2a），則f′（x）＜0，f（x）在（0，a2-2a）上是減函數(shù)；若x∈（a2-2a，+∞），則f′（x）＞0，f（x）在（a2-2a，+∞）上是增函數(shù).

（2）由（1）知，當a=2時，f（x）在（-1，+∞）是增函數(shù).當 x∈（0，+∞）時，f（x）＞f（0）=0，即ln（x+1）＞.又由（1）知，當a=3時，f（x）在［0，3）上是減函數(shù)；當x∈［0，3）時，f（x）＜f（0）=0，即ln（x+1）

根據(jù)①②知對任何n∈N*結論都成立.

評注：第（2）步中應用假設可以得到ak+1=ln（ak+1）＞但是無法得到本題在第（1）步中，討論f（x）的單調性已經為證明第（2）步做好了準備，所以需要應用a=2和a=3時函數(shù)f（x）的單調性才能進一步推導得到.

五、有加強命題相助

例5設a1=1，an+1=

（1）若b=1，求a2，a3及數(shù)列｛an｝的通項公式；

（2）若b=-1，問：是否存在實數(shù)c使得a2n＜c＜a2n+1對所有n∈N*成立？證明你的結論.

因為a1=，因此猜想an

下用數(shù)學歸納法證明上式：

①當n=1時結論顯然成立.

②假設n=k時結論成立，即ak

下用數(shù)學歸納法證明加強命題a2n＜c＜a2n+1＜1.

②假設n=k時結論成立，即a2k＜c＜a2k+1＜1.

易知f（x）在（-∞，1］上為減函數(shù)，從而c=f（c）＞f（a2k+1）＞f（1）=a2，即1＞c＞a2k+2＞a2.

再由f（x）在（-∞，1］上為減函數(shù)，得c=f（c）＜f（a2k+2）＜f（a2）=a3＜1.

故c＜a2k+3＜1，因此a2（k+1）＜c＜a2（k+1）+1＜1.這就是說，當n= k+1時結論成立.

評注：有些關于正整數(shù)n的命題P（n），直接用數(shù)學歸納法處理難以實現(xiàn)n到n+1的過渡，但是證明比P（n）更強的命題Q（n），用數(shù)學歸納法進行證明反而簡單一些，此時需要對命題進行加強.選擇加強命題要合適恰當，這樣才能順利過渡.數(shù)學歸納法是高中數(shù)學解題過程中經常運用到的一種科學的證明方法，解決與自然數(shù)有關的命題P（n）實效快速.對于數(shù)學思維的培養(yǎng)也非常重要.F