舵機卡死對X型舵飛航導彈控制性能的影響

林 木,賈旭山,張 凱

(中國人民解放軍92941部隊,遼寧 葫蘆島 125000)

?

舵機卡死對X型舵飛航導彈控制性能的影響

林 木,賈旭山,張 凱

(中國人民解放軍92941部隊,遼寧 葫蘆島 125000)

建立了X型舵飛航導彈舵機卡死故障條件下執行機構輸入與輸出的關系模型,分析了舵機卡死引起舵效降低、常值誤差和控制耦合三方面效應對導彈控制性能的影響。為考察不同時刻舵機卡死影響的差異,建立了導彈六自由度數學模型。仿真結果表明,單個舵機卡死會造成導彈控制性能下降,命中點散布變大;在一些極端初始條件下,俯仰和偏航通道產生嚴重的控制耦合,會使彈道畸變,導致導彈墜落。對飛行試驗中出現的案例進行分析,驗證了仿真分析結論的正確性。

飛航導彈;飛行控制系統;舵機故障;彈道仿真

飛航導彈的操縱面包括升降舵面、方向舵面和副翼,其中升降舵提供俯仰力矩,方向舵主要提供偏航力矩,副翼主要提供滾轉力矩[1]。導彈常用的舵面布置方案中,“十”字型布置的升降舵和方向舵相互獨立,一旦其中某個操縱面出現故障,如執行機構鎖死或者歸零等,將造成嚴重的后果[2-3]。而采用“×”型舵的導彈可由多個舵面同時提供控制力矩,提高了導彈控制的容錯能力,即使某一個舵機出現了故障,故障舵面提供的控制力矩可由其他舵面代替產生,導彈仍然具有一定的控制能力。

本文以反艦導彈為研究對象,分析“×”型布局下單個舵機卡死故障對導彈控制性能的影響,并以導彈飛行試驗中出現的舵機卡死故障為案例進行了驗證。

1 舵機執行機構輸入輸出模型

1.1 舵控指令的分配

某型反艦導彈采用尾舵控制的“×-×”型氣動外形布局,中部固定式彈翼與尾舵安裝角度相同,彈翼負責為導彈提供升力,尾舵由4個舵機共同完成導彈俯仰、偏航和滾轉的控制。圖1是該型導彈尾舵配置方案的后視圖。舵機編號沿導彈縱軸逆時針依次為D1、D2、D3和D4;y和z分別為彈體系y軸、z軸的指向;圖中舵面附加方塊表示舵面正向偏轉時舵面后緣在后視圖的投影。三通道舵控信號與4個舵面偏轉角的等效關系寫成矩陣形成為式中:δx,δy,δz分別為滾轉、偏航和俯仰三通道舵控信號;d1,d2,d3,d4為4個舵面的偏轉角。

(1)

式(1)使用3個方程約束了4個未知數,該方程組有無窮多解,為充分利用4個舵面的控制能力,使舵面控制有最小二乘意義下的最優解,使用Penrose-Moore偽逆法求解[4],得到該型導彈舵控指令號分配如下:

(2)

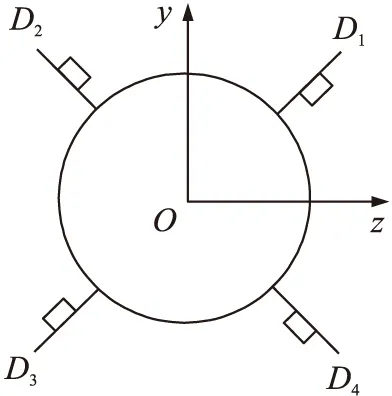
圖1 X型操縱舵面正向偏轉后視圖

1.2 舵機卡死后執行機構模型

設在某時刻之后,導彈4號舵機卡死,舵機卡死時刻三通道控制指令信號為δx0、δy0和δz0,則4號舵機卡死后,式(2)中的導彈舵控指令分配模型變為

(3)

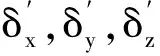
(4)

觀察式(4)中的第3項,舵機卡死后,在通道間產生了控制耦合,比如滾轉通道中,引入了偏航和俯仰控制的差指令信號0.25(δy-δz)。這樣將導致各通道間的控制相互影響,造成導彈穩定性變差,根據式(4),某一通道控制耦合程度的大小取決于另外2個通道的和信號或差信號。

2 舵機卡死故障影響理論分析

2.1 舵效降低的影響

如果把式(4)中的常值誤差項和耦合項看作是滿足特定規律的外來擾動,那么在舵機卡死后,相當于舵系統的開環放大系數降低了25%,傳遞函數的形式不變,下面分析開環放大系數降低帶來的影響。

通常,舵系統中需要引入反饋,以提高執行機構的快速性和穩定性,改善執行機構的性能。圖2是采用位置反饋的舵系統框圖,通過測量舵機偏轉位移量X,并反饋回舵控信號,可以提高舵機的響應速度和穩定性,進而提高整個舵系統的性能。考慮是在負載情況下,氣動舵機的動力學特性可用慣性環節表示,圖2所示的舵系統可以用圖3描述[5]。圖中,KZF和KDJ為綜放和舵機放大系數,KOC為反饋系數,iK為舵控信號,τDJ為舵機時間常數,tDJ為舵機延遲時間。

圖2 帶位置反饋的舵系統結構圖

圖3 帶負載的舵系統框圖

對圖3中采用硬反饋(反饋滿足線性條件)的舵系統來說,開環放大系數K0=KZFKDJKOC是影響其動態品質的最重要因素,K0越大,舵系統的快速響應越好。當K0足夠大并且忽略舵機本身的慣性時,即tDJ≈0,則舵系統的時間常數τDX滿足[5]:

(5)

由此可見,舵系統開環放大系數降低會導致時間常數增大,影響其響應速度。根據文獻[6]的分析,舵系統時間常數的增大會對制導系統的命中精度產生不良影響。此外,舵系統開環放大系數的減小還會導致整個回路相對阻尼系數減小[5],進而導致導彈姿態角控制的超調量增大,影響導彈姿態穩定控制品質。

2.2 常值誤差的影響

根據式(4),舵機卡死帶來的常值誤差等于舵機卡死時刻舵控指令信號的代數和,該值大小不會隨時間的推移發生變化,因此可以看作是在導彈控制回路中施加了一個階躍擾動力矩。

通常情況下,反艦導彈姿態控制系統通過引入積分環節來消除系統靜差,因為控制系統中包含積分控制作用,只要終值誤差不為0,控制系統就一定會產生一個持續增長的輸出力矩來抵消階躍力矩的作用,力圖減小這個誤差,只有當終值誤差等于0時,才使得控制系統輸出的力矩與階躍擾動力矩大小相等而方向相反,這時系統取得平衡進入穩態[7]。

在系統進入穩態以前,導彈的位置變量會產生偏移,即導彈實際彈道相比于理論彈道會產生偏差,尤其對于不引入位置反饋的偏航通道來說,姿態調整會產生較大的位置偏差。因此,如果舵機卡死時刻接近飛行末端,舵機卡死會導致制導命中精度下降,其他情況下,導彈控制系統基本可以消除常值誤差帶來的影響。

2.3 控制耦合的影響

對系統內部耦合程度進行定量分析時,可使用相對增益[8]來衡量輸入量uj對輸出量yi的影響。這里把舵控指令作為輸入量,把實際舵面偏轉角度作為輸出量,相對增益矩陣可寫為

(6)

式中:λ11,λ22,λ33分別為滾轉、偏航和俯仰通道的相對增益,可以表征其耦合程度,其計算公式可以表示為

(7)

式中：pij為輸入通道uj到輸出通道yi的開環增益系數,qij為輸入通道uj到輸出通道yi的閉環增益系數。相對增益為1時,通道無耦合作用,工程上認為,相對增益大于1.2或者在0.37～0.7之間時,通道之間耦合情況比較嚴重。經計算,舵機卡死后,三通道相對增益均為1.5,控制耦合比較嚴重。

3 導彈六自由度仿真及分析

為了分析舵機卡死時刻不同對導彈制導命中精度的影響,建立了導彈六自由度模型,進行仿真計算。仿真過程中,由制導律解算模塊給出三通道控制指令,然后根據式(2)進行舵面轉換,得出實際的舵機偏轉角度,再將實際偏轉角度輸入彈體動力學及運動學模塊進行解算。整個導彈仿真模型數據流如圖4所示。圖中,Fp和Fx,Fy,Fz為導彈受到的推力和空氣動力;Fcx,Fcy,Fcz為舵機產生的控制力;Msty、Mstz,Mdx、Mdy、Mdz,Mcx、Mcy、Mcz依次為導彈受到的穩定力矩、阻尼力矩和操縱力矩;α、β、γV,αW、βW、γVW分別為導彈不考慮風以及考慮風的攻角、側滑角和速度傾斜角;θ,ψV分別為彈道傾角和彈道偏角;?,φ,γ分別為俯仰角、偏航角和滾轉角;ωx,ωy,ωz為姿態角速度;vW,v,Ma,q分別為風速以及導彈的速度、馬赫數和動壓;m為導彈質量;Jx,Jy,Jz為轉動慣量;x、y、z,xt、yt、zt分別為導彈和目標的位置;h,hm分別為導彈高度與測量高度。

不考慮目標運動和隨機風的影響,以舵機正常情況下導彈制導命中脫靶量(導彈實際命中點相對于理論命中點的偏差,用高度脫靶量和側向脫靶量表示)的均值和標準差作為參照,在導彈飛行初段、轉彎降高段和飛行末段3個特征點,分別仿真研究舵機卡死故障對導彈控制性能的影響。參考彈道飛行總時間55 s,35 s完成轉彎降高,發射扇面角2.01°,目標高度5 m。舵機正常工作時,側向脫靶量均值-1.5 m,標準差0.7 m,高度脫靶量均值-0.6 m,標準差0.1 m。導彈飛行10 s,30 s和50 s時設定4號舵機卡死,仿真500次,側向脫靶量均值分別為-2.6 m,-2.7 m和-2.6 m,標準差分別為0.4 m,0.4 m和0.5 m;高度脫靶量均值分別為-0.2 m,-0.7 m和-1.6 m,標準差分別為0.5 m,0.5 m和0.2 m。命中點散布如圖5所示。圖中,Δh和ΔX分別為高度脫靶量和側向脫靶量。

圖4 導彈六自由度仿真模型數據流向圖

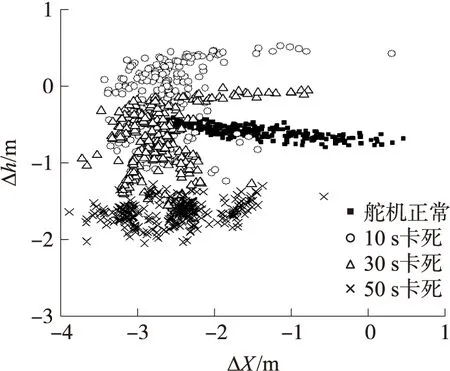
圖5 導彈仿真命中點散布圖

通過上述分析,舵機卡死后,導彈控制性能下降,命中點散布變大,有可能導致導彈脫靶。另外仿真過程中還發現,某些極端初始條件下,控制耦合作用嚴重時,偏航通道的轉彎控制信號會造成導彈降高時高度發生振蕩,使導彈墜落,如圖6所示。

圖6 控制耦合造成導彈飛行高度振蕩示意圖

4 舵機卡死故障案例分析

飛行試驗中,在某時刻之后,導彈4號舵機卡死,直至導彈飛行結束。試驗數據表明(圖7),4號舵機卡死后,彈體開始小幅振蕩并逐步收斂,俯仰通道受到的影響最小,傾斜和偏航通道受影響較大,出現了同頻振蕩,振蕩調整后彈體趨于穩定,最終仍命中目標,脫靶量與正常飛行情況相比偏大。

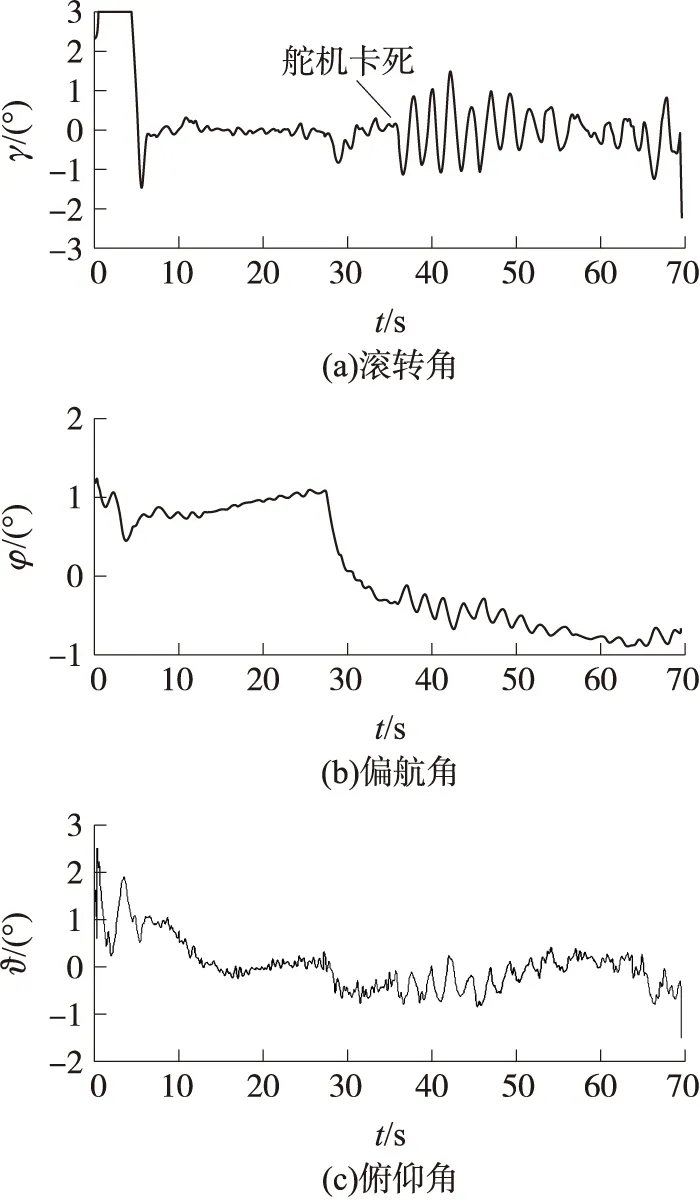
圖7 故障導彈姿態角

由前面2.3節分析可知,三通道的相對增益是相同的,但在系統實際運行中,各通道耦合信號的大小是有區別的。這里將式(4)中的第3項定義為耦合舵偏角,分別記作Δδx,Δδy和Δδz,根據試驗數據,各通道耦合舵偏角見圖8。可以看出,偏航和滾轉通道的耦合舵偏角比俯仰通道大,這是導致滾轉、偏航通道的振蕩幅度大于俯仰通道的主要原因。另外,各通道傳遞函數的階次和參數不同,也是導致這一現象的原因之一,這里不再贅述[9]。可見,前面的理論分析解釋了該案例的故障現象,為該次試驗故障定位提供了理論依據。

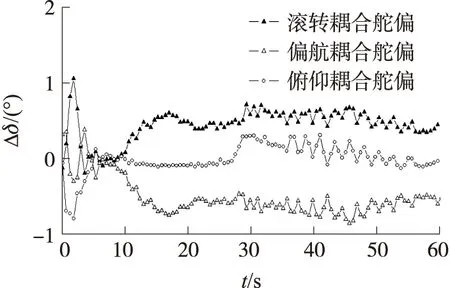
圖8 三通道耦合舵偏角

5 結束語

本文研究了舵機故障對“×”型舵飛航導彈控制穩定性能的影響,分析了舵機故障對導彈控制產生影響的機理,包括舵效降低、常值誤差和控制耦合,并進行了仿真分析計算。仿真計算結果表明,單個舵機卡死后,一般情況下導彈可以依靠冗余的舵機完成控制飛行,但控制性能下降,命中點散布變大,側向脫靶量均值由-1.5m增大到-2.6～2.7m,高度脫靶量由-0.6m增大到-0.7～-1.6m。在一些特定的初始條件下,舵機卡死還會導致導彈墜落。本文對“×”型舵機卡死故障影響的理論分析,可為類似故障現象定位提供參考依據。

[1] SIOURIS G M.導彈制導與控制系統[M].張天光,王麗霞,宋振峰,譯.北京:國防工業出版社,2010:105-106.

[2]杜鳳懷,王蕭,孫虎員.舵機卡死故障的導彈容錯控制研究[J].彈箭與制導學報,2008,28(5):68-72. DU Feng-huai,WANG Xiao,SUN Hu-yuan.Fault-tolerant control on missile rudder deadlock[J].Journal of Projectiles,Rockets,Missiles and Guidance,2008,28(5):68-72.(in Chinese)

[3]李江濤.典型故障模式下飛航導彈容錯與重構算法研究[D].哈爾濱:哈爾濱工業大學,2010. LI Jiang-tao.Research of fault tolerant and reconfiguration algorithm on winged missile with typical failuers[D].Harbin:Harbin Institute of Technology,2010.(in Chinese)

[4]靳凌,董繼鵬.考慮舵機故障的空空導彈飛行控制系統主動容錯控制[J].彈箭與制導學報,2014,34(6):5-7. JIN Ling,DONG Ji-peng.Active fault-tolerant flight control system design of air-to-air missile considering rudder faults[J].Journal of Projectiles,Rockets,Missiles and Guidance,2014,34(6):5-7.(in Chinese)

[5]彭冠一.防空導彈武器制導控制系統設計[M].北京:宇航出版社,2005. PENG Guan-yi.Air defense missile guidance control system design[M].Beijing:China Astronautic Publishing House,2005.(in Chinese)

[6]王旭剛,王中原.彈體滾速和舵機時間常數對炮彈制導精度的影響[J].南京理工大學學報,2011,35(2):182-186. WANG Xu-gang,WANG Zhong-yuan.Effect of roll angular velocity and actuator time constant on guidance precision of guided projectile[J].Journal of Nanjing University of Science and Technology,2011,35(2):182-186.(in Chinese)

[7]胡壽松.自動控制原理[M].北京:國防工業出版社,1990. HU Shou-song.Automatic control theory[M].Beijing:National Defense Industry Press,1990.(in Chinese)

[8]孫瑞勝,薛曉中,付琳.一種制導炸彈的側向運動的解耦控制[J].彈箭與制導學報,2005,24(3):110-112. SUN Rui-sheng,XUE Xiao-zhong,FU Lin.Decoupling control for a guided bomb’s horizontal movement[J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,24(3):110-112.(in Chinese)

[9]孟秀云.導彈制導與控制系統原理[M].北京:北京理工大學出版社,2003:31-34. MENG Xiu-yun.Missile guidance and control system theory[M].Beijing:Beijing Institute of Technology Press,2003:31-34.(in Chinese)

Effect of X-Rudder Locking on Control Performance of Cruise Missile

LIN Mu,JIA Xu-shan,ZHANG Kai

(Unit 92941 of PLA,Huludao 125000,China)

A relationship model of input and output of X-rudder missile servo system under locking fault conditions was established.The influences of three aspects caused by a stagnation fault of servo system on control performance of missile were researched,including the descent of rudder effect,the introduction of constant error and the coupling of control system.In order to investigate the difference when missile servo system was locked at different time,a six-degree-of-freedom model of missile was established.The simulation result shows that one rudder locking can result in control performance degradation and impact point dispersion increase of missile.Under some extreme initial conditions,the pitch channel and yaw channel coupling can cause missile dropping.A case in flight test was analyzed,which verified the correctness of the simulation analysis conclusion.

cruise missile;flight control system;rudder fault;trajectory simulation

2016-06-12

林木(1983- ),男,工程師,學士,研究方向為裝備試驗。E-mail:rs023@163.com。

TJ761.5

A

1004-499X(2016)04-0052-05