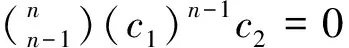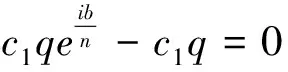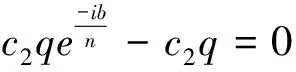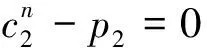涉及差分算子的兩個問題
丁 杰
(太原理工大學 數學學院,太原 030024)
?
涉及差分算子的兩個問題
丁 杰
(太原理工大學 數學學院,太原 030024)
考慮整函數與其差分算子分擔集合的唯一性問題。假設,f為非常數整函數,且滿足λ(f)<ρ(f)<∞;a(z),b(z)是兩個不同的非常數整函數,使得ρ(a)<ρ(f)和成立。若f與ΔcfCM分擔a(z),b(z),則Δcf(z)≡f(z).
整函數;差分;特征函數
假設,f是定義在復平面C上的亞純函數。運用Nevanlinna理論中的經典記號,如:T(r,f)表示函數f的特征函數;m(r,f)表示近似函數;N(r,f)表示數目函數[1-2]。 另,記S(r,f)表示特征函數的無窮小量,即: 當r→∞且除去r的一個有限線測度外S(r,f)=oT(r,f)成立;當亞純函數α(z)滿足T(r,α(z))=S(r,f)時,稱α(z)為f的小函數。 為了定理的敘述方便,筆者給出以下定義。
定義1 如果Q(z,f)為關于f,f′以及f的差分f(z+c)的多項式,且多形式的系數為f的小函數。 則稱Q(z,f)為一個差分微分多項式。
Nevanlinna值分布理論在唯一性、復微分方程、正規族等領域有很多應用,這些應用不僅簡化了許多原定理的證明,更豐富了原來的理論,得到更多的定理。
1982年GROSSetal[3]證實了下述定理。
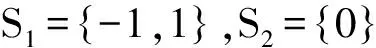
隨后,有許多數學工作者關注涉及分擔集合的唯一性問題[4-8]。
Nevanlinna理論中對數導數引理是證明第二基本定理的基礎。 正如對數導數引理在Nevanlinna理論中的作用一樣,有窮級條件下對數導數引理對應的差分形式的證明奠定了差分Nevanlinna理論的研究,這個證明的證明是由HALBURDetal[9]與CHIANGetal[10]分別獨立完成。 近幾年涉及差分形式的值分布理論成為研究的熱點問題之一,同時許多數學工作者開始研究涉及差分的唯一性問題和復差分方程[11-14]。
在文獻[15]中,LIetal證實了下述定理。
定理B假設f為非常數整函數且滿足λ(f)<ρ(f)<∞,ρ(f)≠1;a(z),b(z)是兩個不同的非常數整函數使得ρ(a)<ρ(f)和成立。 若f與ΔcfCM分擔a(z),b(z),則Δcf(z)≡f(z).
在本文中,減弱了定理B的假設條件,從而改進了上述結果,得到了如下定理。
定理1 假設f為非常數整函數且滿足λ(f)<ρ(f)<∞;a(z),b(z)是兩個不同的非常數整函數使得ρ(a)<ρ(f)和成立。若f與ΔcfCM分擔a(z),b(z),則Δcf(z)≡f(z).
YANGetal[7]證明了一個關于差分方程的結果。
定理C假設q(z)為非常數多項式且b,c∈C為非零常數,則非線性差分方程f3(z)+q(z)f(z+1)=csinbz,
不存在有窮級的整函數解。
在文中,筆者解決了上述問題并得到了以下定理。
定理2 考慮非線性差分方程
(1)
式中:b≠0,p1,p2∈C為常數且p1·p2≠0,n≥3為正整數。
當q(z)為非常數多項式時,式(1) 不存在有窮級整函數解。
當q(z)=q為非零常數且n≥4,式(1) 不存在有窮級整函數解。
1 引理
為了證明定理,需要下面的引理。
引理1 假設fj(j=1,…,n) (n≥2)為亞純函數,gj(z) (j=1,…,n)為整函數且滿足:
2) 當1≤j 3) 當1≤j≤n,1≤h 其中,E?(1,∞)為有限的線測度或對數測度。則對所有的j=1,…,n有fj≡0. 引理2 設f為有窮級的超越亞純函數,考慮差分方程H(z, f)P(z, f)=Q(z, f),其中H(z, f),P(z, f)和Q(z, f)為關于f的差分多項式且H(z, f)關于f和f的差分的總次數為n,Q(z, f)的總次數不大于n. 若H(z, f)中最大次數僅有一項,則對任意的ε>0,至多除去一個有窮的對數測度外有:m(r,P(z,f))=O(rρ-1+ε)+S(r,f). 引理3 假設c為一個非零常數且α為一個非常數的亞純函數,則微分方程f2+(cf(n))2=α無超越亞純解,滿足T(r,α)=S(r,f). 假設f是一個整函數且滿足λ(f)<ρ(f)<∞,則根據Hadamard因子分解定理f可以表示為: (2) 式中,Q(z)=aqzq+…+a1z+a0為多形式且滿足λ(f)=λ(P)=ρ(P) 根據Δcf的定義以及式 (2),可以得到: (3) 式中,ρ(H) (4) 式中,α(z)為多項式。 結合式(2),式(3) 和式 (4),有: (5) 如果α(z)不是一個常數,則應用定理的假設條件ρ(a)<ρ(f),ρ(b)<ρ(f) 以及 引理1,得到矛盾。 因此,α(z)為一個常數。 而引理 1 暗含α(z)≡0,所以式(4) 可以寫為: 因此f(z+c)=a(z)+b(z)或者Δcf(z)-f(z)=0成立,而根據假設條件ρ(a)<ρ(f),ρ(b)<ρ(f)可得:f(z+c)≠a(z)+b(z). 所以有Δcf(z)≡f(z). 這就完成了定理1的證明。 假設f為原方程的一個整函數解,則f一定是超越的。 對方程左右兩邊分別求微分運算,然后得到: 其中,Tn(z,f)為關于函數f的一個微分差分多項式,次數不超過n. (6) 否則,將引理2應用到上述微分差分方程有: (7) 因此,α:=b2f2+n2(f′)2是函數f的一個小函數且不恒等于零。 根據引理3,α一定為一個常數。 對b2f2+n2(f′)2=α左右兩邊分別進行微分運算可以得式(6)成立。 進一步對式(6)求解,可以看出f是下述形式: (8) (9) 對上式進行簡化有: (10) 下面根據n的奇偶性分兩種情況討論: 情況1 如果n是偶數,且w(z)為一個超越函數,則有: ? ? (11) 上式一共n+3個式子,分別標號(1),(2),…,(n+3). 由式(1)和式(n+3)可得c1≠0,c2≠0. 但是式(n+1)和式(n+2)暗含q(z)為一個常數且q(z)≠0,由式(2),(3),…,(n)中任何一個式子都可以推出c1=0,c2=0. 這明顯是個矛盾,因此式(11)不存在有窮級的整函數解。 情況2 如果n是奇數,且w(z)為一個超越函數,不得不再分兩種情況。 1) (12) 既然w(z)是超越的,則一定有: (13) 上式一共(n+3)個式子,分別標號(1),(2),…,(n+1).由式(1)和式(n+1)易得c1≠0,c2≠0. 但是式(3)和式(4)暗含q(z)為一個常數,q(z)≠0且(2),(3),…,(n)中任何一個式子都可以推出c1=0,c2=0. 這樣得到一個矛盾,因此原方程不存在有窮級整函數解。 2) 若n=3,則簡化式(9),可得到: (14) 既然w(z)是超越的,則有: (15) [1] 楊樂.值分布論及其新研究[M].北京:科學出版社,1982. [2] 儀洪勛,楊重駿.亞純函數唯一性理論[M].北京:科學出版社,1995. [3]GROSSF,OSGOODCF.Entirefunctionswithcommonprimates,in:FactorizationTheoryofMeromorphicFunctions[J].MarcelDekker,1982:19-24. [4]FRANKG,REINDERSM.Auniquerangesetformeromorphicfunctionswith11elements[J].ComplexVariableTheoryAppl,1998,37(1):185-193. [5]LIP,YANGCC.Somefurtherresultsontheuniquerangsetsofmeromorphicfunctions[J].KodaiMathematicalJournal,1995,18:437-450. [6]YIHX.UniquenessofmeromorphicfunctionsandaquestionofGross[J].ScienceinChina(Ser.A),1994,37(7):802-813. [7]YIHX,YANGLZ.Meromorphicfunctionsthatsharetwosets[J].KodaiMathematicalJournal,1997,20(2):127-134. [8]ZHANGQC.Meromorphicfunctionssharingthreevalues[J].IndianJournalofPure&AppliedMathematics,1999,30:667-682. [9]HALBURDRG,KORHONENRJ.Nevanlinnatheoryforthedifferenceoperator[J].Annales-AcademiaeScientiarumFennicaeMathematica,2005,31(2):463-478. [10] CHIANG Y M,FENG S J.On the Nevanlinna characteristic off(z+a) and difference equations in the complex plane[J].The Ramanujan Journal,2008,16(1):105-129. [11] LAINE I,YANG C C.Clunie theorems for difference and q-difference polynomials[J].Journal of the London Mathematical Society,2007,76(3):556-566. [12] LAINE I,YANG C C.Tropical versions of Clunie and Mohon′ ko lemmas[J].Complex Variables & Elliptic Equations,2010,55(1/2/3):237-248. [13] YANG C C,LAINE I.On analogies between nonlinear difference and differential equations[J].Proceedings of the Japan Academy(Ser. A),2010,86:10-14. [14] ZHANG J L.Value distribution and shared sets of differences of meromorphic functions[J].Journal of Mathematical Analysis & Applications,2010,367(2):401-408. [15] LI X M.Entire functions sharing a finite set with their difference operators[J].Computational Methods & Function Theory,2012,12(1):307-328. [16] LI P,YANG C C.On the nonexistence of entire solutions of certain type of linear differential equations[J].Journal of Mathematical Analysis & Applications,2006,320(2):827-835. [17] YANG C C,YE Z.Estimates of the proximate function of differential polynomials[J].Proceedings of the Japan Academy,2007,83(4):50-55. (編輯:朱 倩) Two Problems about Difference Operator DING Jie (Collage of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China) In this paper, we investigate the uniqueness theorem of entire functions sharing sets with its difference operators. Suppose thatfbe a non-constant entire function satisfyingλ(f)<ρ(f)<∞,a(z),b(z) be different non-constant entire functions such thatρ(a)<ρ(f).Letfand Δcfsharea(z),b(z) CM, thenΔcf(z)≡f(z). entire functions;difference;characteristic function 1007-9432(2016)04-0541-04 2014-09-16 山西省自然科學基金資助項目:Hayman 定理的差分對應定理的研究(2014021009-3);山西省歸國留學人員科研基金資助項目:一類復差多分項式值分布及正規族問題的研究(2013-045) 丁杰(1984-),男,太原人,博士,講師,主要從事基礎數學的研究,(E-mail)dingjie@tyut.edu.cn O174.52 A 10.16355/j.cnki.issn1007-9432tyut.2016.04.0212 定理1的證明
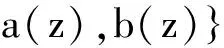
3 定理2的證明