借力學生問題引活課堂氛圍
江蘇省揚州市江都區邵伯高級中學(225200)
張莉莉●
?
借力學生問題引活課堂氛圍
江蘇省揚州市江都區邵伯高級中學(225200)
張莉莉●
本文通過學生對一道題求解中的疑惑,引導學生深入探究,發現問題所在,激活課堂氛圍,收獲頗豐.
課堂氛圍;學生主體;形成性評價
新課程改革以來,一直強調以學生為主體,以教師為主導的這樣一種角色定位,與此理念相一致的課程評價如火如荼,從以前比較單一的對學生學習效果的評價——即考試與測驗,甚至更粗放就是學生考試成績的量化,到現在教師教學工作(教學設計、組織、實施等)的評價——教師教學評估(課堂、課外)與對學生學習效果的評價——即考試與測驗相結合. 評價的方法主要有量化評價和質性評價.我們在欣賞量化評價的“理性”的同時,也不可忽略質性評價的“感性”.活躍課堂教學氣氛,激發學生的學習興趣,讓學生的思維在課堂上充分活躍起來,也能促使教學任務順利完成.課堂教學中的形成性評價要限時完成,肯定學生的成績,找出問題,及時糾正,消除學生的錯誤積累,順利實現課堂教學目標.這種 在教學過程中進行的評價稱為形成性評價.它以測驗或檢查的方式及時明確學生所要達到的程度,并發現存在的問題,從而隨時修正和調節教學和學習活動.形成性評價的目的是為了控制教學過程,從而使全體學生都能達到教學目的.活躍課堂教學氣氛,激發學生的學習興趣,讓學生的思維在課堂上充分活躍起來,也能促使教學任務順利完成.課堂教學中的形成性評價要限時完成,肯定學生的成績,找出問題,及時糾正,消除學生的錯誤積累,順利實現課堂教學目標.高三的幾輪復習中,有時候我們不妨借力學生的問題引活課堂氛圍,達到高考復習所要求的綜合能力提升.

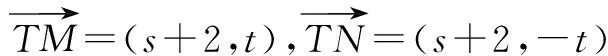
總結如下:利用解析幾何的大環境以坐標處理向量數量積,再通過代入消元,將二元函數最值轉為一元函數在已知區間上求最值.
講解完整個過程后,學生甲提出能否聯立圓與橢圓方程,通過r來表示M,N的坐標,繼而表示出一個有關于r的函數去處理.
我表示同意,并且補充他的思路和講解思路大方向一致,均是利用函數求最值,只不過自變量選擇不同而已.
學生甲困惑地說他遇到了大麻煩,以致于都懷疑自己整個解題的思路.
我請所有的同學參與到這次解惑過程中,并請學生積極發表自己的見解.
學生乙:好像沒什么問題啊!是不是理論行,實際操作就是不行,我們也遇到過不少的.不過我們遇到的似乎是計算上的繁瑣,倒不像這邊遇到的得出了矛盾,明顯是思路有問題.
這時全班陷入了更大范圍的疑惑.對照我的講解(做對的學生跟我講解的處理大多一致)和學生甲的過程不知問題出在哪.
突如其來的障礙還是學生“設置”的,很多人精神振奮起來.
我還是堅持一開始的判斷,并且回顧了學生甲的理論支持.在平面解析幾何初步(江蘇教育出版社普通高中課程標準實驗教科書必修2第2章)中我們研究了平面中直線與直線的位置關系,直線與圓的位置關系,甚至在選修2-1第2章圓錐曲線與方程第2.6.3曲線交點這節內容也用了聯立方程組求解來確定交點坐標.在直線與圓的位置關系中,我們還強調在此有幾何和代數兩種處理方法,雖然此關系中更多的是用幾何方法,但遇到直線與圓錐曲線位置關系中,圓錐曲線少了圓那么優良的幾何性質,就只剩下代數方法了.從這個意義上講,代數方法更具普遍適用性.
當然我并沒有直接說出原因,而是創設一個簡單熟悉的情境.求圓C:x2+y2=2與拋物線y2=x的交點坐標.
學生們通過聯立方程組,很快可以解出x1=-2,x2=1,通過圖形或是拋物線的簡單幾何性質知,交點橫坐標必須大于零,所以必須舍掉一個負根.并且不知道這個簡單的問題對剛剛的疑惑有何幫助.我請同學注意對比學生甲的過程和我們都認為簡單的這道題過程.
還是同學甲自己發現了問題,他說根與系數關系利用的時候,我們是用一元二次方程的兩實數根,類比到老師的例子中就是-2和1,而實際曲線交點只是1!我點頭表示贊許,并問大家如何規避這個問題呢?
學生丁提出利用圖象,可以看到消元之后方程根的初步范圍來處理.在同學甲的過程中,我們可以利用求根公式算出兩根,借助r的范圍,求出根的范圍再決定究 竟要哪個根.
通過上面解惑的過程我們可以發現方法本身并沒有問題,但消元后方程的解要根據實際問題變成某個區間上的解,其實就是我們在消元思想中重點強調的范圍等價性要求.以前我們接觸的大部分是直線與曲線相交,如果直線和曲線有兩個交點,消元后的方程就有兩個解;如果有一個交點,消元后的方程就只有一個實數根;如果沒有交點,消元后的方程就無解.其實是因為直線的自潔性(x確定y就跟著確定,反之也成立),所以忽略消元后范圍等價性也沒有煩惱,而這邊遇到的兩個曲線出現了一個x值對應兩個y值,麻煩就來了,消元之后的方程根的個數和交點個數并不完全對應.雖然我們的同學甲沒有做對這道題,倒是讓我們發現數學有時候并不是簡單模仿,而是一個嚴謹的思維過程,并且他幫助我們大家一起回顧了多個知識點及處理一類問題的注意事項.
最終一節課只是解決了這一個問題,但整個過程卻是和我們的一般一節課內容涵蓋量相當,所以那節課多次表揚同學甲.另外,在整個掃除障礙的過程中,我們也發現了,時到今日,就高考知識點對大家的要求而言,學生已經全部了解,所以學生有什么好的想法是很正常的,正所謂“青出于藍而勝于藍”,所以鼓勵他們多思,多總結.
后來一旦有人忽略消元后范圍等價性時,就有人開玩笑說不記得同學甲的百思不得其解了嗎,那可花了我們一節課的時間啊?比起我單純的提醒確實更有質感一點!當然不是每節課都有這樣的水到渠成,但只要有心,完全可以使復習課變得更加生動,更有效,總而言之,充分發揮學生的主體地位,教師的主導作用,對于學生和老師都是大有裨益的!
G632
B
1008-0333(2016)30-0043-02

