抓住基本圖形巧添輔助線
張瓊
抓住基本圖形巧添輔助線
張瓊
七年級同學們剛剛接觸平面幾何,難免會碰到需要添加輔助線的題目,此時,同學們普遍感覺這類題目比較難.許多同學常常會向老師提出這樣的問題:“老師,為什么要添加這條輔助線?”要解決這些問題,同學們就要掌握添加輔助線更一般的規律.
平面幾何可以通過不同圖形的不同組合而發生無窮變化,一個幾何問題,經過分析后,都一定會發現這樣一個事實:它是由一個或若干個最簡單最基本的圖形組成的,我們把這些最簡單最基本的圖形稱為基本圖形.
如圖1,已知AB∥CD.
求證:∠ABE+∠BEC+∠DCE=360°.
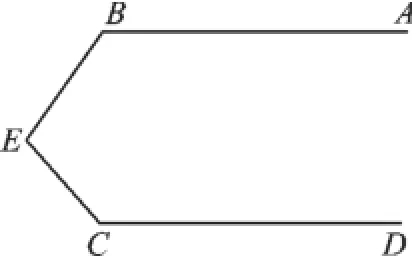
圖1
首先,學會基本圖形的識別.
人們常常感嘆于優秀生反應快,并把原因歸結為“此人天生聰穎”.實際上,優秀生之所以快,是因為他們善于將一些基本問題進行模塊化,把它們的結構和圖形儲存在腦海中,到用的時候能迅速浮現出來.這好比電腦快是因為儲存了大量的程序一樣.因此,要想做到快速識別基本圖形,平時就應當有意識地歸納和識記基本圖形.譬如要解答此題,就應當先熟練掌握“兩條平行線被第三條直線所截”的基本圖形.
本題條件中出現了一組平行線:AB∥CD,所以考慮用“兩條平行線被第三條直線所截”的基本圖形進行證明.給出的圖形中,發現基本圖形不完整,所以需要添加輔助線,根據思考規律,分為兩種情況:
①添加第三條直線;
②添加平行線.
其次,添加輔助線,構造基本圖形.
實驗組患者中有1例患者唾液增多,有1例患者失眠,不良反應發生率為12.5%;對照組患者中有1例患者唾液增多,有2例患者心動過速,有1例患者嗜睡,不良反應發生率為25.0%。實驗組明顯低于對照組,兩組差異對比具有統計學意義,P<0.05。
(一)添加第三條直線
在給出的圖形中,沒有直接與AB、CD都相交的第三條直線,所以根據這個基本圖形的思考規律,需要添加第三條直線.由于兩平行線AB、CD可能被各種位置不同的第三條直線所截,所以就會出現添加輔助線的多種可能情況.
(1)若兩平行線AB、CD被直線BC所截,由于圖中沒有直線BC,故連接BC,如圖2.
證明(略).
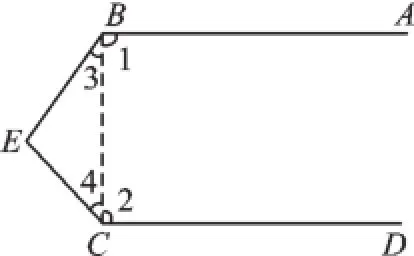
圖2
(2)若兩平行線AB、CD被直線BE(或CE)所截,由于BE與CD沒有相交,所以基本圖形不完整,故延長BE、DC交于F,如圖3.
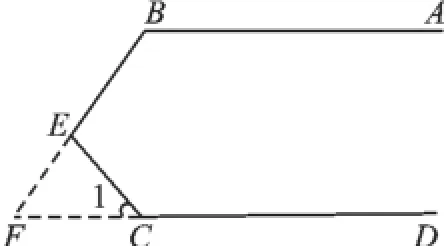
圖3
證明(略).
(3)若兩平行線AB、CD被過點C且與AB、CD相交的直線所截,則可以過點C作CF交AB于F,如圖4.
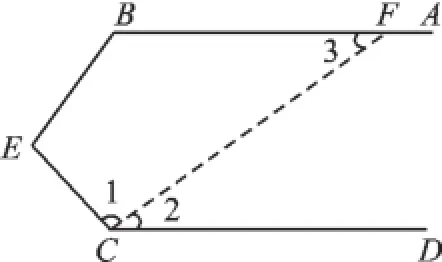
圖4
證明(略).
(二)添加平行線
若把BE(或CE)看作是截一組平行線的第三條直線,那么還缺少一條平行線,故過點E作EF∥AB.這里有兩種情況:
(4)平行線AB、CD與EF構成同旁內角,如圖5.
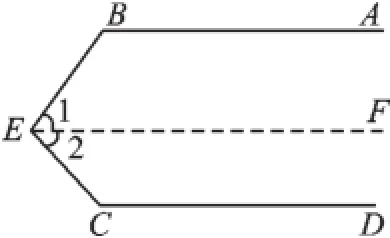
圖5
證明(略).
(5)平行線AB、CD與EF構成內錯角,如圖6.

圖6
證明(略).
第三,對添加輔助線再思考.
基本圖形的輔助線添加,首先需要根據題目條件和結論識別出基本圖形,要做到這一點,需要在做完題后,進行如下的反思:自己是怎樣想出來的?有沒有別的方法?不同的解法有沒有共同的東西?能把這個共同的東西應用于另外一些題目嗎?如果發現這個思考方法具有普遍性,那么要把它整理出來,因為這就是一個基本圖形.當我們總結的基本圖形越多,再碰到相關題目的時候,就越容易識別基本圖形,使之容易得到解決.
(作者單位:江蘇省丹陽市華南實驗學校)

