復合實物期權視角的企業R&D項目評價模擬計算

劉鳳琴，聶志平，劉利莉

（浙江財經大學 信息管理與工程學院，杭州 310018）

復合實物期權視角的企業R&D項目評價模擬計算

劉鳳琴，聶志平，劉利莉

（浙江財經大學 信息管理與工程學院，杭州 310018）

文章基于美式復合實物期權視角，運用美式期權最小二乘蒙特卡羅模擬方法對企業多階段R&D項目評價問題進行深入分析。研究結論認為，多階段多投資時點的企業R&D投資項目一般具有很強的復合實物期權特征和美式期權價值結構；實證結果表明，相對于常用的Geske兩階段評價美式期權計算模型，本文提出的評價方法具有更強的收斂穩定性。

R&D項目；跳躍擴散；復合實物期權；美式期權定價；最小二乘蒙特卡羅模擬

0 引言

R&D項目在企業決策中占據不容忽視的地位，新產品或新戰略的設計和開發往往是一個企業生存的關鍵因素，因此對R&D項目做出正確評估就成為企業投資決策的重要內容。由于R&D項目是一種平臺投資，具有彈性可調性、創造性、周期長、風險大和投資額巨大等特點，傳統方法由于忽視其靈活性會低估或錯估R&D項目價值，在80年代就陸續受到了學者們的質疑。因為期權估值理論能很好地適應管理柔性等特點，所以被認為是比較貼合R&D項目真實價值的評估方法。同時，由于R&D項目具有多階段投資的復雜性，因此，將其看作復合實物期權形式并進行定價評估更符合實際情況。

目前,學者對R&D項目進行復合實物期權模擬時多看成多階段集合形式，方法理念其實還是以Geske的兩階段模型為主。本文把蒙特卡羅模擬方法和復合實物期權理念結合起來，在多階段復合實物期權定價方案的基礎上，針對項目周期內期權執行時間重疊的情況，給出一個較完備的R&D項目估值方案。

1 R&D項目的復合實物期權特征分析

復合實物期權的內涵在于它描述了未知環境下投資決策中一系列前后緊密關聯的權利，這些權利的意義在于使決策過程更具柔性，因此復合實物期權估值方法在分析多階段序列決策問題方面有優勢。復合實物期權反映了一種全新的投資思維模式和企業戰略思想。在含有較大技術風險和市場風險的環境下制定投資策略時，復合實物期權可以賦予投資決策過程更多的選擇性。復合實物期權內會有期權交叉重疊的情況，期權間相互作用的過程也是較復雜的，Brosch R(2001)[1]通過研究實物期權的組合特性，對期權間的復合關系進行了分類和定義，把復合實物期權分為平行復合、因果復合和項目間復合。其中，平行復合應用最為廣泛，本文研究將以此為基礎來進行。

實物期權標的資產是現金流收益的現值,資產價格過程主要包括Poisson過程、Merton跳躍以及均值回復資產模型等形式。事實上,均值回復模型比幾何布朗運動更符合實際情況，尤其是跳躍均值回復模型。但在實踐中因為計算有難度，更傾向于選擇簡單模型。為此，本文將泊松跳躍資產價格模型作為基準模型，對復合實物期權定價加以分析。

假如有高新技術研發企業在T時刻有一項投資，投資與否取決于在該時刻企業的價值。若T時刻企業價值為P(T)，它是T時刻投資產生的現金流的貼現值，K為T時的投資成本。整個企業當前價值為不考慮該期權靜態NPV和該看漲期權價值之和。進一步假設如下：（1）在[0,T]期間，隨著研發工作的進行，P(T)會以指數形式穩定增長，直到有新的技術發現而產生非預期的跳躍。（2）因為競爭者的進入，這項新技術所帶來的經濟利益該企業不能完全獨占。（3）從長遠考慮，無論價值增值還是吸引競爭者進入，新技術發現產生的影響將會逐步消失。因此，項目在(0,T)時間內資產價格變化可以采用Piosson過程來描述：

在無套利和完全市場下，該看漲期權的價值為e-rTE[max(0，P-k)]。

2 復合實物期權的蒙特卡羅模擬

2.1 跳躍擴散模型的蒙特卡羅模擬

在時間區間[0,T]內，假設標的資產價格變量S(t)遵循Possion跳躍擴散過程，即：

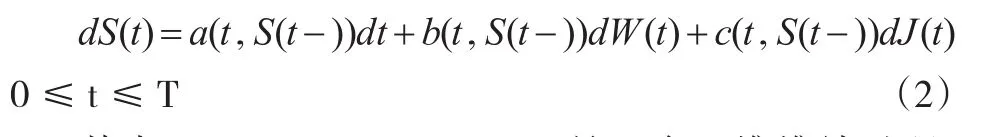
為簡單起見，假設跳躍擴散是一維泊松過程，同時跳躍強度為λ=1。利用蒙特卡洛模擬方法對資產價格進行時間離散化，如果知道初始時刻S值，根據隨機抽取的ε，則能得出Δt時刻的S值，那么2Δt時刻的值就能從Δt時刻算出來。通過N個正態分布抽樣就可以得到一個價格路徑的蒙特卡洛模擬樣本，并得到在時刻T的回報值；把這種模擬方法重復至足夠大次數，通過計算所有回報值的平均值，然后折現，就得到了期權的期望值：

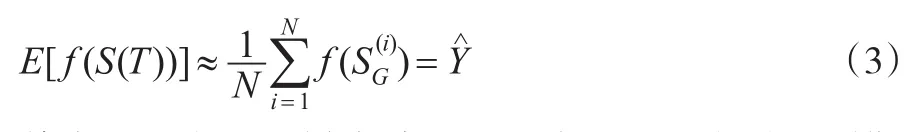
其中取N個獨立樣本路徑，SG表示S(t)在時間到期日T時的近似值。在復合實物期權中，既含有歐式實物期權類型，也含有美式期權類型。由于其前向性特點，會導致類似美式期權類型計算的不可行性，LSM方法可確定美式期權最佳執行點，從而計算美式期權價值。

2.2 美式復合實物期權定價的最小二乘蒙特卡羅模擬

根據Longstaff F A,Schwarts E S(2001)[2]，本文假設美式期權執行點是在K個離散的時間點上0＜t1≤t2≤t3≤...≤tk=T，并且在每一個離散時間點都考慮它的最佳停止策略。在期權到期日，如果美式期權是處于實值情況，那么投資者就會執行期權，反之則放棄執行。由于美式期權可提前執行特性，那么在到期日之前的tk時刻，投資者必須做出選擇，如果計算得出期權立即執行的價值要大于持有這一期權的價值，投資者毫無疑問會選擇立即執行期權。在時間點tk，選擇立即執行期權獲得現金流為已知，而繼續持有可能產生現金流卻是未知。根據無套利定價假設，持有期權價值為風險中性測度下C(ω，s;tK，T)折現后的條件期望值：

式（4）中r(ω，s)表示無風險折現率。LSM算法目標就是通過最小二乘法在時刻點tk-1，tK-2，...，t1逼近期權繼續持有的條件期望值；由于依賴樣本路徑的現金流函數C(ω，s;t，T)是由遞歸定義期權而產生，因此具有后向迭代性，需要進行后向式計算。Longstaff F A和Schwarts E S (2001)[2]研究表明，用3個基函數可獲得足夠收斂度。在計算過程中，由于投資者只會在期權價值大于零時刻執行，因此可以只考慮期權價值大于零的路徑，如此就大大減小了期望函數估計范圍。

2.3 實物期權的模型求解

本文主要分析延遲期權，其他類型期權可相應分析，假設延遲期權的延遲期為[0，T0]，延遲期權可以在延遲期內任意時間執行。在求解時，需要比較每個時間點上的立即執行期權獲得價值和繼續持有期權價值，將較大值作為該時間點上的期權價值。將[0，T0]分為N1個長度相等的時間區間，記為在To時刻，第p條路徑上的期權價值為：

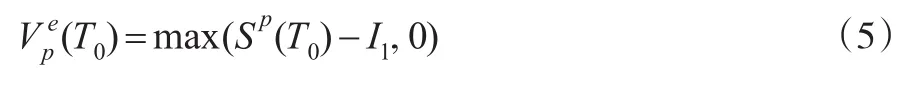
ti時點p條路徑上立即執行項目價值為-I1，步驟為：

①求得在To處的期權價值，記為，并且把每條路徑上的期權執行時間都記為

②選取tN1-1時刻所有期權執行價值大于零的路徑，設共L條，標記為p1，p2，…，pL。計算出這些路徑上繼續持有期權的價值的現值為：

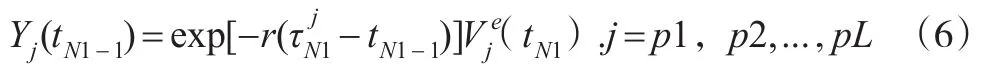
運用最小二乘法求解方程，得到a0，a1，a2的值；這里用3個基函數可以獲得足夠收斂效果。

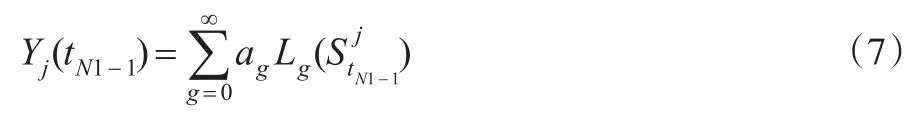
在此基礎上，運用以下方法確定每條路徑上的期權是否應該在tN1-1時刻執行。若在某條路徑上期權的立即執行價值為零，則期權肯定是繼續持有，不會執行。而在L條執行價值大于零的路徑上，利用上面LSM方法得到參數來重新計算此路徑上期權的持有價值，為：

如果計算出的持有價值大于這條路徑上此點的執行價值，期權就會繼續持有；若持有價值小于執行價值，期權將會在此點執行。記tN1-1時刻每條路徑上期權執行時間為有反之

③假定求得ti+1時刻期權在每條路徑上的執行時間為，欲確定在ti期權執行時間首先選取執行價值大于零的所有路徑，假設有L'條，標記為 p1，p2，...，pL'，計算在這些路徑上期權持有價值折現到ti時刻的價值為

求解出a0，a1，a2的值。

④計算出期權的價值為：

第一步：在[T3,T]期間運用計算轉換期權價值方法計算期權價值。首先，運用上述轉換期權價值計算式得到轉換期權在每條路徑上的價值其次，在項目擴張投資規模的情況下，運用轉換期權價值計算方法得出轉換期權在每條路徑上的價值：最后擴張期權在T3處的價值為

3 案例計算

3.1 案例描述

基于Cassimon D,Engelen P J(2010)[3]案例數據，分別給出基本現金流和成本數據以及內含復合實物期權相關數據。移動支付系統在2010年至未來時間里損益值如表1所示，2012年開始市場化推廣之后才有了現金流產生。

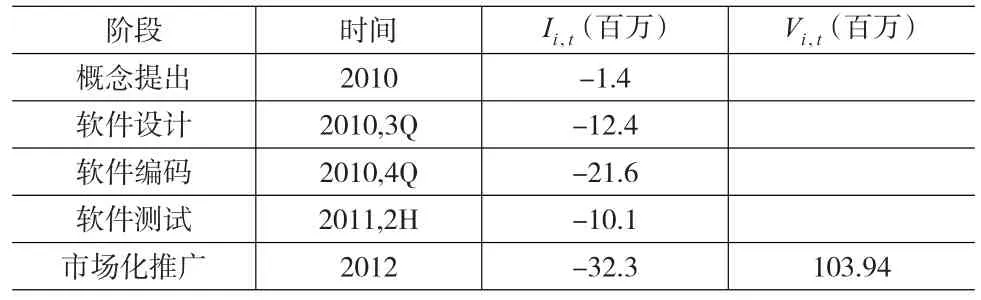
表1 移動支付系統開發損益值

其中，Ii，t表示在每一階段開始時的投資支出，Vi，t是預期現金流產生值，僅僅在進入到推廣階段時才會產生，在市場化推廣階段開始的時刻估算而得。在提出軟件開發項目商業概念之后，由于商業環境極度不明朗，管理者不會馬上進入移動支付系統開發，而是等待有利信息出現，以確定此移動支付系統有很大可能會帶來商業價值，或者避免不必要的后期投入，這就是延遲期權價值內涵。此軟件系統最遲會在T0=0.5，以投資額I1=12.4（百萬）開始移動支付系統研發。此外，延遲期權有類似于美式期權特征，投資者可以根據市場環境在T0之前的任意時間內進入到設計階段研發。在設計階段結束即將進入到編碼階段時點上，管理者可以根據移動支付系統商業前景，選擇在T1=0.8時刻是否徹底放棄移動支付系統的繼續開發；如果不放棄，則將以I2=21.6（百萬）投資額進入到軟件編碼階段的研發。

3.2 模型參數估計

模型參數主要包括波動率參數、跳躍強度λ以及跳躍值Yj等，其中關于波動率估計，主要運用Park C,Kang J M, Min B(2013)[4]里的專家咨詢評價方法；而對模型中的跳躍強度λ以及跳躍值服從的正態分布函數參數運用MCMC方法加以解決。

3.2.1 波動率σ估計

專家咨詢評價方法是將專家小組的主觀概率和對數正態累計概率相結合，得出最佳波動率估值。采用階段波動率法，需將此波動率的范圍分為四個區間值，分別是第一階段波動率取值范圍為50%～60%，接下來的三個階段依次為38%～48%，35%～45%以及32%～42%。可以看到四階段波動率估值也大致落在32%～60%之間。因為本文對參數波動率的處理方法是分階段取值的，根據Richard和Shockley(2007)[5]方法，得出有關波動率數據如表2所示。第四列Ii表示每階段投入成本，S0表示預期現金流折現到初始時刻的值，折現率r是5.32%，采用的是2012年發行的3A級五年期國債利率近似作為無風險貼現因子。

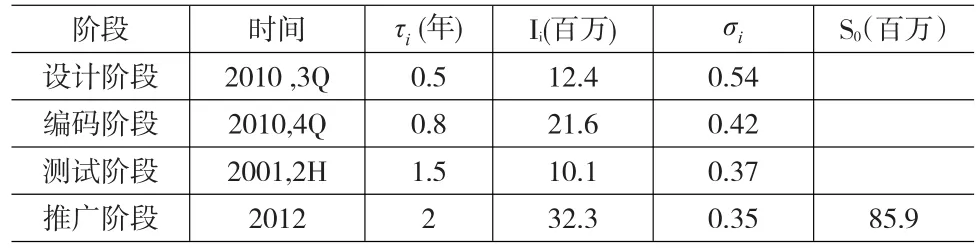
表2 軟件開發項目案例數據及波動率估計

3.2.2 MCMC參數估計

根據軟件開發項目實際數據可得，資產價格初始值為S0=85.9（百萬）；運用蒙特卡羅模擬方法，得出資產價格歷史軌跡。其中，模型參數部分運用歷史數據來運算，再從中選取一部分資產價格數據，作為參數估計輸入數據。根據資產價格模擬過程的MATLAB程序運行所得數據，選取其中60組數據，每兩個取平均值，作為MCMC參數估計方法中S0的基準數據。MCMC方法各個參數先驗分布值來源于劉昭文（2011）里相同參數先驗分布，即：λ～Beta(2，100)，Yj～N（ψ，γ2）中，期望和方差的先驗分布為1/γ2～IGa(2.5，0.025)。根據MCMC方法估值步驟，人工迭代4000次，可得到各個參數路徑迭代軌跡以及后驗分布，參數估計相關指標如表3所示：

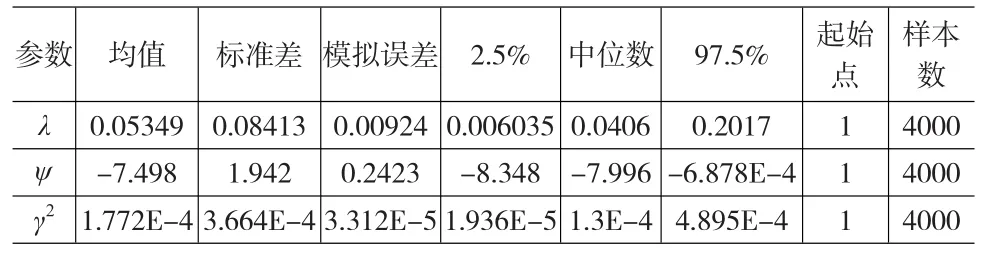
表3 模型參數統計結果

從表3可以得到：λ=0.05349，ψ=-7.498，γ2=1.772E-4，并可得：μ0=5.5419E-4。則：

其中Yj～N（-7.498，1.772E-4）,Nt為 λ=0.05349的泊松分布，初始值S0=85.9（百萬）。

3.3 復合實物期權價值模擬

第一步：利用最小二乘蒙特卡羅模擬方法，運用MATLAB計算軟件，分別模擬出了1000次至10000次中的10次均值結果，圖1描述了延遲期權價值隨模擬次數變化的軌跡，取模擬4000次的MATLAB運算結果，可以得到Vp(tT3/Δt)=70.38（百萬）。

圖1 延遲期權模擬值變化曲線

在時間區間[T3,T]即[2.5,7]年內，擴張投資情況下，計算出2.5年時刻轉換期權價值在擴張投資情況下，在2.5年時點項目初始價值變為86.6（1+e）=115.2(百萬)。用MATLAB程序計算可得到2.5年時刻的轉換期權的價值取4000次程序計算結果可得出2.5年時刻的轉換期權的價值=128.7（百萬），運用最小二乘法得到的項目收縮且擴張下第2.5年時點處的期權價值模擬結果如圖2所示。

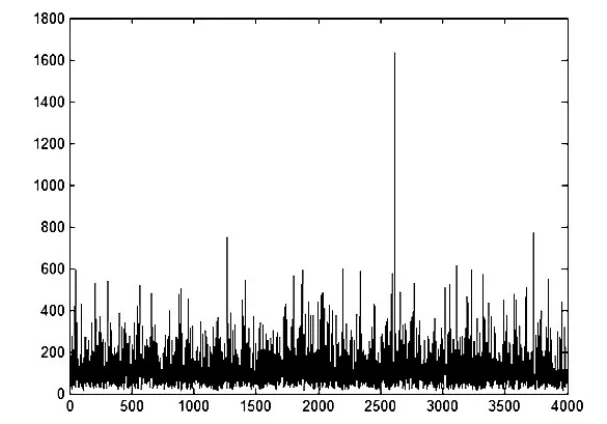
圖2 項目收縮且擴張下第2.5年時點處的期權價值模擬圖

第二步：擴張投資和不擴張投資期權價值的計算區別在于標的資產的計算公式和初始投資值的不同，若在2.5年時擴張投資，則資產價格在此刻的初始值將改變，得到2.5年時刻擴張期權價值為：

在時間區間[T′2，T3]即[2,2.5]年內，同樣運用計算轉換期權價值公式算出在2年時點的轉換期權價值，通過程序計算可得到結果為110.5（百萬）。利用以上計算結果減去第2年時的初始投資，也就是在收縮投資的情況下，轉換期權價值為：

將此值以無風險利率r=0.052折現到T2=1.5年末再減去測試階段的初始投資，同時將收縮投資額考慮進去，便得到軟件開發項目收縮投資情況下期權價值，記為

第三步：在項目不收縮投資情況下，計算出1.5年末項目的期權價值。步驟與第二步一樣。同樣把1.5年時此軟件開發項目在不收縮投資情況下的期權價值記為Vp(tT2/Δt)-I3。運用第二步中同樣的計算步驟可得到最終的不收縮情況下第1.5年時點的期權價值Vp(tT2/Δt)-I3= 88.7（百萬）。

第四步：比較第二步和第三步的計算結果，得出1.5年時點收縮期權的價值。記為即可得到此軟件開發項目在第

1.5年時點的收縮期權的價值為88.7（百萬）。

第五步：將第四步得出的收縮期權價值折現到T1=0.8年末，利用放棄期權價值計算公式來計算此時點下的放棄期權的價值：

第六步：將第五步計算而出的結果折現到T0=0.5年末，得出此點的期權價值，記

第七步：運用前述推遲期權價值計算方法中第一步至第三步的方法確定出推遲期權在每條路徑上的最佳執行點，然后從起始時刻開始，沿著每一條路徑尋找出第一個最佳執行點，將此點的期權價值折現到起始時刻，得出每條路徑上起始時刻推遲期權的價值，對所有路徑上得出的期權價值V″

p取平均值，便得出此軟件開發項目復合實物期權總價值。

對最后的結果取模擬4000次下的平均值，得到推遲期權的價值為38.64（百萬），也是整個復合實物期權的價值，再減去軟件開發項目起初的概念投資I0=1.4，可以得到最終的項目價值為37.54(百萬)。

4 結論

本文針對傳統估值方法的缺陷，運用復合實物期權理論，并借助蒙特卡羅模擬數值解法重新探究了R&D項目的價值評估問題，研究結論歸納為：

（1）由于R&D投資項目是階段性投資，同時具有多個投資時點，因此復合實物期權更適合分析其價值結構和估值計算問題。

（2）雖然實物期權理論來源于金融期權，但其傳統金融解析方法不再適用于實物期權求解，數值解法會更先進方便，通過借助MATLAB等模擬軟件，可以得出較準確的結果。

（3）在實證分析中，對波動率和跳躍因子的參數估計做了詳細的分析，結果得出，對于風險性較大，投資階段性特征明顯的R&D項目，運用復合實物期權思想，并采用解析方法，可以得出更靈活、更貼合真實價值的評估結果。

[1]Brosch R.Portfolio-aspects in Real Options Management[J].Plant Cell Reports,2001,15(12).

[2]Longstaff F A,Schwarts E S.Valuing American Options by Simula?tion:A Simple Least-Squares Approach[J].The Review of Financial Studies,2001,14(1).

[3]Cassimon D,Engelen P J,Yordanov V.Compound Real Option Valua?tion With Phase-Specific Volatility:A Multi-phase Mobile Payments Case Study[J].Technovation,2010(31).

[4]Park C,Kang J M,Min B.Compound Real Options Incorporated With a Stochastic Approach for Evaluating an Uncertainty in Petroleum Ex?ploration[J].Energy Sources,2013,PartB:Economics,Planning,and Pol?icy,8(3).

[5]Richard L.,Shockley Jr.A Real Option in a Jet Engine Maintenance Contract[J].Journal of Applied Corporate Finance,2007,19(2).

（責任編輯/劉柳青）

F273

A

1002-6487（2016）23-0166-04

國家自然科學基金資助項目（71271190）；教育部人文社會科學研究項目（15JYA630037）

劉鳳琴(1966—)，女，浙江杭州人，博士，副教授，研究方向：金融工程與金融管理。