不同的問題同一個模型

不同的問題同一個模型

李兆龍

從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，求出結果并討論結果的意義.這些內容的學習有助于初步形成模型思想，提高學習數學的興趣和應用意識.

例1一個轉盤被分成2個半圓，分別標為A、B.甲、乙2人玩轉盤游戲，規則如下：轉動轉盤2次，當轉盤停止運動時，如果指針指向相同的字母，那么甲得1分，如果指針指向不同的字母，那么乙得1分.做10次這樣的游戲，得分高的為贏家.你認為這個游戲規則對雙方公平嗎？為什么？

【解析】P（指針指向相同的字母）=，P（指針指向不同的字母）=，游戲規則對雙方是公平的.

【反思】這個游戲與“拋硬幣游戲：拋擲1枚質地均勻的硬幣2次，如果2次都出現正面朝上或反面朝上，那么甲得1分，否則乙得1分”是同一個概率模型.

【模型應用】甲、乙、丙三位同學打乒乓球，想通過“手心手背”游戲來決定其中哪兩個人先打，規則如下：三個人同時各用一只手隨機出示手心或手背，若只有兩個人手勢相同（都是手心或都是手背），則這兩人先打，若三人手勢相同，則重新決定.那么通過一次“手心手背”游戲能決定甲打乒乓球的概率是.

【解析】首先根據題意畫出樹狀圖，然后由樹狀圖求得所有等可能的結果與通過一次“手心手背”游戲能決定甲打乒乓球的情況，再利用概率公式即可求得答案.分別用A、B表示手心、手背.畫樹狀圖得：

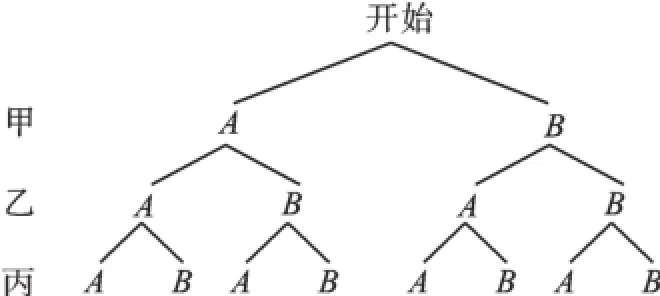
∵共有8種等可……