撥開云霧見晴天
——統計與概率生活應用題解析

撥開云霧見晴天
——統計與概率生活應用題解析

朱呈霞

親愛的同學們，你們好！經過一段時間的學習，你們應用數學解決難題的能力是不是又增強了呢？筆者前兩天遇到幾個問題，此刻的你可以幫助解決嗎？

問題1學校準備從甲、乙兩位選手中選擇一人代表學校參加所在地區的漢字聽寫大賽，學校對兩位選手從表達能力、閱讀理解、綜合素質和漢字聽寫四個方面做了測試，他們各自的成績（百分制）如下表：

選手甲乙表達能力8 5 7 3閱讀理解7 8 8 0綜合素質8 5 8 2漢字聽寫7 3 8 3

（1）由表中成績已算得甲的平均成績為80.25，請計算乙的平均成績，從他們的這一成績看，應選派誰;

（2）如果表達能力、閱讀理解、綜合素質和漢字聽寫分別賦予它們2、1、3和4的權，請分別計算兩名選手的平均成績，從他們的這一成績看，應選派誰.

聰明如你，一定已經想到解決的辦法了吧？咱們一起來交流一下吧.

【分析】（1）中根據乙的四個方面的成績，我們很容易算得他的平均成績：

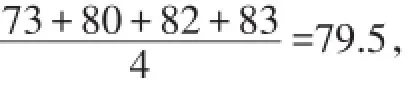
∵80.25＞79.5，

∴應選派甲.

（2）中由于四個方面賦予的權重不同，所以我們看到同樣數據在這個條件下得到的平均值與（1）中不同.

甲的平均成績：

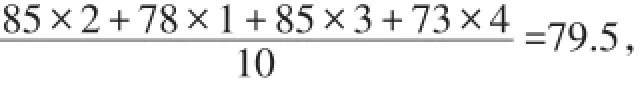
乙的平均成績：

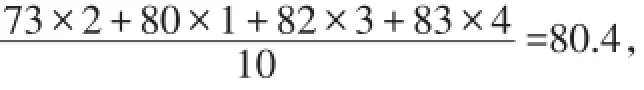
∵80.4＞79.5，∴應選派乙.

同學們，在上述這道問題中，我們要正確地解決，就需要用到所學過的統計知識.其中，我們主要用到了平均值來幫助我們進行判斷.當然，除此以外，統計知識中還涉及中位數、眾數、極差、方差、標準差以及統計圖表的相關應用.

下面，咱們再來看一道題目.

問題2為聲援揚州“運河申遺”，某校舉辦了一次運河知識競賽，滿分10分，學生得分為整數，成績達到6分以上（包括6分）為合格，達到9分以上（包含9分）為優秀.這次競賽中甲、乙兩組學生成績分布的條形統計圖如圖所示.

（1）補充完成下面的成績統計分析表：

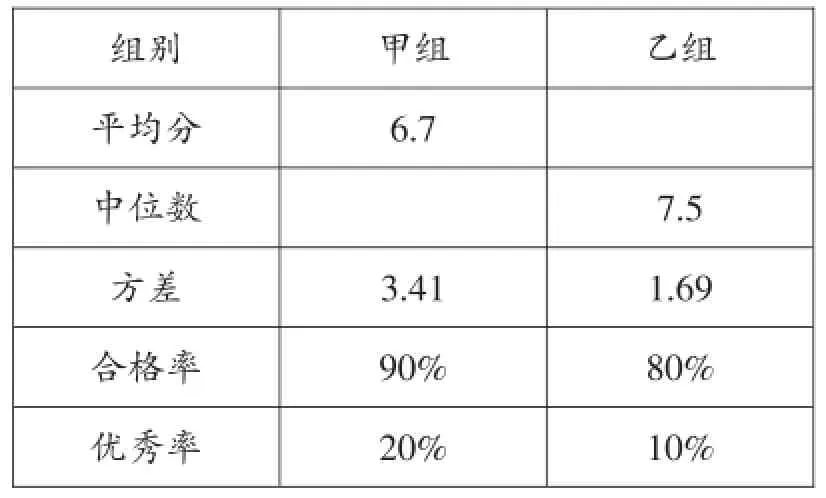
組別平均分中位數方差合格率優秀率甲組6 . 7乙組3 . 4 1 9 0 % 2 0 % 7 . 5 1 . 6 9 8 0 % 1 0 %

（2）小明同學說：“這次競賽我得了7分，在我們小組中排名屬中游略偏上！”觀察上表可知，小明是組的學生；（填“甲”或“乙”）

（3）甲組同學說他們組的合格率、優秀率均高于乙組，所以他們組的成績好于乙組.但乙組同學不同意甲組同學的說法，認為他們組的成績要好于甲組.請你給出兩條支持乙組同學觀點的理由.

【分析】（1）通過對條形統計圖的觀察和分析，我們得到甲組的成績為3，6，6，6，6，6，7，8，9，10，甲組成績的中位數是6分；乙組的成績為5，5，6，7，7，8，8，8，8，9，平均分為×（5+5+6+7+7+8+8+8+8+9）=7.1分.完成表格.

（2）觀察上表可知，小明是甲組的學生.

（3）①乙組同學成績的平均分高于甲組；②乙組同學成績的方差比甲組小，成績穩定，而且集中在中上游.

通過上述兩題，同學們是否發現，統計知識在我們的生活中起著非常大的作用呢！它可以幫助我們對現有收集到的數據進行分析和處理，弄清事物發展的動態和趨勢，從而做出正確的判斷.

當然，有的時候，我們不光要能夠運用統計的知識整理和分析數據，得出結論，還要進一步根據樣本數據估算總體的情況，另外，還要能夠確定不同情況下事件發生的概率.

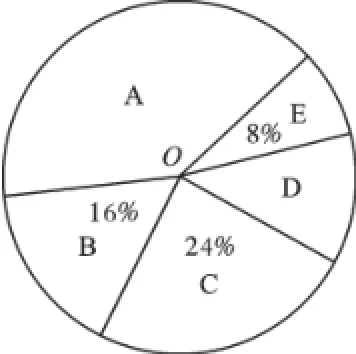
問題3泰州市為進一步加強和改進學校體育工作，切實提高學生體質健康水平，決定推進“一校一球隊、一級一專項、一人一技能”活動計劃.某校決定對學生感興趣的球類項目（A：足球，B：籃球，C：排球，D：羽毛球，E：乒乓球）進行問卷調查，學生可根據自己的喜好選修一門，李老師對某班全班同學的選課情況進行統計后，制成了兩幅不完整的統計圖（如圖）.

（1）求出該班學生人數；

（2）將統計圖補充完整；

（3）若該校共有學生3500名，請估計有多少人選修足球？

（4）該班班委5人中，1人選修籃球，3人選修足球，1人選修排球，李老師要從這5人中任選2人了解他們對體育選修課的看法，請你用列表或畫樹狀圖的方法，求選出的2人恰好1人選修籃球、1人選修足球的概率.

【分析】（1）用B的人數8除以所占百分比16%得出班級總人數50.

（2）用D的人數6除以50得D所占的百分比12%，1-16%-24%-12%-8%=40%，即為A的百分比；50分別去乘A、C、E的百分比即得各組的人數，補圖即可.

（4）列表即可求得概率.用“1”代表籃球，“2、3、4”代表足球，“5”代表排球，可以用下表列舉出所有可能出現的結果.

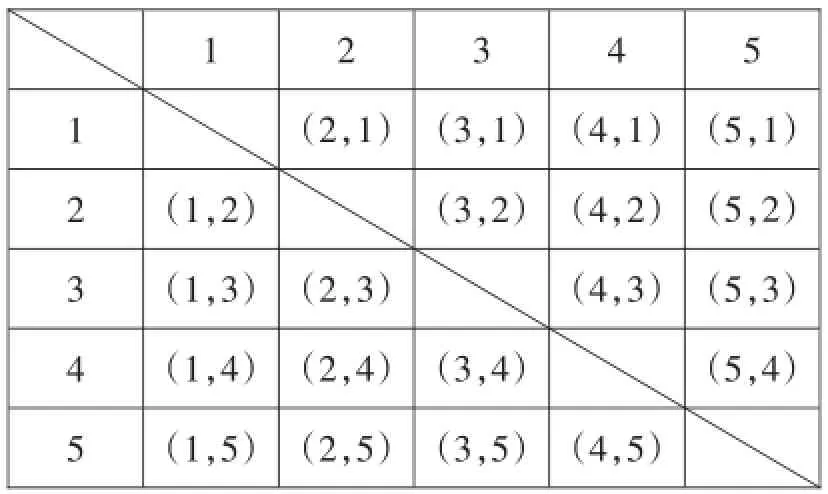
1 2 3 5（2，1）（2，3）（2，4）（2，5）1 2 3 4 5（1，2）（1，3）（1，4）（1，5）（3，4）（3，5）（4，5）（4，1）（4，2）（4，3）4（3，1）（3，2）（5，1）（5，2）（5，3）（5，4）

由圖可以看出，可能出現的結果有20種，并且它們出現的可能性相等.選出的兩人1人選修籃球、1人選修足球（記為事件A）的結果有6種，即（1，2），（1，3），（1，4），（2，1），（3，1），（4，1），所以P（A）=

生活離不開數學，數學離不開生活，數學知識源于生活而高于生活，最終服務于生活.而概率統計正是在生產和生活實際中通過不斷總結和提煉而形成的數學手段和方法，對實際生活有著指導和應用的價值與功能.在解決實際生活中的問題時，我們應當具備用所學的知識解決實際問題的能力.

同學們，通過上述問題的解決，你們對統計概率的知識在實際生活中的應用是不是又有了更深的認識呢？祝你們學習愉快！

（作者單位：江蘇省淮安外國語學校）