淺談小學數學課堂錯誤資源的合理利用

王 瀅

（吉林省柳河縣紅石鎮紅石小學 吉林柳河 135300）

淺談小學數學課堂錯誤資源的合理利用

王 瀅

（吉林省柳河縣紅石鎮紅石小學 吉林柳河 135300）

錯誤是指叫教師在教學中和學生在學習中，反映在各方面的必然產物，學生的認知水平、知識背景、思維方式、情感體驗、表達形式各不相同，他們在學習過程中出現各種各樣的錯誤是十分正常的。

小學數學課堂 錯誤資源 合理利用

教師要針對學生在數學課堂教學中出現的不同錯誤，研究各種錯誤的成因，利用學生的錯誤資源，提高課堂教學效率，同時更要提高教師捕捉并利用學生的錯誤資源的能力，提高教師對教材和課堂的駕馭能力，使學生在錯誤中成長，進而培養學生批判性的數學思維品質，突破思維性的干擾。讓教師在研究學生的錯誤資源中成長，提高教師的專業水平。

一、利用“錯誤資源”，豐富我們對教學內容的選擇

在教學中，面對學生的錯誤，我們經常不屑一顧，這種做法，既使得我們與學生之間產生隔閡，又使得學生的錯誤難以徹底解決。如果我們反其道而行之，在教學時，直面學生的錯誤，并將學生的錯誤作為一個教學資源，作為一個教學的原點，讓學生在與這些錯誤碰撞中，讓學生在這些錯誤的思辨中，領略到數學的實質內涵，學生一定會受益匪淺。

例如關于“小數精確值與保留位數”的教學內容選擇

在小數的知識體系里，“保留小數點后的數位”是小數精確值的一個重要體現，但這一知識卻是學生經常出錯的且難以理解的內容。如果我們還是按照教材安排的，從“精確值”到“保留數位”進行教學，是很難引起學生的共鳴的。為此我在教學時，拋棄教材中的關于“精確值與保留數位”的內容，基于學生的錯誤，并將其擴大化，從而讓學生獲得有關“精確值與保留數位”的內容的深刻認識。如一位學生在計算時直接把“4.0”寫成“4”，盡管這兩個數值的大小結果是一樣的，但它們所表示的精確值卻是完全不一樣的。因為這個“0”去掉后，它就只能精確到個位，如果保留，那它的精確程度就是十分位。此時我便針對學生的錯誤，畫出一個數軸圖，幫助學生直面錯誤的根源。當我們將“4.0”寫成“4”后，根據“四舍五入”的原則，它的取值范圍就是“3.5”到“4.4”之間，顯然這與“4.0”的取值范圍是不一樣的——“4.0”的取值范圍是“3.95”到“4.04”之間。但我們引導學生直面錯誤，并將其擴大、顯化，學生會在錯誤中理清知識的來龍去脈，會在錯誤中尋找到自己的失誤根源。

二、利用“錯誤資源”，促進有效生成

可以這樣說只要有認知活動就有錯誤的發生，學生在數學課堂中的學習也是一樣。在教學中，學生常常有錯誤出現，往往與教師的預設不合拍，讓教師出乎意料。而這些課堂現象，恰恰潛藏著生長性和生成性，是值得珍惜的教學資源。

在《確定位置》的教學中，我教完數對表示位置后告訴學生用數對（4，3）表示位置非常簡潔，一目了然，隨后準備講解數對（4，3）各個要素的意義時，一個學生說：老師，我可以用4—3或4.3來表示數對嗎?我認為這樣更簡潔。

這雖然是一個意外，但卻是一個極具價值的錯誤想法。

我肯定了他的想法很有創意，表示也更加簡單，并對這名學生說：“你能說說用4—3或4.3表示位置的意思嗎？”

學生回答：“4表示列、3表示行，--或.表示隔開的意思。”

我又追問：“同學們，討論一下，能不能用剛才那個同學的形式來表示數對？”

學生經過討論后發現：4—3容易和門牌號碼混淆，4.3容易和小數混淆。

接著在與正確數對（4，3）的比較中，學生不但明白了數對表示有講究，更有專門的表示方法，并在自主交流中明白了該數對中4表示列，3表示行，“，”表示隔開，（）表示合在一起表示相交的點等內在含義。

這樣一個錯誤的想法，卻孕育著創新的思維。教師的有效捕捉，不但讓錯誤成為一個研究素材，成為有效學習的資源，更成為學生進一步學習的重要突破口。

三、利用“錯誤資源”，在對比分析中獲得方法

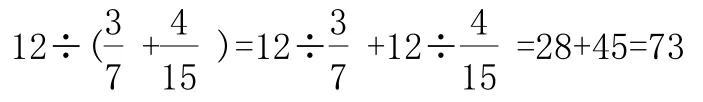
對此我并沒有說對錯，而是出示了：16÷（1+2）讓學生計算。學生逗樂了：老師這么簡單的題還用計算嗎？我追問道：還可以應用什么定律來進行計算？學生躍躍欲試，猶豫不決后還是放下了。最后我說，有的同學是這樣計算的：18÷1+18÷2=18+9=27。教室里一片笑聲。我引導學生進行比較和

在交流中一位同學指明：A×（B+C）=A×B+A×C，但是A÷（B+C）≠A÷B+A÷C。這里學生出錯是受乘法分配律的影響，習慣性地去掉括號，被除數分別括號中的兩個數，自認為這樣計算簡便些。這些其實是由于學生思維定式引起的干擾性錯誤，是學習上的負遷移。因此在教學簡便運算時候，最好讓學生理解算理，呈現給學生的應是對比練習題，讓學生知道有些習題通過定律運算簡便，有些是不能夠進行簡算的，只有這樣讓學生通過對比練習理解算理，從而更好地掌握簡便的計算方法。

四、利用“錯誤資源”，進行思維教育

在教學“倒數的認識”后，我出示一組求倒數的填空題，幾分鐘后將一名學生的作業投影到大屏幕上。具體如下：

3. 1的倒數是（1） 4、0的倒數是（0）

我問：這位同學的答案正確嗎？學生齊聲回答：正確！

我又問：真的一道也沒有錯？ 學生回答：的確沒有！

我說：請同學們根據倒數的意義，用“因為A×B=1，所以A與B互為倒數”的句式把這幾道題讀一遍。

我問：怎么不往下讀了？學生說：不對！0×0≠1，所以0的倒數不是0。我問：那么0的倒數應該是幾呢？學生陷入思考中，這時有一名學生說：我認為0的倒數還應該是0。因為0寫成分數是-把倒過來是-我繼續問：你們同意這位同學的觀點嗎？這時又有一位同學發言：我不同意！根據 商×除數=被除數，假如1÷0=0，0×0不就等于1了嗎？所以0的倒數找不到的……啊，老師你騙了我們……

上述教學，教師將錯誤資源融合在新知識的鞏固中，及時對學生進行了一次邏輯思維訓練。使學生的認知結構得到了重組。