電力系統最近負荷邊界的計算方法

衣 濤，王承民，謝 寧

（上海交通大學電子信息與電氣工程學院，上海 200240）

電力系統最近負荷邊界的計算方法

衣 濤，王承民，謝 寧

（上海交通大學電子信息與電氣工程學院，上海 200240）

確定電力系統最近的負荷邊界點對研究系統的靜態穩定有著重要的意義。本文以節點電壓和支路電流為狀態變量的混合電力網絡方程為研究基礎，建立了代表系統穩定邊界的特征方程，明確了在電壓靜態穩定臨界圓上的邊界條件。通過幾何分析找到負荷點與對應的穩定邊界的最近距離方程，建立了最小負荷邊界的附加方程形成求解方程組，方程組采用牛頓迭代算法求解，為了避免在負荷邊界附近雅可比矩陣奇異，算法采用了對雅可比矩陣中臨界點替代的方法進行計算。仿真計算結果表明，該方法是正確的和有效的。

負荷邊界；特征方程；潮流計算；電力系統；雅可比矩陣

隨著可再生能源發電的大規模接入電網，其不確定性給電網帶來了不小的沖擊，并且隨著電力系統規模越來越龐大，電力系統的運行狀態變得越來越復雜。在重負荷情況下，擾動造成的電網故障更容易大范圍蔓延，甚至導致電壓崩潰事故。因此，迫切需要對系統靜態穩定性進行分析，找到系統存在的薄弱環節，有針對性地進行預防。

為了評估系統靜態穩定性，學者提出了多種方法進行分析。尋找系統最近負荷邊界進而求得最小負荷裕度被普遍認為是衡量靜態穩定的有效手段[1]。目前對于最近負荷邊界的求解大致有以下幾種方法：①直接求解的方法[2]，先給定某一負荷增長方向，采用連續潮流法或零特征根法求得該負荷增長方向上的臨界點，確定負荷增長方向；②基于優化的方法[3]，通過在直角坐標系中建立電力系統最優潮流問題的二階模型，采用內點法或零特征根法求得該負荷增長方向上的臨界點；③進化算法，采用進化算法對電壓穩定邊界進行求解[4]。采用遺傳算法或遺傳算法與人工神經網絡相結合將問題轉化為優化問題[5]。

以上幾種求解方法中，第1種容易落入局部最優解中，后兩種在形式上對于解決負荷最小增長方向的問題有很大的吸引力，但算法求解是難點。本文提出了一種系統最近負荷邊界求解模型，并且定義了系統最近負荷邊界特征方程。在此基礎上，推導出最近負荷邊界的距離方程，得到系統最近負荷邊界。

1 節點電壓-支路電流為變量表示的電力網絡方程

在直角坐標系下，當忽略對地支路電導時，電力網絡可以描述為支路電流-節點電壓方程混合的形式，如式（1）、（2）所示[6]，對于支路l有

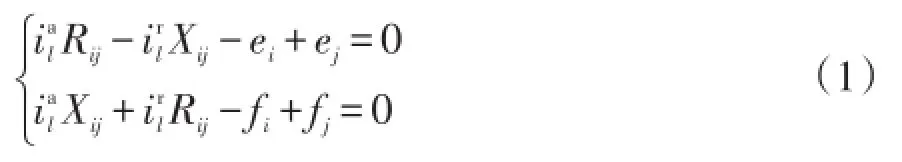
對于節點i有

式中：l=1,2,…,L，L表示支路集合；i,j=1,2,…,N，N為節點集合；分別為支路l電流的實部和虛部；ei、fi為節點i電壓的實部和虛部；Rij、Xij分別為支路l的電阻和電抗；Bl為支路l對地的1/2電納；pi、qi為節點注入的有功和無功功率。對于節點 j有同樣形式的方程。令分別表示節點注入電流的實部和虛部（不含對地支路電流）；

由文獻[6]可知，通過對式（1）、（2）的推導，可得PQ節點電壓表達式為

式中bil是節點i相關聯的支路對地電納之和。

由式（3）得到方程有解的邊界特征方程為

當滿足條件（4）時，PQ節點電壓變為

2 代表系統最小負荷裕度的距離方程

從平面幾何分析的角度不難證明，經過圓外一點與圓心相連的直線與圓相交于兩點，那么圓外點與這兩點的連線代表了圓外點與圓的距離的最大值和最小值。當這個圓是電壓不穩定圓時，這個距離的最小值就代表了最小的負荷裕度。如圖1所示，當電壓不穩定圓外任一點b與圓心連線和圓邊界相交于a、c兩點，a、c是節點b對應圓上的臨界點。此時，過a和c點圓的切線l1和l2與過原點和a、b、c點的法線是垂直的，l1與l2是平行的。b點與圓相交的最近距離的點是a點，最遠距離為c點。因此，如果已知l1、l2、l3方程，通過互相垂直的關系，可以得到負荷點b與點a的距離方程，代表著圓外節點b與圓的最近距離。

圖1 最小負荷距離Fig.1 Minimum load distance

由式（4）可得過圓上的點a和c的切線l1、l2方程為

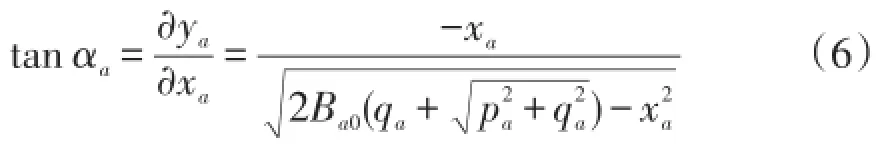
式中 βb為過點a、b、c和原點的法線角度。因為αa=βb+90°，對于PQ節點可得其距離方程為

式中：αa為過圓上a或c點的切線的角度；xa,ya分別表示a點注入電流的實部和虛部；Ba0為與a點相關聯的支路對地電納之和；pa,qa為a點注入的有功和無功功率。法線l3方程為

式中yb和xb可由式（1）確定，則代表了系統最小的負荷裕度。

3 算法求解

去除節點電壓方程中使雅可比矩陣奇異的節點b，直接使用負荷邊界上的節點電壓表達式（5），此時節點電壓方程降低一維。式（1）、（2）形成電力網絡方程，式（4）、（5）、（8）形成負荷邊界點的邊界特征方程以及距離方程。此兩組方程聯立可求解最近負荷邊界。

根據計算得到pa、qa，則

式中Sa或Pa表示負荷邊界的參數條件，表示節點b所對應的靜態電壓穩定的邊界。在求解出點a的pa和qa后，節點b的負荷最小的變化方向由式（10）確定，即

式中δb為節點b變化的角度。最小負荷邊界距離由歐式距離來確定，即

求解出的點有兩解，分別代表最近距離點a和最遠距離點c，由ηb進行判斷得出最小解。

計算步驟如下：對于給定的網絡，由式（1）計算出yb和xb；給定節點電壓ui和支路電流il的初值；對于待求的臨界點a，采用式（1）、（2）、（4）、（5）和（8）形成以節點電壓和支路電流為變量的迭代方程，形成降低一維的雅可比矩陣，應用牛頓法進行迭代求解。

根據計算出的臨界點a的值，由式（10）和（11）計算系統最小負荷裕度的方向和大小，同時可以根據式（9）計算系統負荷邊界條件。

4 算例

以IEEE118節點系統為例進行驗證，平衡節點69和節點118對調，計算采用標幺值。計算的迭代次數為3次，收斂精度為4.878 406×10-7，迭代的收斂性和收斂精度并沒有因為支路電流的引入而變得惡劣，主要是因為描述網絡狀態的信息更加豐富了。表1為系統節點對于負荷邊界的最小負荷裕度的計算結果。表1選取了有代表性的計算結果。

從表1可以看出，對于系統中不同的節點都可以求出其負荷邊界點，進而求出節點最小負荷裕度的大小和方向。但節點之間的負荷裕度還是有所差別的。如節點59的最小負荷裕度相對較小，而類似節點108大一些，這主要是因為節點59的負荷初值比較大，而其又位于重負荷區域，導致其負荷臨界點的功率值相對較小，因此節點59與電壓臨界圓的距離比較近，所以負荷裕度小。而反之節點108的負荷裕度就大一些。

表1 IEEE118節點系統計算結果Tab.1 Calculation results of IEEE 118-node system

表2為本文方法與連續潮流法和遺傳算法在求取最小負荷邊界距離過程中的結果比較，以節點21為例，從計算結果可以看出，采用本文方法計算得出的最小負荷邊界距離為2.416，要小于連續潮流法和遺傳算法，因此計算結果說明本文方法的計算結果更接近負荷邊界。

表2 本文方法與其他方法的比較Tab.2 Comparison between the proposed algorithm and other algorithms

5 結論

（1）本文提出的方法可以應用到最小負荷邊界的計算中，分析靜態穩定邊界裕度；

（2）節點負荷的初始條件以及所在區域的負荷密度對負荷邊界距離都有影響，在調整過程中應該綜合考慮各方面的因素；

（3）系統平衡解方程和負荷邊界方程直觀地表達了系統電壓穩定的臨界條件，可以應用到電力系統其他領域的分析中。

[1]陳得治，張伯明（Chen Dezhi，Zhang Boming）.一種計算最小負荷裕度的實用方法（A practical method for calculating minimum load power margin）[J].電力系統自動化（Automation of Electric Power Systems），2008，32（16）：1-5.

[2]盧錦玲，石少通，盧洋（Lu Jinling，Shi Shaotong，Lu Yang）.含大規模風電場的電網靜態電壓穩定性評估（Static voltage stability assessment on the grid with largescale wind farm connection）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（6）：73-80.

[3]聶永輝，肖白，劉鳳蘭（Nie Yonghui，Xiao Bai，Liu Fenglan）.電力系統最優潮流新模型及其內點法實現（New optimal power flow model and its solution by using nonlinear interior point method）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2014，26（11）：53-57.

[4]Hassim F I H，Musirin I，Rahman T K A.Voltage stability margin enhancement using evolutionary programming（EP）[C]//4th Student Conference on Research and Development，Selangor，Malaysia，2006：235-240.

[5]Razmi H，Teshnehlab M，Shayanfar H A.Neural network based on a genetic algorithm for power system loading margin estimation[J].IET Generation，Transmission& Distribution，2012，6（11）：1153-1163.

[6]李宏仲，王承民，程浩忠，等（Li Hongzhong，Wang Chengmin，Cheng Haozhong，et al）.利用回路電流和節點電壓混合分析法快速構造電壓穩定域（Fast construction of voltage stability regions using hybrid analysis method combining loop current with node voltage）[J].電網技術（Power System Technology），2005，29（8）：35-39.

關于參考文獻著錄格式

1 連續出版物

標引項順序號 作者．題名．刊名（外文刊名可縮寫，縮寫后的首字母應大寫，并省略縮寫點“．”），出版年份，卷號（期號）：起始或起止頁碼

2 專著

標引項順序號 作者．書名．版本（第1版不標注）．出版地 ：出版者，出版年.（專著中的析出文獻應注明起止頁碼）

3 論文集

標引項順序號 作者．題名．見（英文時用In）：主編.論文集名．出版地：出版者，出版年．起止頁碼

4 學位論文

標引項順序號 作者．題名：［學位論文］．保存地點：保存單位，年份

5 專利

標引項順序號 專利申請者．題名．國別，專利文獻種類，專利號．出版日期

6 技術標準

標引項順序號 起草責任者．標準代號 標準順序號—發布年 標準名稱．出版地：出版者，出版年（也可略去起草責任者、出版地、出版者和出版年）

摘編于《中國高等學校自然科學學報編排規范》（修訂版）

Calculation Method for Determining the Closest Load Boundary in Power System

YI Tao，WANG Chengmin，XIE Ning
（School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University，Shanghai 200240，China）

The determination of the closest load boundary in power system is of significance to the study of its static stability.In this paper，based on the hybrid electric network equations with node voltages and branch currents as state variables，a characteristic equation is established to describe the system stability boundary，and obtain the boundary conditions on the static voltage stability circle.The equation for the distance between the load point and load boundary is found by geometrical analysis.The equations for analyzing the closest load boundary are built，and they are solved by Newton iteration method.The critical points in Jacobian matrix are replaced to avoid the singularity around the load boundary.Simulation results demonstrate that the method is correct and effective.

load boundary；characteristic equation；power flow calculation；power system；Jacobian matrix

TM744

A

1003-8930（2016）12-0038-04

10.3969/j.issn.1003-8930.2016.12.007

衣 濤（1973—），男，博士，講師，研究方向為電力系統電壓穩定。Email：yitao4965@126.com

王承民（1969—），男，博士，教授，研究方向為電力系統穩定。Email：wangchengmin@sjtu.edu.cn

謝 寧（1973—），女，博士，副教授，研究方向為電力系統穩定。Email：xiening@sjtu.edu.cn

2014-09-12；

2016-02-25

國家自然科學基金青年科學基金資助項目（51307108）