載人登月地月轉移軌道方案綜述

彭祺擘，張海聯

（載人航天總體研究論證中心，北京100094）

載人登月地月轉移軌道方案綜述

彭祺擘，張海聯

（載人航天總體研究論證中心，北京100094）

在總結國內外月球探測地月轉移軌道研究進展與現狀的基礎上，從整體上研究了地月轉移軌道的設計模型及設計約束，分析了不同類型地月轉移軌道的特點及適用性。結合載人登月飛行任務特點，討論了可滿足載人登月任務約束的軌道類型及方案，并通過仿真計算和對比現有轉移軌道研究結論，分析了不同類型軌道的飛行時間、能量消耗、月面可達區域等特性，提出了應用建議，可為載人登月任務地月轉移軌道方案深入研究提供參考。

載人登月；地月轉移軌道；設計約束；地月平動點；自由返回軌道

1 引言

月球轉移軌道具有距離遠、時間長的特點，它的設計合理與否直接關系著載人登月工程任務實施的代價乃至成敗。因此分析地月轉移軌道的類型及其特性十分必要，可使我們了解地月轉移軌道的內在規律、某些關鍵參數的影響特點等，對載人登月工程方案的制定具有指導意義。

目前有大量文獻對地月轉移軌道進行了研究，大多是以某一特定任務為背景，建立軌道設計動力學模型，對滿足一定設計約束條件的軌道進行設計，并分析其相關特性。國外研究開始于上世紀50年代阿波羅任務前，經過半個多世紀的積累，形成了大量研究成果：例如，Penzo［1］、Dal?las［2］、Gibson［3］等基于圓錐曲線拼接模型研究了自由返回軌道的設計方法及軌道特性；Miele［4］、Schwaniger［5］、Jesick［6］等基于限制性三體模型，研究了地月轉移軌道的最優設計問題；Baoyin等［7］研究了地月拉格朗日點附近和主要星體表面的轉移軌道特性與其存在類型；Kluever等［8］對電推力情況下的地月轉移軌道燃料優化問題進行了研究。

國內地月轉移軌道研究始于20世紀90年代初。黃誠等［9］研究了動力學與運動學約束條件下的高精度軌道設計方法；郗曉寧等［10?11］利用雙二體模型，對不同類型的地月轉移軌道進行了設計和特性分析；劉林等［12?13］利用限制性三體模型對地月平動點特性進行了詳細研究，并對利用平動點轉移的軌道做了設計和分析；徐明等［14］對小推力地月低能轉移軌道進行了設計和研究；寶音賀西等［15］對載人登月不同階段的軌道問題進行了評述。

本文在借鑒國內外相關研究成果的基礎上，進一步分析不同類型地月轉移軌道的特性，主要針對載人登月任務，對滿足約束條件的軌道方案進行研究，以為實際任務軌道方案選取及載人登月地月轉移軌道深入研究提供參考。

2 地月轉移軌道設計模型

2.1 軌道設計約束

載人登月對軌道設計的要求比無人月球探測更為嚴格，因此地月轉移軌道的設計需要滿足一系列約束條件，主要有工程帶來的約束和軌道本身的約束［16］。

2.1.1 工程約束

工程約束主要包括飛行時間約束和速度增量約束。受環控生保條件限制，載人登月任務一般要求地月轉移飛行時間t不能太長；另外受飛行器能力的限制，發動機所能提供的地月轉移速度增量 Δv有限，因此軌道設計時要求滿足式（1）［17］：

其中，Tmax為地月轉移所能允許的最長飛行時間，ΔVmax表示地月轉移過程飛行器推進系統所能提供的最大速度增量。

2.1.2 軌道約束

地月轉移軌道的設計主要受飛行器近地出發軌道和月球到達軌道參數的限制。

1）近地軌道出發條件約束

受測控、發射場、運載能力等條件的約束，飛行器的地球出發軌道往往不能任意選取，會受到一些制約，主要包括軌道傾角和軌道高度約束。

受發射場位置限制，地球出發軌道傾角iE一般要大于發射場緯度?Launch，如式（2）：

考慮到軌道衰減問題及運載火箭能力限制，飛行器地月轉移出發軌道高度rE一般要滿足一定條件，如式（3）：

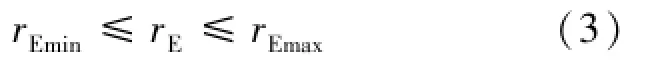
其中，rEmin與rEmax為近地出發停泊軌道允許的最小高度和最大高度。

2）環月軌道到達條件約束

因為受月面著陸點位置、月面停留時間、交會對接等的限制，要求地月轉移軌道的近月點必須滿足環月軌道參數的約束，主要包括：軌道高度約束、軌道傾角約束、升交點赤經約束［16］。

（1）軌道高度約束

要求地月轉移軌道近月點高度要大于目標環月軌道高度，又不能距離月球太遠，以便通過合適的變軌策略將航天器送入預定環月軌道，如式（4）：

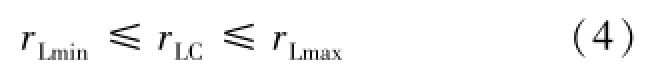
其中：rLC為地月轉移軌道的近月距，rLmin為目標環月軌道高度，rLmax為地月轉移軌道近月距允許的最大值。

（2）軌道傾角約束

為節省月面著陸的能量消耗，一般要求月面著陸器的著陸過程為共面轉移［18］，因此環月軌道的選擇必須要能夠覆蓋月面著陸區，同時受任務規模限制，載人登月一般采用環月軌道交會對接的模式，即任務完成后月面著陸器需上升與環月軌道的環月航天器完成交會對接［19］。因此，當月面活動時間較長時（幾天），則必須要對環月軌道做出合理設計，從而減少著陸器上升時與在軌環月航天器的異面差，節省上升交會燃料消耗。

由于存在應急等狀況，月面停留時間往往存在不確定性，在實際中一般設計一個最佳環月軌道，使得著陸器在月面活動期間任何時刻上升，它與環月航天器交會對接時的異面差達到最小。

以月面活動時間不大于7天為例，通過設計環月軌道傾角，使得環月交會的異面差與上升時間滿足圖1的關系［18］。

從圖中可以看出，設計的最佳環月軌道（圖中實線），雖然在月面停留7天后使得著陸器上升時與目標環月軌道的異面差最大，但與不考慮月面停留時間不確定性的環月軌道（圖中虛線）相比，其異面差峰值會大大減小，在工程實際中，只需著陸器具備這一最大異面差調整能力即可實現任意時刻上升。根據這一設計策略，下面給出最佳環月軌道傾角的求解方法。

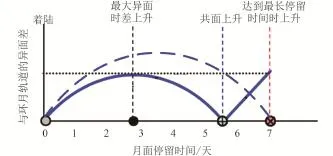
圖1 月面停留時間與環月軌道交會異面差的關系［18］Fig.1 Relationship between lunar surface stay time and magnitude of plane change wedge angle for RVD［18］

如圖2所示，設月面停留期間，著陸器與環月軌道航天器的最大異面差為W，則最佳環月軌道傾角iL、著陸點緯度?P和月面活動時間t應滿足式（5）［18］。

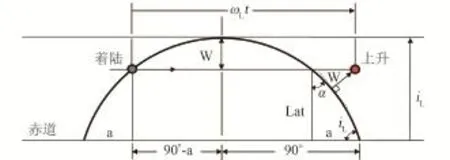
圖2 最佳環月軌道傾角與著陸點緯度的關系Fig.2 Relationship between LLO inclination and the latitude of lunar landing site

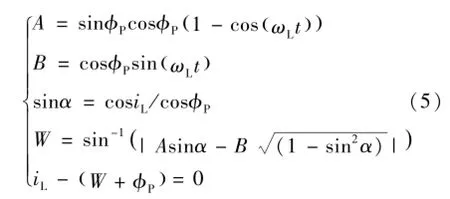
利用迭代法對上式進行求解，即可得到滿足約束的最佳環月軌道傾角。需要指出的是，這里并未考慮由于攝動導致環月軌道升交點進動帶來的影響，在實際設計中，需將此量與月球自轉疊加綜合考慮。

（3）軌道升交點約束

環月軌道在月固系下的升交點經度ΩL可根據軌道傾角和著陸點經緯度確定，設著陸點經度為λP，則有式（6）：

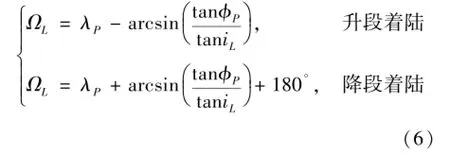
2.2 軌道設計模型

在軌道設計中，根據設計精度要求常會采用到不同的數學模型，地月轉移軌道設計最為常用的模型主要有雙二體模型、限制性三體或四體模型、高精度模型等。

2.2.1 雙二體模型

雙二體模型是研究地月飛行中常用的簡化模型，它引進引力影響球的概念，把復雜的三體問題轉化為二體問題。在雙二體假設下，地月轉移軌道分為兩段。首先是位于月球影響球之外的地心段，此段忽略月球引力，軌道為地心圓錐曲線；然后是月球影響球內的月心段，此段忽略地球引力，軌道為月心圓錐曲線；在影響球邊界上，將兩段圓錐曲線拼接為一個整體［10］。

該模型一般認為月球是繞地心作勻速圓周運動，速度約為1.018 km/s，但實際月球是繞地球作橢圓運動，軌道偏心率約0.0549。在偏心率作用下，實際地月距與該假設下的地月距最大差約20 000 km，最大速度差約60 m/s。盡管這種誤差對于地心段而言僅為飛行距離的6%左右，但對于月心段其誤差則已經超過月球影響球半徑的30%［20］，因此該模型存在較大誤差。為彌補這一缺陷，可在軌道設計過程中，將所涉及到任何時刻的月球位置和速度均以行星/月球歷表計算得到，這樣可以大大提高求解精度［21］。

2.2.2 限制性四體模型

由于飛行器的質量與地球、月球、太陽的質量相比，小到可以忽略的程度，因此，在地月轉移使命分析與初步設計中，可以應用限制性四體問題。運動方程的一般形式表示如式（7）［22］：

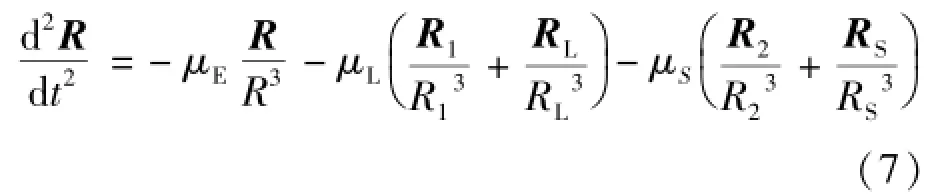
其中，R為飛行器的地心位置矢量，R1為飛行器的月心位置矢量，R2為飛行器的日心位置矢量，RL為月心的地心位置矢量，RS為日心的地心位置矢量，μE、μL、μS分別為地、月、日的引力常數。

假設地、月、日共面運動，且地月之間的距離以及太陽離地月系統質心的距離均為常量。建立地月旋轉坐標系O－xyz，原點位于地月系統的質心，x軸為地月連線，由原點指向月球方向為正方向，y軸在地月軌道平面內，由x軸逆時針旋轉90°形成，z軸與其構成右手系。取下列無量綱化單位制：長度單位為地月平均距離，質量單位為地月質量之和，時間單位為T＝P/（2π）＝3.751897869×105s，其中P為地月會合周期。在該單位系中，牛頓引力常數為1。在上述坐標系中，飛行器地月轉移的運動方程如式（8）［22］：

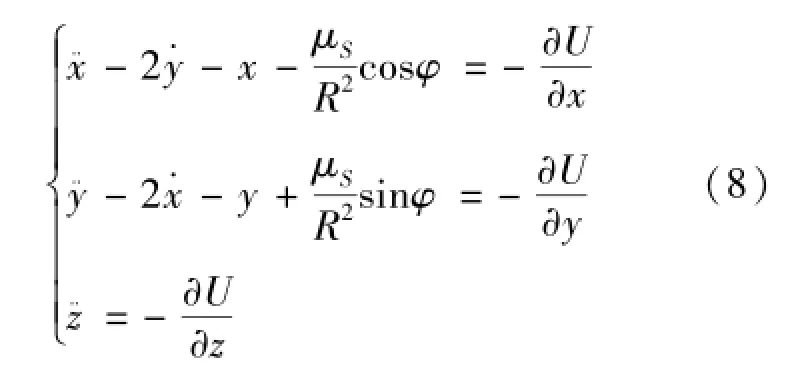
式中變量定義如式（9）：

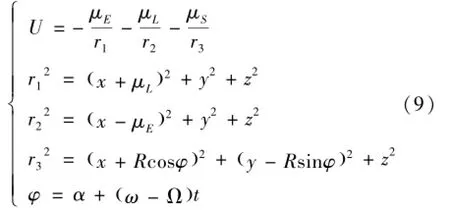
其中：ω為地球與月球繞坐標系原點的角速度；Ω為太陽繞原點的角速度；α為初始太陽方位角；R為太陽距離地月系統質心的距離。

該模型考慮了飛行器地月飛行受到的主要引力，求解精度相對較高。另外，限制性三體模型還被主要用于求解和分析地月平動點相關軌道［23］。

2.2.3 高精度模型

當計算精確的地月轉移軌道時，需要對飛行器轉移過程所受的攝動力做出分析，從而給出高精度的軌道設計模型。從軌道計算而言，飛行器的地月轉移動力學方程可以建立在地心天球坐標系下，也可以建立在月心天球坐標系下，具體計算中需要根據實際情況來選擇中心體。

當飛行器的動力學方程建立在地心天球坐標系中時，其形式如式（10）［10］：

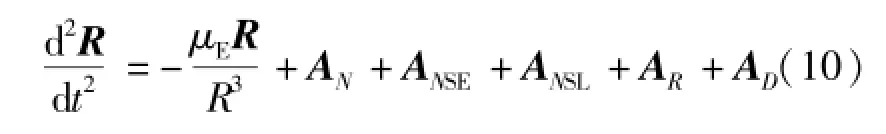
其中：AN為N體引力攝動加速度；ANSE為地球非球形攝動加速度；ANSL為月球非球形攝動加速度；AR為光壓攝動加速度；AD為大氣阻力攝動加速度。

該模型考慮了飛行器的各種受力因素，求解精度高，但計算量較大，一般在數值求解計算中采用。

3 地月轉移軌道類型

常用的地月轉移方式主要有四類：霍曼轉移方式，通過共線平動點L1走廊的轉移方式，弱穩定邊界（WSB）轉移方式和小推力轉移方式。

3.1 霍曼轉移方式

霍曼轉移方式主要是采用兩脈沖軌道機動來實現地月軌道轉移，其飛行流程大致如下：登月飛行器完成近地任務后選擇合適的時機，從近地停泊軌道出發，在出發點施加一個速度沖量，將飛行器推入奔月軌道；當到月球附近時，施加一個反向速度沖量，使其進入月球軌道（包括環月軌道或月球附近的平動點軌道），如圖3所示。

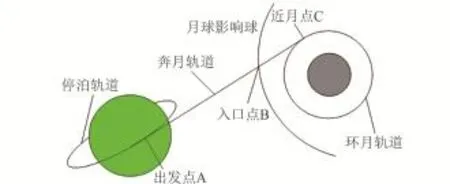
圖3 霍曼轉移方式示意圖Fig.3 Schematic diagram of Hohman transfer trajectory

采用這種類型地月轉移軌道到達月球的方式有兩種：長程到達和短程到達。長程到達是指地月飛行時間大于地月轉移地心軌道的半個周期，即到達月球時，真近點角f＞π；短程到達是指地月飛行時間小于地月轉移地心軌道的半個周期，即到達月球時，真近點角f≤π。圖4給出了某一算例中以不同方式到達月球的地月轉移速度增量與飛行時間的關系。圖中下方曲線表示短程到達，上方曲線表示長程到達［16］。

從圖中可以看出，長程到達時，飛行時間隨著轉移速度增量的增加而增加，且轉移時間都在5天以上。因此對于長程到達來說，無論從時間還是能量上都不是最省的，并不適合于載人登月任務。

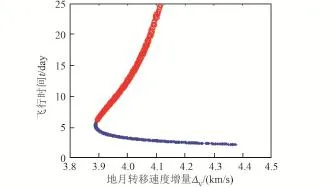
圖4 長程到達和短程到達速度增量與飛行時間的關系［16］Fig.4 The relationship between transfer Δv and transfer time in differen tarriving modes［16］

采用霍曼轉移方式實現奔月任務，往往過程比較簡單，對工程實施的要求相對較低，飛行時間較短，因此這類軌道也是國內外載人登月任務研究中被主要采用的轉移軌道類型。

3.2 利用地?月L1點的轉移方式

從近地停泊軌道上經變軌飛往月球的過渡，根據限制性三體問題的結論，只要過渡軌道初始速度使相應的Jacobi常數C≤C1（稍小于），此時原包圍地球P1和P2月球的兩個零速度面相接并從平動點L1處稍稍打開了一個“狹窄走廊”，如圖5所示，登月飛行器就有可能在越過通道后實現地月轉移。但這只是飛行器可以越過該通道后奔月的一個必要條件，并非充分條件，還要看轉移軌道的起始狀態［24］。

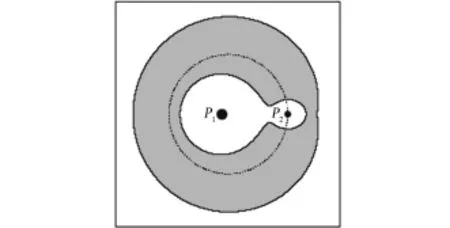
圖5 Jacobi常數C≤C1時對應的飛行器運動可能區域［24］Fig.5 Accessible regions of the spacecraft C≤C1［24］

逆向積分L1點的穩定流形，如果該流形能與近地停泊軌道相交，則理論上在相交處變軌一次即可將飛行器由近地停泊軌道送入到穩定流形（實際是穩定流形所包裹的轉移軌道），從而自動演化到月球引力范圍內。但遺憾的是，當能量C在C1附近時，L1點的穩定流形不能到達距離地球很近的地方，它與地球的最近距離約為0.1個地月平均距離，因此對較低高度的近地停泊軌道而言，一次變軌將飛行器從近地停泊軌道送入到穩定流形是不可能的，需要一段過渡軌道連接，如圖6所示。圖中，PQ為連接弧段，P點在近地停泊軌道上，Q點在L1點的穩定流形上。變動穩定流形的能量以及P、Q點的具體位置，可以找到一條比較節省能量的轉移軌道。由于在平動點L1處的能量開口很小，飛行器進入月球引力范圍之后往往會自動被月球俘獲。

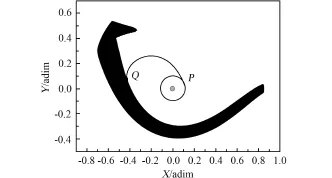
圖6 連接弧段示意圖Fig.6 Schematic diagram of the transition trajectory

通過以上分析可知，如果僅要求登月飛行器實現地月轉移，而對目標環月軌道沒有要求，則通過不變流形的轉移方式比霍曼轉移方式節省能量。但對于載人登月任務而言，環月軌道往往根據月面著陸區預先設計好，因此采用此類型地月轉移軌道，必須施加額外的速度增量使得飛行器到達預定的環月軌道，即整個地月轉移過程一般至少要通過施加三次脈沖完成，前兩次分別在P點和Q點，第三次在近月點附近。正是由于要施加額外的速度增量來完成“搭橋”，所以此類軌道對于實施載人登月任務來說，能量往往并不節省。

圖7給出了一條從高度為200 km的近地停泊圓軌道經兩次變軌進入可轉移軌道最終被月球俘獲的軌道，下圖是上圖經過L1點后的放大（維持時間為1年）。

計算得到連接弧段PQ持續3.33天，從Q點開始到經過L1點耗時362.85天。如果要求進入的環月軌道高度為100 km，則整個轉移過程需要施加的速度增量為 Δv＝3102.11m/s+ 393.93 m/s+658.85 m/s＝4154.89 m/s，該值比霍曼轉移方式還要高，并且達到最優能耗需要耗費相當長的時間，因此從工程實施來看，發射飛行器時通過L1點的不變流形轉移方式并不可取，因為這種轉移軌道既耗時間又耗能量。

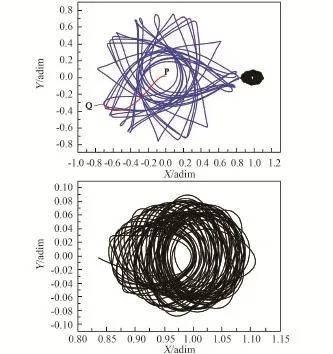
圖7 一條通過L1點被月球俘獲的轉移軌道Fig.7 One transfer trajectory to be captured by the moon through L1 point

3.3 弱穩定邊界轉移方式

弱穩定邊界轉移軌道需要用到日?地系不變流形與地－月系不變流形相交的特性來實現地月轉移。首先，飛行器可以先經由日－地系L1點或L2點的穩定和不穩定不變流形運行到地－月系的L2點之外，然后再經由地－月系的L2點穩定不變流形進入月球引力范圍而被月球俘獲［25］，圖8給出了兩個限制性系統的不變流形相交示意圖［24］。由于日－地系的穩定不變流形可以到達距地球很近的地方，因此可以直接從近地停泊軌道上一次變軌即將飛行器送入到日－地系的穩定不變流形，之后飛行器將經由日－地系的不穩定不變流形進入到地－月系的穩定不變流形而被月球俘獲。如果對環月目標軌道有要求，則需要在目標軌道入軌點處再次變軌，整個過程只需要兩次變軌。這類軌道最先由Belbruno等［26］給出，后來Koon等［27］利用不變流形解釋了這類軌道的動力學機制。這類軌道通常稱為月球彈道轉移軌道（Lunar Ballistic Trajectories）或者弱穩定邊界WSB（Weak Stability Boundary）轉移軌道。

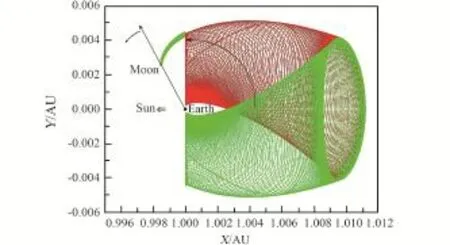
圖8 日?地系的L2點附近的流形與地?月系L2點附近的流形的相交情形［24］Fig.8 Intersections between the invariant manifolds of thesun?earth L2 point and of the earth?moon L2 point［24］

Koon等設計WSB軌道的方法如下：首先計算兩個限制性三體系統對應的不變流形的Poincaré截面，并研究它們的相交情形，從中選出一條拼接軌道，即一部分在日－地系對應的圓型限制性三體系統中，另一部分在地－月系對應的圓型限制性三體系統中，在連接處將這兩者幾何上拼接起來，然后在完整力模型下數值改進以得到實際的轉移軌道［28］。通過初步估算可知，這種類型的轉移軌道所需要的最小能量為3787 m/s，但這里忽略了飛行器由日－地系中能量為C′2的狀態變為地－月系中能量為C2的狀態所需的能量，因為在該處所需的能量隨飛行器的位置不同而不同，所以真正的WSB軌道需要消耗的能量要略大于最優值3787 m/s。

圖9給出了設計的一條WSB轉移軌道在地心慣性系中的圖像，閉合曲線為月球軌道。該轉移軌道耗時102.04天，第一次變軌為3200.07 m/s，第二次變軌為647.63 m/s，總能耗為3847.70 m/s，近地停泊軌道高度為200 km，環月目標軌道高度為200 km。

雖然WSB轉移軌道比傳統的霍曼轉移軌道要節省能量，但這樣的轉移軌道耗時過長，因此，這種類型的轉移軌道也僅僅適用于對時間要求不高的月球探測任務［29］。

3.4 小推力轉移方式

小推力轉移是指采用推力較小的連續推力發動機，通過持續開機將登月飛行器送入月球軌道。該模式可以全程采用小推力轉移，或者可與脈沖式推力結合實現轉移，由于推力較小，其轉移軌道呈現螺旋狀［30?31］，如圖10所示。

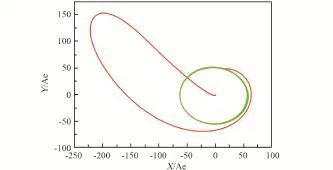
圖9 地心慣性系中的WSB轉移軌道Fig.9 WSB transfer trajectory in the earth inertial coordinate

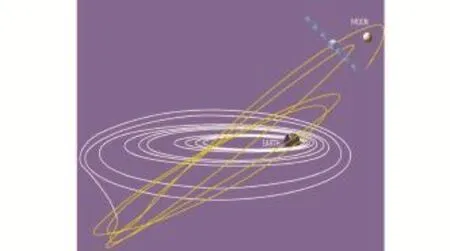
圖10 小推力轉移軌道示意圖Fig.10 Schematic diagram of the low thrust transfertrajectory

利用該方式轉移，飛行器在奔月過程中受到推力較小，一般需要耗費較長的時間，但小推力發動機一般采用新型的推進模式（如電推進），往往具有較高的比沖，因此會減輕飛行器燃料質量，但長的轉移時間會導致航天員更多的消耗，倘若用在載人登月任務中，其實并不能對減輕登月飛行器的質量有太大幫助，往往安全性還更差，因此一般也不采用。

針對以上各種地月轉移軌道類型，表1通過仿真計算進一步對能量消耗和飛行時間做出了比較。

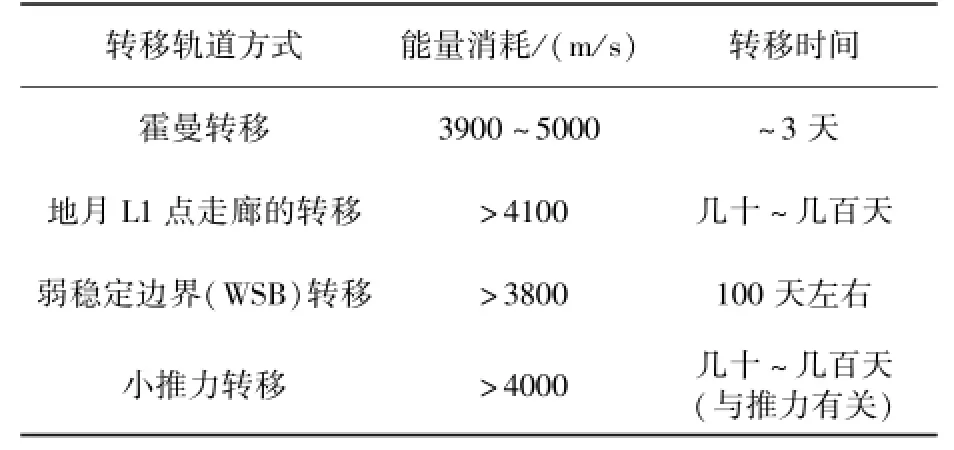
表1 不同地月轉移方式的比較Table 1 Comparision of different lunar transfer modes

綜上，載人登月任務的奔月軌道采用大推力霍曼轉移方式為宜，且應采用短程到達的方式。

4 載人登月地月轉移軌道選擇

通過上述分析可知，對于載人登月任務來說，由于受飛行時間、安全性、可靠性等約束，一般都采用大推力霍曼轉移的地月轉移軌道，對于該類軌道同樣有不同方案，主要包括一般轉移軌道方案、自由返回軌道方案和基于自由返回軌道的變軌方案等。

4.1 一般轉移軌道

一般轉移軌道最為簡單，軌道設計只需要滿足飛行時間、月面著陸區、測控等任務最基本的約束條件即可。

由于設計約束相對較少，此類軌道設計空間往往較大，其飛行時間約在2～5天左右，地月轉移的能量消耗3.9～4.5 km/s，且基本可以到達任意環月軌道，覆蓋不同月面著陸區，在實際任務中可根據工程約束選擇最優的飛行軌道。但采用一般轉移軌道，倘若飛行器在地月轉移過程中發生故障，在不進行軌道機動的前提下，將無法返回地球，因此其安全性相對較低。鑒于這一原因，一般轉移軌道往往被用于無人飛行器轉移（如載人登月任務中的物資轉移），或者是在經歷多次飛行、任務非常成熟時的載人飛行器地月轉移。

4.2 自由返回軌道

自由返回軌道是指登月飛行器在不進行環月制動時，可以不需要軌道機動或只需要很小的推力進行軌道修正就能返回地球的地月轉移軌道，如圖11所示。它是在地月轉移過程中推力系統失效情況下飛行器所能安全返回地球的最省能量軌道，因此具有很高的安全特性［21］。

圖11 自由返回軌道示意圖［21］Fig.11 Schematic diagram of the free return trajectory［21］

根據飛行路徑，自由返回軌道可以分為四類［32］：地心順行繞月自由返回軌道、地心逆行繞月自由返回軌道、地心順行非繞月自由返回軌道和地心逆行非繞月自由返回軌道。地心順行軌道是指飛行器從地球停泊軌道出發時的速度方向與地球自轉方向一致，逆行軌道則表示相反；繞月軌道是指地月轉移軌道的近月點在月球背面，即飛行器繞過月球背面后返回地球，非繞月軌道則是指近月點在月球正面，即飛行器從月球正面利用月球引力轉向后返回地球。非繞月自由返回軌道類似于3.1節提到的長程到達，飛行時間和能量消耗都會大于繞月自由返回軌道，因此并不適合于載人登月任務。另外，對于地心逆行軌道來說，由于其出發速度方向與地球自轉速度方向相反，火箭在將飛行器送入預定軌道時所需要消耗的燃料更多，即運載能力損失更大，因此也一般不用于載人登月任務。在實際工程中一般只選用地心順行繞月自由返回軌道作為載人登月任務的地月轉移軌道。

自由返回軌道所需的最小速度增量一般要大于非自由返回軌道，其所能達到的環月軌道均為逆行軌道，傾角只能集中在相對白道160°～180°之間，且要求的近月距越小，所能到達的環月軌道與白道的夾角越小；進一步轉化到月固系下，其所對應的月面著陸點緯度也只能在約±20°之間（這一值會隨出發時刻的不同稍有變動，最大不超過±25°），如圖12所示［16］。因此地月轉移任務如果采用自由返回軌道，則不能實現全月面到達，只能到達低緯度區域。這與“阿波羅”任務時期所得到的結論相同，“阿波羅”前期任務都采用了自由返回軌道，因此其月面著陸點都選擇在赤道附近［33］。

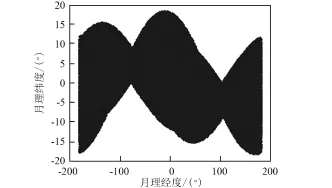
圖12 自由返回軌道所到達的月面著陸區范圍［16］Fig.12 Range of the lunar landing site［16］

4.3 基于自由返回軌道的中途變軌方案

自由返回軌道+中途變軌，亦稱混合軌道，它是指飛行器沿自由返回軌道飛行一定時間后，確保飛行器不出現故障時，通過施加一次中途變軌，使其進入目標軌道，如圖13所示［20］。

混合軌道可以使飛行器的月球軌道到達范圍大大增加，幾乎可達到任意軌道傾角和環月軌道高度（其中升交點不能任意取值，需與軌道傾角相對應）［21］，但對于到達不同的環月軌道，其能量消耗代價不同，圖14給出了到達不同環月軌道傾角，中途變軌所需的速度增量。圖15進一步給出了變軌至環月極軌時，地月轉移出發后不同時刻實施變軌所需的速度增量［21］。

圖13 混合軌道示意圖［21］Fig.13 Schematic diagram of the hybrid trajectory［21］

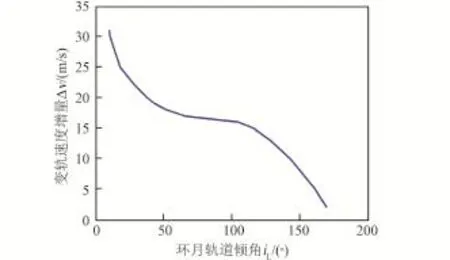
圖14 環月軌道傾角對中途變軌速度增量的影響Fig.14 Influence of the lunar orbit inclination angel on the midway orbit maneuver Δv

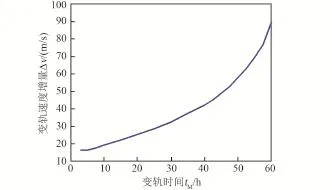
圖15 變軌時刻對變軌速度增量的影響Fig.15 Influence of the orbit maneuver time on the orbit maneuver Δv

從圖中可以看出，采用該方案，改變的軌道面傾角越大，所需要的速度增量越大；當到達同一目標環月軌道時，中途變軌時刻越早，所需的能量越小。

總的來說，該方案只需要較小的變軌速度增量（一般不大于100 m/s），就可實現月面不同緯度區域的探測，但當進行了中途軌道機動之后，地月轉移軌道的自由返回特性就會被破壞，此時倘若飛行器出現故障，則必須要施加額外的速度增量才能使其返回地球，因此其安全性比自由返回軌道有所降低。

4.4 基于自由返回軌道的終端變軌方案

自由返回軌道+終端變軌是指飛行器首先沿自由返回軌道實現地月轉移，到達月球附近后再通過軌道機動實現軌道面的改變，以進入目標環月軌道。在到達月球后，實現飛行器軌道面機動方式有很多種，但為節省能量，一般先將飛行器制動進入一個繞月大橢圓過渡軌道，然后在遠月點通過施加脈沖實現軌道面的改變，因此采用這種變軌方案，環月制動往往需要施加3次速度增量，第一、三次脈沖主要用于改變軌道長半軸，第二次脈沖主要用于軌道面改變，其飛行過程如圖16所示［18］。

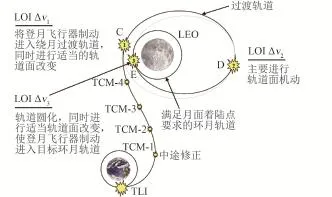
圖16 自由返回軌道+終端變軌飛行示意圖［18］Fig.16 Schematic diagram of the terminal orbit ma?neuver flight based on free return trajecto?ry［18］

該方案同樣可以使飛行器達到任意環月軌道傾角，但變軌至不同環月軌道傾角時，其能量消耗代價相差較大，圖17給出了到達不同環月軌道傾角，終端變軌所需的速度增量。圖18進一步給出了變軌至環月極軌時，完成終端三脈沖變軌所消耗時間對變軌速度增量的影響［21］。

從圖中可以看出，采用該方案，同樣改變的軌道面傾角越大，所需要的速度增量越大；當到達同一目標環月軌道時，三脈沖變軌飛行時間越長（即過渡橢圓軌道半長軸越長），所需的能量越小。

自由返回軌道+終端變軌這一方案是在飛行器到達近月點后才實施軌道機動，在奔月過程中出現任何故障都可以實現無動力返回，因此其安全性相對較高，但這種變軌方案所消耗能量受軌道面差異的影響很大，倘若軌道面變化很大，則其需要的能量較大（遠大于中途變軌方案）；另外由于利用了大橢圓過渡軌道實現軌道面機動，其飛行時間會大大延長，如利用100×9000 km的繞月過渡軌道實現軌道面機動，則飛行時間要比標準飛行時間增加約7小時。

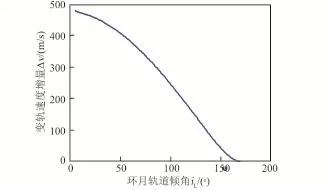
圖17 環月軌道傾角對終端變軌速度增量的影響Fig.17 Influence of the lunar orbit inclination angel on the terminal orbit maneuver Δv

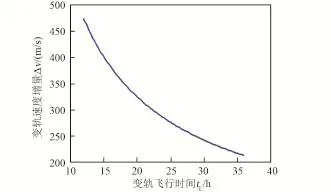
圖18 三脈沖變軌時間對變軌速度增量的影響［21］Fig.18 Influence of the orbit maneuver time on the terminal orbit maneuver Δv［21］

5 結論

本文對地月轉移軌道的類型、求解模型及軌道特性進行了詳細分析，通過分析可知，目前對于載人登月任務而言，最佳的軌道類型仍為大推力霍曼轉移方式，該類型軌道中不同的轉移軌道方案的對比如表2所示。其中自由返回軌道及基于自由返回軌道的終端變軌方案安全性較高，適用于早期的載人登月任務；基于自由返回軌道的中途變軌方案可在任務取得一定成熟經驗后采用；一般轉移軌道可用于貨物運輸或任務非常成熟時的載人飛行。工程中實際采用哪類軌道方案，還需要結合整個系統的安全可靠性及飛行器的能力等進行綜合權衡。

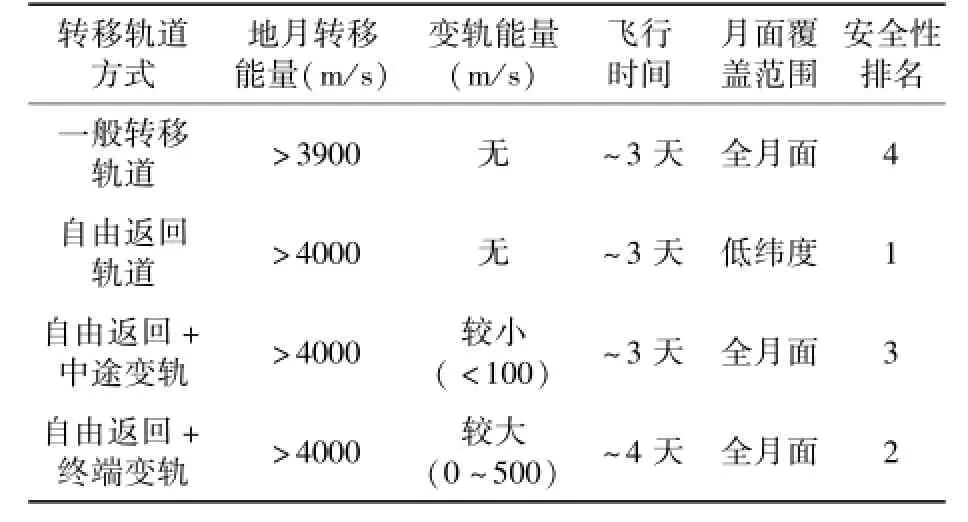
表2 不同地月轉移軌道方案的比較Table 2 Comparision of different lunar transfer trajec?tory schemes

（

）

［1］Penzo P.An analysis of free?flight circumlunar trajectories［C］//AIAA Astrodynamics Conference，New Haven，Con?necticut，1963.

［2］Dallas SS.Moon?to?Earth trajectories［C］//AIAA Astrody?namics Conference，New Haven，Connecticut，1963.

［3］Gibson T.Application of the matched conic model in the stud?y of circumlunar trajectories［R］.NASA 70?35798，1963.

［4］Miele A.Theorem of image trajectories in the Earth?Moons?pace［J］.Acta Astronautica，1960，6（51）：225?232.

［5］Schwaniger A J.Trajectories in the Earth?Moon space with?symmetrical free return properties［R］.NASA Technical Not?eD?1883，Washington DC，1963.

［6］Jesick M，Ocampo C.Automated generation of symmetric lu?nar free?return trajectories［J］.Journal of Guidance，Control and Dynamics，2011，34（1）：98?106.

［7］Baoyin H，McInnes C.Trajectories to and from the lagrange?points and the primary body surfaces［J］.Journal of Guid?ance，Control αnd Dynamics，2006，29（4）：998?1003.

［8］Kluever C A，Pierson B L.Optimal Earth?Moon trajecto?riesusing nuclear electric propulsion［J］.Journal of Guid?ance，Control and Dynamics，1997，20（2）：239?245.

［9］黃誠，胡小工，李鑫.滿足一定約束條件的登月飛行軌道設計［J］.天文學報，2001，42（2）：161?172.Huang Cheng，Hu Xiaogong，Li Xin.Lunar?landing trajectory designing under certain constraints［J］.Acta Astronomica Sinica，2001，42（2）：161?172.（in Chinese）

［10］郗曉寧，曾國強，任萱，等.月球探測器軌道設計［M］.北京：國防工業出版社，2001：51?129.Xi Xiaoning，Zeng Guoqiang，Ren Xuan，et al.Orbit Design of Lunar Probe［M］.Beijing：National Defense Industry Press，2001：51?129.（in Chinese）

［11］曾國強，任萱，郗曉寧.快速設計月球衛星轉移軌道的一種代數方法［J］.國防科技大學學報，2000，22（2）：1?6.Zeng Guoqiang，Ren Xuan，Xi Xiaoning.An algebraic meth?od for fast design of lunar satellite transfer trajectory［J］.Journal of National University of Defense Technology，2000，22（2）：1?6.（in Chinese）

［12］劉林，王歆.月球探測器軌道力學［M］.北京：國防工業出版社，2006：15?50.Liu Lin，Wang Xin.An Orbital Dynamics of Lunar Probe［M］.Beijing：National Defense Industry Press，2006：15? 50.（in Chinese）

［13］劉林，侯錫云，王海紅.關于共線平動點的特征及其在深空探測中的應用［J］.天文學進展，2006，24（2）：174?182.Liu Lin，Hou Xiyun，Wang Haihong.On Characteristics of Collinear Libration Points and Their Application in Deep Space Exploration［J］.Progress in Astronomy，2006，24（2）：174?182.（in Chinese）

［14］徐明，徐世杰.小推力航天器的地月低能轉移軌道［J］.航空學報，2008，29（4）：781?787.Xu Ming，Xu Shijie.Low?energy trajectory from Earth to Moon for low?rhrust spacecraft［J］.Acta Aeronautica et Astro?nautica Sinica，2008，29（4）：781?787.（in Chinese）

［15］寶音賀西，李京陽.載人登月軌道研究綜述［J］.力學與實踐，2015：36（6）：665?673.Baoyin Hexi，Li Jingyang.Review of trajectory design for manned lunar mission［J］.Mechanics in Engineering，2015：36（6）：665?673.（in Chinese）

［16］Peng Q B，Shen H X，Li H Y.Free return orbit design and characteristics analysis for manned lunar mission［J］.Sci Chi?na Tech Sci，2011，54（12）：3243?3250.

［17］彭祺擘，李海陽，李楨等.從空間站出發的奔月軌道設計［J］.國防科技大學學報，2009，31（2）：25?30.Peng Qibo，Li Haiyang，Li Zhen，et al.Trans?lunar trajecto?ry design of lunar probe launched from space station［J］.Journal of National University of Defense Technology，2009，31（2）：25?30.（in Chinese）

［18］Condon G L.Lunar orbit insertion targeting and associated outbound mission design for lunar sortie missions［R］.Flt?Dyn?CEV?06?72，2007.

［19］彭祺擘，李楨，李海陽.載人登月飛行方案研究［J］.上海航天，2012（5）：14?19.Peng Qibo，Li Haiyang，Li Zhen.Analysis on manned lunar mission flight mode［J］.Aerospace Shanghai，2012（5）：14?19.（in Chinese）

［20］黃文德，郗曉寧，王威.基于雙二體假設的載人登月混合軌道特性分析及設計［J］.國防科技大學學報，2010，32（4）：61?67.Huang Wende，Xi Xiaoning，Wang Wei.Characteristics anal?ysis and desing of hybrid trajectory for manned lunar landing mission based on double two?body model［J］.Journal of Na?tional University of Defense Technology，2010，32（4）：61?67.（in Chinese）

［21］彭祺擘.考慮應急返回能力的載人登月軌道優化設計及特性分析［D］.長沙：國防科技大學，2012.Peng Qibo.Optimal Trajectory Design and Characteristics A?nalysis for Manned Lunar Landing Mission with Emergency Return Capability［D］.Changsha：National University of De?fense Technology，2012.（in Chinese）

［22］戚發軔，朱仁璋，李頤黎.載人航天器技術［M］.北京：國防工業出版社，2003：42?44.Qi Faren，Zhu Renzhang，Li Yili.Manned Spacecraft Tech?nology［M］.Beijing：National Defense Industry Press，2001：42?44.（in Chinese）

［23］劉林，劉慧根.地月系中探測器定點在三角平動點附近的位置漂移及其控制問題［J］.宇航學報，2008，29（4）：1222?1227.Liu Lin，Liu Huigen.Orbit drift and control of the spacecraft around the triangular libration points in the Earth?Moon system［J］.Journal of Astronautics，2008，29（4）：1222?1227.（in Chinese）［24］侯錫云，劉林.共線平動點的動力學特征及其在深空探測中的應用［J］.宇航學報，2008，29（3）：736?747.Hou Xiyun，Liu Lin.The dynamics and applications of the collinear libration points in deep space exploration［J］.Jour?nal of Astronautics，2008，29（3）：736?747.（in Chinese）

［25］龔勝平，李俊峰，寶音賀西等.基于不變流形的登月軌道設計［J］.應用數學和力學，2007，28（2）：183?190.Gong Shengping，Li Junfeng，Baoyin Hexi，et al.Lunar landing trajectory design based on invariant manifold［J］.Ap?plied Mathematics and Mechanics，2007，28（2）：183?190.（in Chinese）

［26］Belbruno E A.Lunar capture orbits，a method of constructing earth moon trajectories and the lunar gas mission［C］//19th AIAA/PGLR/JSASS International Electric Propulsion Confer?ence，Colorado Springs，Colorado，May，1987.AIAA?87?1054.

［27］Koon W S，Lo M W，Marsden J E，etal.Low energy transfer to the moon［J］.Celestial Mechanics and Dynamical Astrono?my，2001，81（1）：63?73.

［28］徐明.平動點軌道的動力學與控制研究綜述［J］.宇航學報，2009，30（4）：1299?1313.Xu Ming.Overview of orbit dynamics and control for libration point orbits［J］.Journal of Astronautics，2009，30（4）：1299?1313.（in Chinese）

［29］何巍，徐世杰.地月低能轉移軌道設計方法研究［J］.宇航學報，2006，27（5）：965?969.He Wei，Xu Shijie.Research on low energy trajectory design method between Earth and Moon［J］.Journal of Astronautic，2006，27（5）：965?969.（in Chinese）

［30］王劼，崔乃剛，劉暾.定常幅值小推力登月飛行器軌道研究［J］.航空學報，2001，22（1）：6?9.Wang Jie，Cui Naigang，Liu Dun.On constant?amplitude low?thrust lunar probe trajectories［J］.Acta Aeronautica et Astronautica Sinica，2001，22（1）：6?9.（in Chinese）

［31］王劼，崔乃剛，劉暾.小推力登月飛行器軌道初步研究［J］.飛行力學，2000，18（2）：46?49.Wang Jie，Cui Naigang，Liu Dun.Preliminary study on mini?mum?fuel lunar probe trajectories［J］.Flight Dynamics，2000，18（2）：46?49.（in Chinese）

［32］白玉鑄.載人登月軌道設計相關問題研究［D］.長沙：國防科技大學，2010.Bai Yuzhu.Research on Trajectory Design for Manned Lunar Landing Mission［D］.Changsha：National University of De?fense Technology，2010.（in Chinese）

［33］Head J W.Scientific rationale summaries for Apollo candidate lunar exploration landing sites［R］.NASA?CR?109867，1970.

Review of Lunar Transfer Trajectory Modes for Manned Lunar Mission

PENG Qibo，ZHANG Hailian
（Manned Space System Research Center，Beijing 100094，China）

Based on the status and research progress of the earth?lunar transfer trajectory in China and abroad，the design model and constraints of the earth?lunar transfer trajectory were studied and the characteristic and adaption of different types of trajectories were analyzed in this paper.Accord?ing to the features of human lunar exploration mission，the types of the lunar transfer trajectory and the design schemes were discussed.Simulation was conducted to compare the available trajectory re?search results，then the flight duration，energy consumption and lunar landing destination for differ?ent types of trajectories were analyzed.Finally，suggestions on human lunar exploration mission's trajectory design were proposed which may serve as a reference for the further study.

mannedlunar mission；earth?lunar transfer trajectory；design constraints；earth?lunarli?bration point；free return trajectory

V412.4

A

1674?5825（2016）06?0663?10

2016?05?31；

2016?09?11

彭祺擘（1982－），男，博士，助理研究員，研究方向為載人登月總體任務分析與設計。E?mail：poochie003＠163.com