基于不變流形的地月L2點Halo軌道轉移軌道設計

彭 坤，李明濤，王 平，田 林，果琳麗，楊 雷

（1.中國空間技術研究院載人航天總體部，北京100094；2.中國科學院空間科學與應用研究中心，北京100190）

基于不變流形的地月L2點Halo軌道轉移軌道設計

彭 坤1，李明濤2，王 平1，田 林1，果琳麗1，楊 雷1

（1.中國空間技術研究院載人航天總體部，北京100094；2.中國科學院空間科學與應用研究中心，北京100190）

針對Halo軌道轉移軌道設計不易收斂的問題，結合月球探測背景，分析了地月L2點Halo軌道及其不變流形可靠近月球的運動軌跡特性，給出基于二分法的先粗選后精選的零消耗轉移軌道搜索方法并研究得出Halo軌道全相位點入軌的零消耗轉移軌道不超過2條，提出一種最小x軸約束的近月點終止條件和自適應退步搜索的改進微分修正算法，對Halo軌道全相位點入軌的轉移軌道設計進行求解。仿真結果表明，該改進微分修正算法收斂速度快，能有效避免奇異，且適應性強，能搜索出全相位點入軌的所有轉移軌道。

月球探測；平動點；Halo軌道；不變流形；轉移軌道

1 引言

近年來，隨著月球探測熱潮的興起，地月系統L2點（簡稱EML2點）附近的Halo軌道逐漸受到航天界的重視。早在阿波羅任務時期，Farquhar就提出在EML2點附近Halo軌道放置一顆衛星，為阿波羅月球背面探測任務提供測控通信支持［1］，由于資金原因最終計劃取消，但該方案為月球背面探測任務的測控通信方案提供了一種思路；也有學者提出可以將登月航天器停泊在EML2點附近Halo軌道，航天員在航天器上遙控著陸月面的機器人進行探測［2］。對于后者，往往需要兩個航天器在Halo軌道進行交會，因此需研究月球到Halo軌道全相位位置的轉移軌道特性。

在平動點Halo軌道轉移軌道研究方面，How?ell等利用不變流形和微分修正算法求解了最佳Halo軌道入軌點的日地系統L1點Halo軌道與地球之間的轉移軌道［3］。Zazzera等［4］人基于不變流形和龐加萊截面設計了無約束轉移軌道。胡少春等［5］將序優化理論與微分修正相結合求解日地系統L1點Halo軌道到地球的轉移軌道，增加了微分修正的收斂范圍。李明濤［6?8］系統研究了日地系統和地月系統平動點Halo軌道轉移軌道設計，推導了各軌道約束的微分修正公式，求解了多約束條件下的精確轉移軌道。喬棟等［9］以嫦娥二號擴展任務為背景設計了環月軌道到日地L2點的轉移軌道。張景瑞和曾豪［10?11］在李明濤的基礎上，設計了求解日地系統Halo軌道的多約束轉移軌道分層搜索算法以及不同月球借力條件的地月系統Halo軌道轉移軌道設計。

雖然上述文獻對平動點Halo軌道轉移軌道搜索算法進行了多方面研究，但對于Halo軌道到次天體的轉移軌道搜索算法并未進行詳細討論，且大多研究為Halo軌道上單個入軌點的轉移軌道，并非針對Halo軌道全相位點進行的轉移軌道設計。本文在圓型限制性三體模型下，以月球到地月系統L2點Halo軌道的轉移軌道設計為例，提出一種基于不變流形的終止條件快速識別和自適應退步搜索的平動點轉移軌道改進微分修正算法，減少轉移軌道搜索迭代次數和軌道仿真時間，同時提高轉移軌道收斂性，并分析了月球到Halo軌道不同相位的轉移軌道特性，為未來實施基于平動點的月球探測計劃提供參考。

2 EML2點Halo軌道及其不變流形設計分析

2.1 圓型限制性三體模型

對Halo軌道轉移軌道的軌道特性初步分析時，無需采用復雜的高精度星歷模型［2］，本文采用圓型限制性三體模型來設計Halo軌道及其轉移軌道。令地球m1和月球m2為主天體，假設m1和m2繞其地月系統質心做角速度為ω的勻速圓周運動，且航天器質量m3?m2＜m1。以地月系統質心為原點，地月連線由地球指向月球方向為x軸，z軸沿角動量方向，建立會合坐標系O－xyz。利用拉格朗日方程可推導出會合坐標系下航天器的動力學方程，并進行歸一化處理可得式（1）［12］：

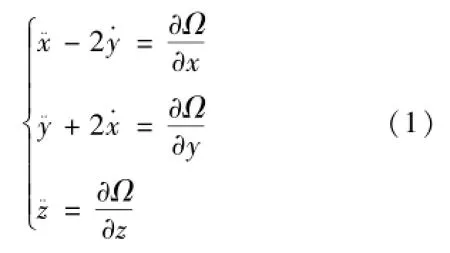
式中變量定義如式（2）：

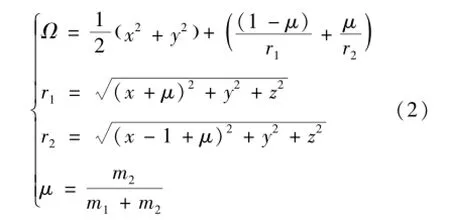
2.2 Halo軌道設計與分析

將動力學方程從會合坐標系下轉化到平動點L2坐標系下，并除以距離尺度 γ2，即 ρ＝（ξ，η，ζ）T＝1/γ2·（x－x2，y，z）T，則可將其平動點附近運動構造為式（3）形式：

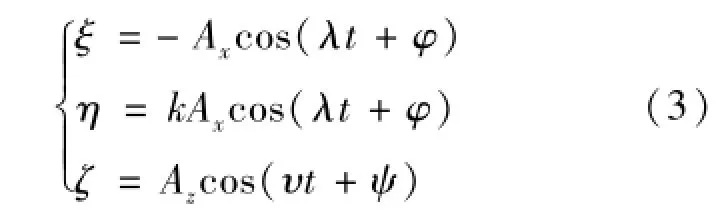
其中Ax和Az分別表示平面內、外的振幅，λ和υ分別表示平面內、外的頻率，φ和ψ為相位角。當λ和υ相等時則形成Halo軌道。采用Richardson三階近似值作為Halo軌道初值［13］。

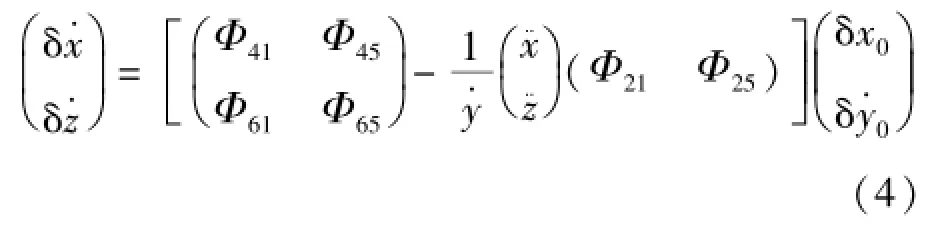
式中Φij為狀態轉移矩陣Φ分量。根據以上方法可求解出EML2點附近的Halo軌道在歸一化單位下的飛行軌跡，如圖1和圖2。圖1為Az＝8000 km的Halo軌道三視圖，圖2為Az＝2000～32000 km的南北向Halo軌道簇。由圖2可知，Halo軌道按照其z軸偏向，可分為南、北向兩簇。

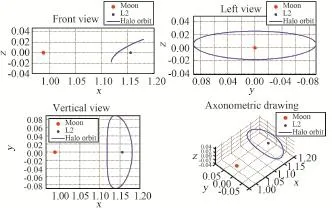
圖1 EML2點單個Halo軌道軌跡Fig.1 Single Halo orbit near EML2 point

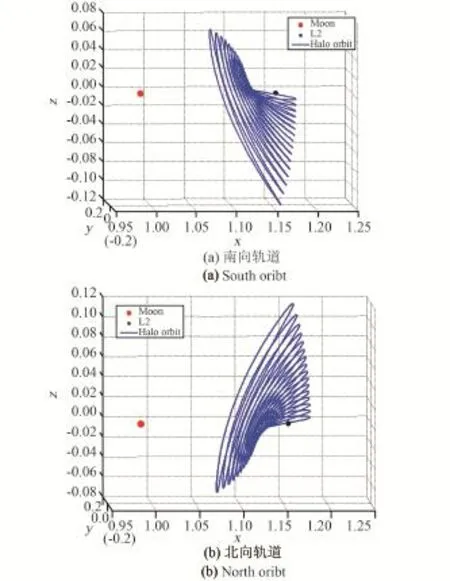
圖2 EML2點南北向Halo軌道簇Fig.2 North and south Halo orbit cluster near EML2 point

2.3 Halo軌道不變流形設計與分析

不變流形是與Halo軌道光滑連接的一簇空間軌道，分為穩定流形和不穩定流形。其中穩定流形逐漸趨近Halo軌道，不穩定流形逐漸遠離Halo軌道［12］。因此，可以將Halo軌道的不變流形作為Halo軌道轉移軌道的初值，在其基礎上進行調整可得到Halo軌道轉移軌道。

不變流形計算過程主要有三步［12］：1）計算Halo軌道某點狀態及其積分一個周期后狀態所對應的狀態轉移矩陣Φ（0，T）（也稱單值矩陣）；2）根據不變流形的類型和方向計算該點Φ（0，T）的特征向量、擾動量，從而求出該點不變流形初始狀態；3）利用動力學方程進行積分，得到不變流形的軌跡。

圖3給出Az＝8000 km的Halo軌道的不穩定流形和穩定流形在歸一化單位下的軌跡，擾動值ε＝50 km，積分時間ΔT＝18 d。由圖3可知，EML2點Halo軌道的左向流形逐漸靠近月球，可以作為轉移軌道到達環月軌道；而其右向流形則延伸到遠離月球的方向，無法作為轉移軌道到達環月軌道。

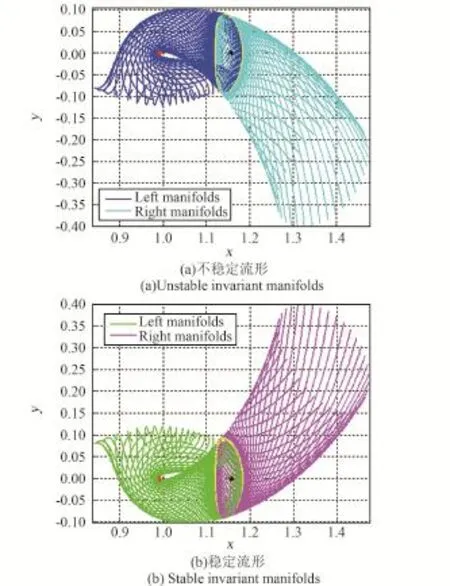
圖3 EML2點Halo軌道的不變流形Fig.3 Invariant manifolds of Halo orbit near EML2 point

3 基于不變流形的零消耗轉移軌道分析

由2.3節指出的不變流形軌跡特性可知，利用左向穩定流形可以設計從環月軌道到L2點Halo軌道的轉移軌道。若不變流形的最小月心距等于環月軌道的月心距，則該不變流形可直接作為轉移軌道，稱為零消耗轉移軌道（入軌點處無需變軌）［8］。以下以Az＝8000 km的Halo軌道為例，設環月軌道高度為HL＝100 km，即近月點月心距為RLP＝1837.400 km，分析其零消耗轉移軌道特點。

1）將Halo軌道按時間等分為360段，初始點為1，與重點361重合，如圖4所示。

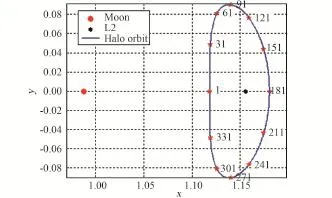
圖4 EML2點Halo軌道分段Fig.4 Different segments of Halo orbit near EML2 point

2）生成Halo軌道上每個節點的左向穩定流形，積分時間取為ΔT＝18 d，如圖5所示。計算每條不變流形距離月球的最小月心距，看是否有流形最小月心距等于環月軌道月心距。由圖5可得，整圈Halo軌道有兩處（約為86節點和186節點）不變流形的最小月心距與環月軌道月心距相等，可以作為零消耗轉移軌道。

3）按照文獻［8］的思路，可采用二分法求解精確的Halo軌道不變流形節點。本文采用先粗選，再精選的流程搜索精確的Halo軌道不變流形節點。首先，選取Halo軌道上一定間隔的采樣點，計算其不變流形最小月心距與環月軌道月心距的差值，記錄月心距差值突變的采樣點數。本文間隔10個節點采樣，既保證采樣精度，同時減少計算量。其次，以差值突變處的前后兩個采樣點作為邊界，設置月心距誤差精度，采用二分法精確搜索滿足月心距約束條件的節點。

4）根據以上算法，可以精確求解出2條滿足月心距約束的零消耗轉移軌道，其結果如圖6～7和表1所示。由搜索結果可知，若利用天然不變流形設計零消耗的轉移軌道，則滿足近月點月心距約束的轉移軌道個數較少，無法滿足Halo軌道全相位（1～361節點）的軌道轉移需求。

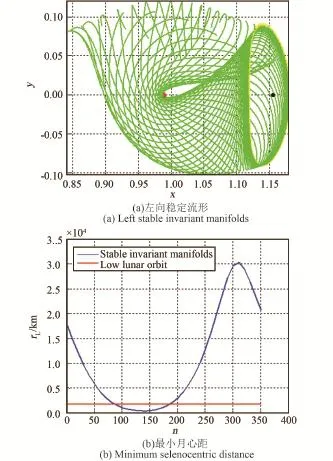
圖5 EML2點Halo軌道左向穩定流形及其最小月心距Fig.5 Left stable invariant manifolds of Halo orbit near EML2 point and its minimum selenocentric dis?tance

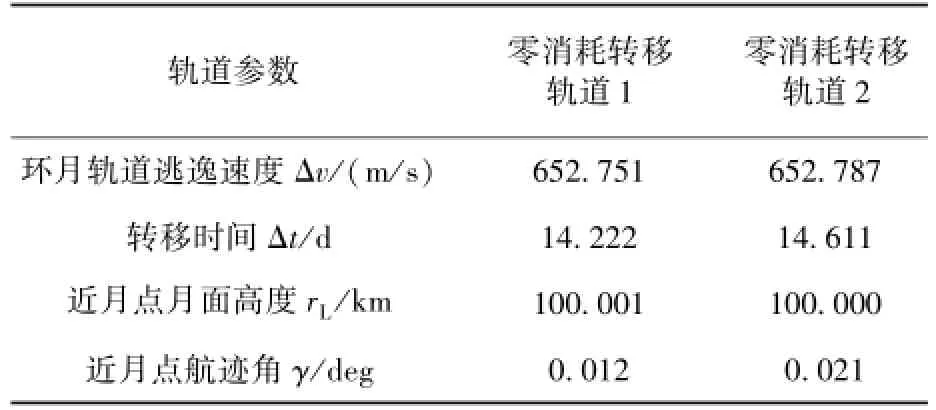
表1 零消耗轉移軌道搜索結果Table 1 Search results of zero consumption transfer trajectory

4 基于不變流形的兩脈沖轉移軌道改進微分修正設計

4.1 問題描述

為滿足Halo軌道上全相位軌道轉移的要求，需要在天然不變流形的基礎上，在Halo軌道入軌點加入脈沖變軌，使穩定流形的近月點月心距滿足約束，此時形成的流形稱為受攝流形［12］。同時在近月點施加脈沖，使航天器從環月軌道進入受攝流形。通過這兩次脈沖變軌，可得到滿足Halo軌道全相位點入軌的轉移軌道［8］。由于Halo軌道處于三體混沌區內，其動力學特性具有強非線性，轉移軌道搜索容易發散，本文考慮以其不變流形為初值，進行微小速度增量調整，得到入軌速度增量較小的兩脈沖轉移軌道。

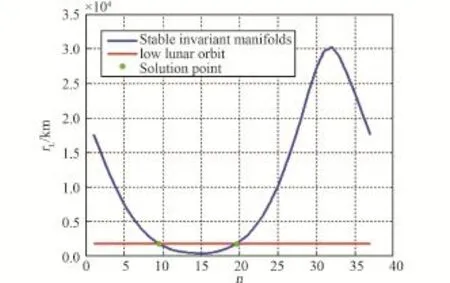
圖6 零消耗轉移軌道精確入軌點Fig.6 Precise injection point of zero consumption transfer trajectory

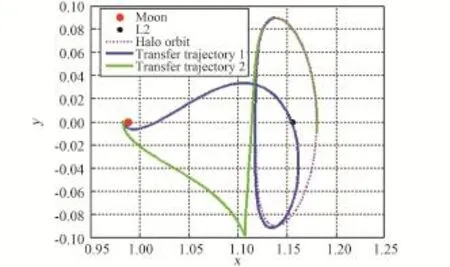
圖7 零消耗轉移軌道軌跡Fig.7 Zero consumption transfer trajectory

4.2 微分修正算法

本文重點研究轉移軌道特性及其設計方法，故主要考慮近月點月心距約束a1＝和航跡角約束 a4＝sinγ－sinγdes，其中RfT＝Rf－RT為相對月球中心的位置矢量，Rf為航天器位置矢量，RT為月球位置矢量，Rdes為月心距目標值，γ為航天器航跡角，γdes＝0°為航跡角目標值。為減少修正約束量，采用航跡角為終止條件，則入軌點速度增量的微分修正算法如式（5）［7］：

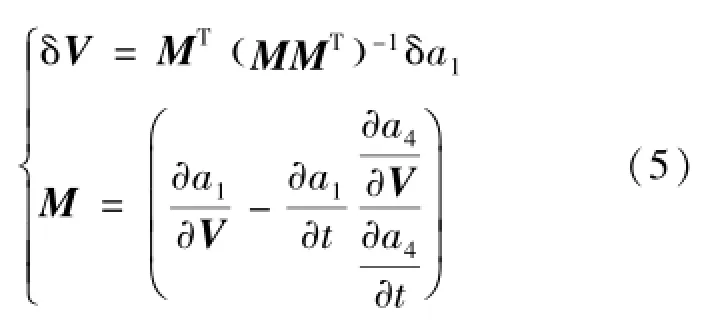
通過求導鏈式法則可得式（6）：

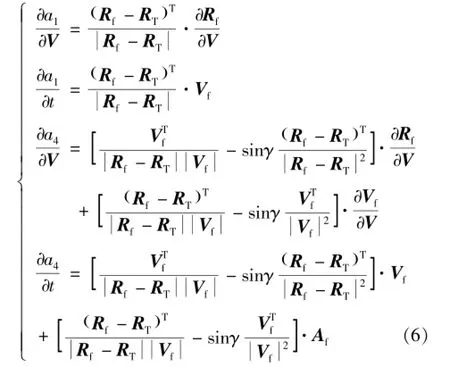
令狀態轉移矩陣為Φ，則可得終端位置速度與初始位置速度的轉換關系，如式（7）所示：

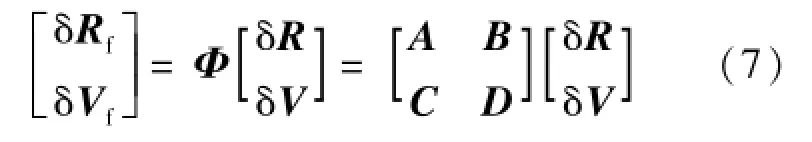
由式（7）可知終端位置速度與初始速度的轉換關系分別對應Φ的一部分，如式（8）：

4.3 快速終止條件設計

在微分修正的軌道積分過程中，需要判斷a4＝sinγ－sinγdes＝0。若直接判斷a4＝0，則有時會收斂到遠月點；同時對于Halo軌道上n＝1或181的節點，其起點位置即滿足a4＝0，會導致奇異。為此，有些學者對航跡角終止條件進行處理，以增加算法收斂性。文獻［11］中設置固定積分時間ΔT，找出所有a4＝0的點，并比較其月心距，以最小月心距作為其積分終止點，該方法大大改善了算法收斂性。但該算法每次需要積分固定時間ΔT，且需要比較月心距，使每次軌道積分時間較長；同時該算法也會將遠月點作為積分終止點，造成修正矩陣不準。

本文考慮近月點的特征，加入航跡角導數，快速確定近月點，節省軌道積分時間；同時加入最小x軸約束，避免n＝1或181節點處產生奇異以及收斂到月心距較大的局部近月點。其終止條件判斷公式如式（9）：

4.4 自適應退步搜索

由于Halo軌道周圍相空間的強非線性，即使以不變流形為初值，在微分修正過程中也會出現終止條件不滿足a4＝0，從而給出錯誤的修正矩陣信息，導致轉移軌道發散或收斂到入軌速度增量較大的轉移軌道上。為此，本文提出一種自適應退步搜索。當采用微分修正算法給出的修正值時，若軌道積分停止到固定時間ΔT且月心距較大，則視為迭代錯誤返回上一步速度增量值，并將修正值減半后再進行積分，如此不斷循環直至迭代跳出錯誤區域。其具體算法如式（10）所示：

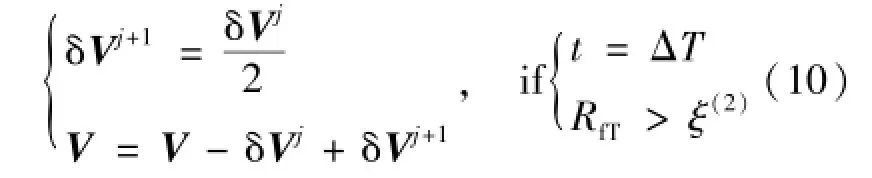
式中，RfT＝‖RfT‖，ξ（2）為L2點距離月球的無量綱化長度。

4.5 設計流程

總結以上策略，可得到兩脈沖轉移軌道設計流程，如圖8所示。

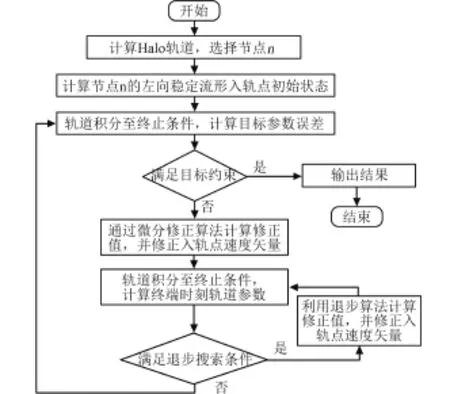
圖8 兩脈沖轉移軌道改進微分修正算法Fig.8 Improved differential correction algorithm for designing two?impulse transfer trajectory

5 兩脈沖轉移軌道仿真驗證

5.1 仿真參數

考慮對月球的覆蓋性要求，Halo軌道設為地月L2點的北向Halo軌道，其z軸幅值Az＝8000 km［2］。設轉移軌道的近月點月面高度100 km，即目標月心距為Rdes＝1837.400 km，目標航跡角為γdes＝0°。由2.3節分析可知，不變流形積分18 d左右就可以到達月球附近，故設轉移軌道最長飛行時間ΔT＝20 d。

5.2 快速終止條件驗證仿真

取Halo軌道上節點n＝1為入軌點，仿真比較本文快速終止條件（終止條件1）與γ＝0°的最小月心距終止條件（終止條件2）的計算速度和結果，如圖9所示。本文快速終止條件一次軌道積分所用仿真時間為t1＝0.79 s，γ＝0°的最小月心距終止條件的仿真時間為t2＝0.98 s，前者每次軌道積分比后者快0.19 s，說明本文終止條件軌道仿真速度更快。

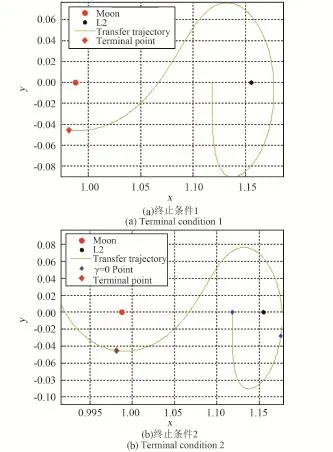
圖9 兩種終止條件的轉移軌道飛行軌跡Fig.9 The transfer trajectories with two terminal conditions

5.3 自適應退步搜索驗證仿真

取Halo軌道上節點n＝136為入軌點，搜索其對應的兩脈沖轉移軌道并驗證自適應退步搜索策略，搜索結果如圖10所示。圖10中深藍色軌跡為正常微分修正迭代軌跡，淺綠色軌跡為退步搜索軌跡，品紅色粗實線軌跡為最終搜索得到的轉移軌道。由圖10可明顯看出，微分修正迭代到第2步時就出現了迭代錯誤的情況，此時積分終止時間為ΔT＝20 d，但其航跡角γ≠0°，該狀態對應的修正矩陣信息是錯誤的（圖中最上面一條軌跡）。通過自適應退步搜索，經過5步退步搜索后（圖中淺綠色軌跡）找到滿足γ＝0°的狀態，再進行微分修正迭代，最后搜索到滿足約束條件的轉移軌道（圖中品紅色軌跡）。

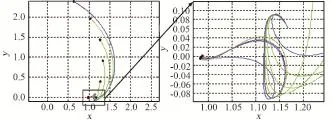
圖10 自適應退步搜索策略的迭代軌跡Fig.10 Iteration trajectories of adaptive backstep?ping search strategy

5.4 全相位入軌點轉移軌道設計仿真

采用改進的微分修正算法，每隔3個節點采樣對全相位Halo軌道入軌點設計轉移軌道，其仿真結果如圖11～13所示。圖11繪制了搜索到的全相位Halo軌道入軌點對應的轉移軌道。由圖11可知，所有的轉移軌道都收斂到兩條軌道附近，這2條軌道對應零消耗轉移軌道。圖12和圖13分別為Halo軌道上不同節點作為入軌點的轉移軌道的轉移時間和入軌點速度增量。由圖12和圖13可知，對于Az＝8000 km的北向Halo軌道，本算法搜索到的以不變流形為基礎的轉移軌道轉移時間范圍為9～19 d；入軌點速度增量范圍為0～8 m/s，屬于小速度增量。

6 結論

1）利用天然不變流形可設計環月軌道到Ha?lo軌道的零消耗轉移軌道，但其入軌點較少，一般最多有2個；

2）本文提出的利用最小x軸約束的近月點終止條件和自適應退步搜索的改進微分修正算法可快速準確地搜索全相位Halo軌道入軌點對應的兩脈沖轉移軌道；

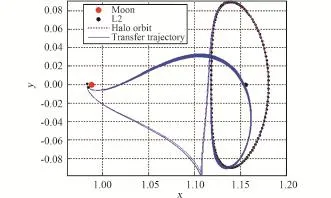
圖11 全相位Halo軌道入軌點對應的轉移軌道Fig.11 Transfer trajectories for all phase injection points of Halo orbit

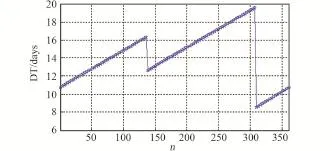
圖12 Halo軌道上不同入軌點轉移軌道的轉移時間Fig.12 Transfer time of transfer trajectories for all phase injection points of Halo orbit

圖13 Halo軌道上不同入軌點轉移軌道的入軌速度增量Fig.13 Velocity increment of transfer trajectories for all phase injection points of Halo orbit

3）Halo軌道上不同相位點對應的基于不變流形的兩脈沖轉移軌道基本收斂到2條零消耗轉移軌道附近，入軌點變軌速度增量較小。

（

）

［1］Farquhar R W.Lunar communications with libration?point satellites［J］.Journal of Spacecraft and Rockets，1967，4（10）：1383?1384.

［2］Hopkins J B，Pratt W，Buxton C，et al.Proposed orbits and trajectories for human missons to the Earth?Moon L2 region［C］//64th International Astronautical Congress，Beijing，China，2013.

［3］Howell K C，Barden B T，Lo M W.Application of dynamical systems theory to trajectory design for a libration point mission［J］.Journal of Astronautical Sciences，1997，45（2）：161?178.

［4］Zazzera F B，Topputo F，Massari M.Assessment of mission design including utlizatlon of libration points and weak stabili?ty boundaries［R］.ESTEC contract No.18147/04/NL/MV，2004

［5］胡少春，孫承啟，劉一武.基于序優化理論的暈軌道轉移軌道設計［J］.宇航學報，2010，31（3）：662?668.Hu S C，Sun C Q，Liu Y W.Transfer trajectory design for Halo orbit based on ordinal optimization theory［J］.Journal of Astronautics，2010，31（3）：662?668.（in Chinese）

［6］Li M T，Zheng J H.The optimization of transfer Irajectory for small amplitude Halo orbits［J］.Measurement and Control，2008，41（3）：81?84.

［7］李明濤，鄭建華，于錫崢，等.約束條件下的Halo軌道轉移軌道設計［J］.宇航學報，2009，30（2）：437?441.Li M T，Zheng J H，Yu X Z，et al.Transfer trajectory design for Halo orbit with multiple constraints［J］.Journal of Astro?nautics，2009，30（2）：437?441.（in Chinese）

［8］李明濤.共線平動點任務節能軌道設計與優化［D］.北京：中國科學院空間科學與應用研究中心，2010.Li M T.Low energy trajectory design and optimization for col?linear libration points missions［D］.Beijing：Center for Space Science and Applied Research，Chinese Academy of Sci?ences，2010.（in Chinese）

［9］Qiao D，Cui P Y，Wang Y M，et al.Design and analysis of an extended mission of CE?2：from lunar orbit to Sun?Earth L2 region［J］.Adv Space Res，2014，54（10）：2087?2093.

［10］張景瑞，曾豪，李明濤.日地Halo軌道的多約束轉移軌道分層微分修正設計［J］.宇航學報，2015，36（10）：1114?1124.Zhang J R，Zeng H，Li M T.Hierarchical differential correc?tion based transfer trajectory design for Halo orbit with multi?ple constraints［J］.Journal of Astronautics，2015，36（10）：1114?1124.（in Chinese）

［11］張景瑞，曾豪，李明濤.不同月球借力約束下的地月Halo軌道轉移軌道設計［J］.宇航學報，2016，37（2）：159?168.Zhang J R，Zeng H，Li M T.A design method for Earth?Moon Halo orbit transfer trajectory under different constraints to Moon gravity?assisted maneuvers［J］.Journal of Astronau?tics，2016，37（2）：159?168.（in Chinese）

［12］李言俊，張科，呂梅柏，等.利用拉格朗日點的深空探測技術［M］.西安：西北工業大學出版社，2015：21?129.Li Y J，Zhang K，Lv M B，et al.Deep Space Exploration Technology by using Lagrange Point［M］.Xi'an：Northwest?ern Polytechnical University Press，2015：21?129.（in Chi?nese）

［13］劉林，侯錫云.深空探測器軌道力學［M］.北京：電子工業出版社，2012：86?157.Liu L，Hou X Y.Orbit Mechanics of Deep Space Probe［M］.Beijing：Publishing House of Electronics Industry，2012：86?157.（in Chinese）

Transfer Trajectory Design for EML2 Halo Orbit Based on Invariant Manifolds

PENG Kun1，LI Mingtao2，WANG Ping1，TIAN Lin1，GUO Linli1，YANG Lei1
（1.Institute of Manned Space System Engineering，China Academy of Space Technology，Beijing 100094，China；2.Technology and Engineering Center for Space Utilization，Chinese Academy of Sciences，Beijing 100190，China）

To cope with the problem that the transfer trajectory design for Halo orbit is difficult to convergence，and considering the background of lunar exploration，the trajectory characteristic of Halo orbit around Earth?Moon L2 point and its invariant manifolds that can reach the moon were ana?lyzed in this paper.Then a hierarchical bisection method to design zero consumption transfer trajec?tory for the Halo orbit was given and the number of zero consumption transfer trajectory for all phase injection points was no more than two.Finally，an improved differential correction method including the perilune terminal condition with minimum x?axis constraint and adaptive backstepping search strategy was proposed to design transfer trajectories for all phase injection points of the Halo orbit.The simulation results indicate that the improved differential correction method has fast convergence speed and can effectively avoid the singularity，moreover it has strong adaptability and can search out transfer trajectories for all phase injection points of the Halo orbit.

lunar exploration；libration point；Halo orbit；invariant manifolds；transfer trajectory

V412.4

A

1674?5825（2016）06?0673?07

2016?06?15；

2016?10?14

載人航天預先研究項目（010701）

彭坤（1984－），男，博士，高級工程師，研究方向為航天器總體與軌道設計。E?mail：bhkpeng＠126.com