多滯量Lotka-Volterra競爭捕食系統的正周期解

任睿超，孫潔

（西北大學現代學院 基礎部，陜西 西安 710130）

多滯量Lotka-Volterra競爭捕食系統的正周期解

任睿超，孫潔

（西北大學現代學院 基礎部，陜西 西安 710130）

運用Mawhin重合度定理和積分不等式構造了有界開集，討論了一類帶任意多時滯的3種群非自治Lotka-Volterra競爭捕食系統，給出了正周期解存在的充分條件，在系數滿足一定的條件時得到了周期振蕩的結論．

Lotka-Volterra競爭系統；正周期解；Mawhin重合度定理

1 引言及預備知識

近年來，在多時滯非線性生物種群模型中，對于具有任意有限個滯量的研究正逐漸成為學者們關注的問題[1-8]．文獻[1]運用重合度定理討論了一類帶有多滯量的Lotka-Volterra3種群互惠系統的正周期解，本文在此基礎上繼續討論3種群非自治Lotka-Volterra競爭捕食系統

的正周期解，其中：x（ t）表示食餌種群密度；y1（ t）和y2（ t）表示2個競爭捕食種群密度；r（ t）為食餌的出生率；r1（ t）為捕食種群1的出生率，且d（ t）為捕食種群2的自然死亡率（假設捕食種群2僅依賴于捕獲食餌

2 主要結果及證明

定理1 若系統（1）滿足條件：

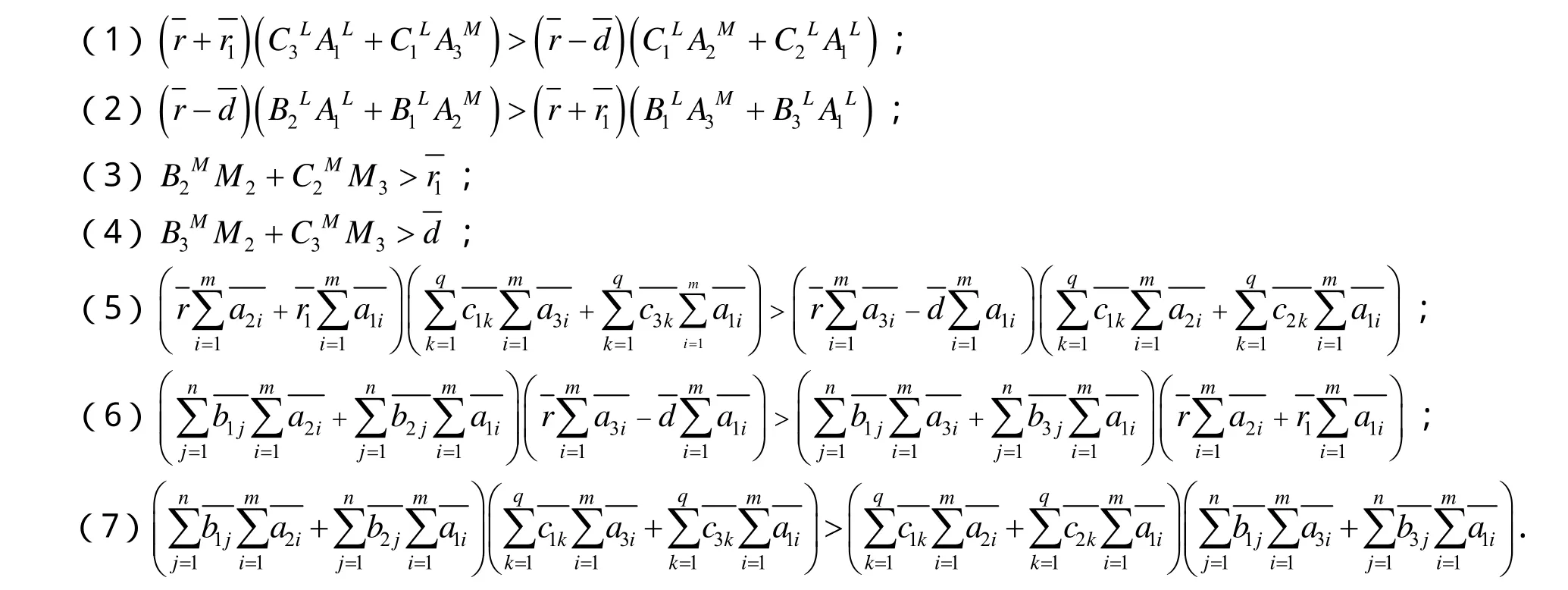
則系統（1）必至少存在一個正ω周期解，其中：

同理，根據比較原理，有

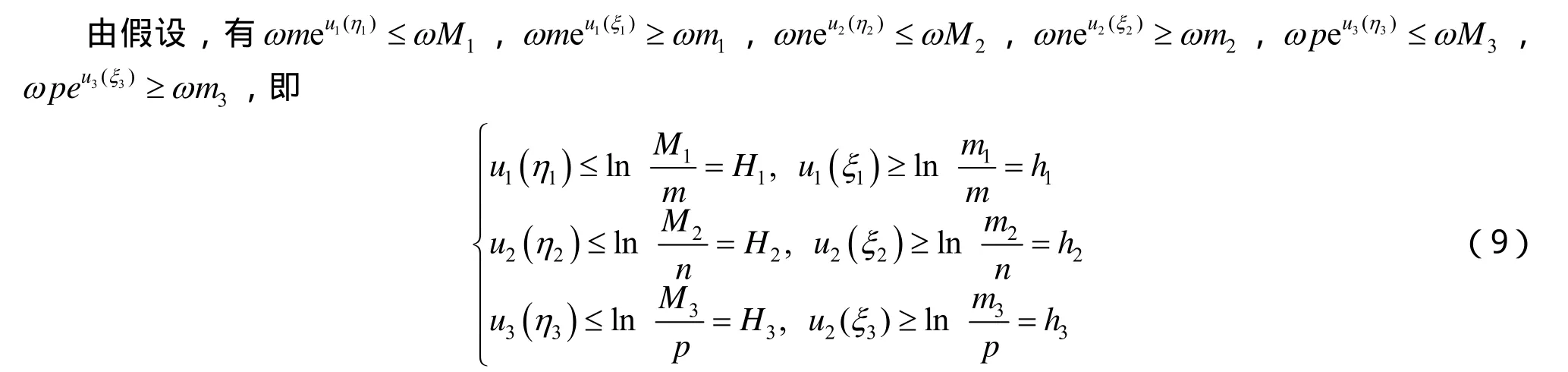
再由式（9）和積分不等式，得

[1] 趙宏偉．帶有多滯量的Lotka-Volterra三種群互惠系統的周期解[J]．吉林大學學報：理學版，2011，49（6）：1034-1038

[2] 趙明，程榮福．一類具生物控制和比率型功能反應的食物鏈系統周期解的存在性[J]．吉林大學學報：理學版，2009，47（4）：730-736

[3] 趙宏偉，王永曦，王銳．具有階段結構和比率依賴的三種群混合模型的周期解[J]．東北師大學報：自然科學版，2009，41（4）：27-31

[4] 王欣欣．具雙密制約和Non-monotonic型功能反應的捕食系統的周期性與全局穩定性[J]．東北師大學報：自然科學版，2009，41（1）：17-22

[5] Yang Fan，Jiang Daqing．Existence of Periodic Solutions of Multidelays Facultative Mutualism System[J]．Chinese Journal of Engineering Mathematics，2002，19（3）：64-68

[6] Chen Fengde，Shi Jinjin，Chen Xiaoxing，et al．Periodicity in Lotka-Volterra Facultative Mutualism System with several delays[J]．Chinese Journal of Engineering Mathematics，2004，21（3）：403-409

[7] 程榮福，常亮．具無限時滯和非單調功能性反應捕食系統的多周期解[J]．吉林大學學報：理學版，2010，48（5）：761-765

[8] Gaines R E，Mawhin J L．Coincidence Degree and Nonlinear Differential Equations[M]．Berlin：Springer-Verlay，1977

Positive periodic solutions of Lotka-Volterra competitive predator prey system with multiple delays

REN Rui-chao，SUN Jie
（Department of Basic Course，Xi'an Modern College of Northwest University，Xi'an 710130，China）

Mawhin's continuation theorem of coincidence degree and integral inequality were used to construct a bounded open sets，and the non autonomous Lotka Volterra predator-prey system of three species with arbitrary time delay was discussed by giving a sufficient condition for the existence of the positive periodic solutions in that if the coefficients satisfied certain conditions，periodic oscillation has been obtained．

Lotka-Volterra competitive system；positive periodic solution；Mawhin coincidence degree theorem

O175.12

A

10.3969/j.issn.1007-9831.2016.06.001

1007-9831（2016）06-0001-05

2016-04-01

2014陜西省教育廳專項科研計劃項目（14JK2146）

任睿超（1985-），男，陜西西安人，講師，碩士，從事微分方程與動力系統研究．E-mail：rrc8512@163.com