譜Galerkin方法的超幾何收斂
陶霞
(湖南理工學院 數學學院,湖南 岳陽 414006)
譜Galerkin方法的超幾何收斂
陶霞
(湖南理工學院 數學學院,湖南 岳陽 414006)
介紹了求解第一類Volterra積分方程的譜Legendre-Galerkin方法和譜Chebyshev-Galerkin方法.數值算例表明,譜Galerkin方法不僅收斂速度快,而且能達到超幾何收斂.
第一類Volterra積分方程;譜Legendre-Galerkin方法;譜Chebyshev-Galerkin方法;超幾何收斂
1 引言及預備知識
許多物理和工程實際問題,如帶記憶性質材料的熱傳導問題,多孔結構粘彈性的壓縮問題和核反應堆中的熱交換過程等,都可以歸結為Volterra積分方程或者Volterra積分微分方程[1-2].積分項的存在,表明這類方程具有物理過程的記憶或反饋性質,這使得它與傳統的微分方程有著本質上的區別.為準確地描述這類物理過程,必須考慮系統對過去經歷的記憶效應.因此,數值計算積分方程不僅存儲量大,而且時間開銷大.如何高效快速且高精度地求解積分方程是一大難點,也是眾多學者迫切希望得以有效解決的難題.
本文主要考慮第一類Volterra積分方程

積分算子定義為

其中:核函數k( x, s)和函數f( x)充分光滑;u( x)為未知函數.通過簡單的線性變換,任意區間上的第一類Volterra積分方程都能轉化成為式(1)的形式.
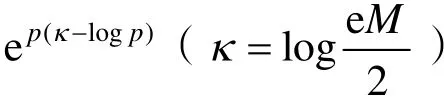
2 譜Galerkin方法

從而得到矩陣形式

3 數值算例
表1 譜Legendre-Galerkin方法的誤差和誤差

表1 譜Legendre-Galerkin方法的誤差和誤差
N 4 6 8 10 12 14 L 誤差 2.38e-1 4.87e-3 5.29e-5 3.55e-7 1.61e-9 1.82e-12 L2誤差 7.00e-2 1.07e-3 9.32e-6 5.20e-8 2.02e-10 2.16e-13
考察譜Chebyshev-Galerkin方法的收斂性質.對于式(3),取為Chebyshev多項式,運用公式(5)計算得到相應的數值解,并計算譜Chebyshev-Galerkin方法的誤差和誤差(見表2和圖2).
表2 譜Chebyshev-Galerkin方法的誤差和誤差

表2 譜Chebyshev-Galerkin方法的誤差和誤差
N 4 6 8 10 12 14 L 誤差 1.87e-1 3.43e-3 3.41e-5 2.12e-7 8.85e-10 2.06e-11 L2 誤差 1.23e-1 1.94e-3 1.71e-5 9.67e-8 3.72e-10 8.37e-12
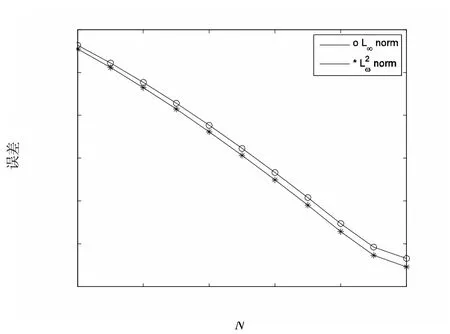
圖2 譜Chebyshev-Galerkin方法誤差圖
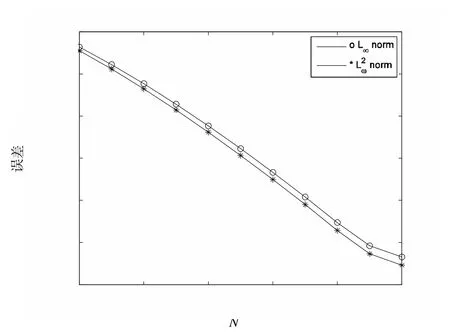
圖1 譜Legendre-Galerkin方法誤差圖
由圖1和圖2可以看出,譜Legendre-Galerkin方法和譜Chebyshev-Galerkin方法同樣具有超幾何收斂性質.
[1] Canuto C,Hussaini M Y,Quarteroni A,et al.Spectral methods:Fundamentals in single domains[M].Newyork:Spring-Verlag,2006:75-90
[2] Shen J,Tang T.Spectral and high-order methods with applications[M].Beijing:Science Press,2006:105-131
[3] Xie Z Q,Li X J,Tang T.Convergence analysis of spectral Galerkin methods for Volterra type integral equations[J].J Sci Comput,2012,53:414-434
[4] Tao X,Xie Z Q,Zhou X J.Spectral Petrov-Galerkin methods for the second kind Volterra type integro-differential equations[J]. Numer Math Theor Meth Appl,2011,4(2):216-236
[5] Zhang Z.Superconvergence of spectral collocation and p-version methods in one dimensional problems[J].Math Comput,2005,74:1621-1636
[6] Zhang Z.Superconvergence of a Chebyshev spectral collocation method[J].J Sci Comput,2008,34:237-246
[7] 李氣發,謝資清,陶霞.譜Legendre-Galerkin方法求解線性積分微分方程的超幾何收斂性分析[J].湖南師范大學自然科學學報,2013,36(2):1-7
[8] Huang Can,Tang Tao,Zhang Zhimin.Supergeometric convergence of spectral collocation methods for weakly singular Volterra and Fredholm integral equations with smooth solutions[J].J Comput Math,2011,29(6):698-719
Supergeometric convergence of spectral Galerkin method
TAO Xia
(School of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,China)
Introduces spectral Legendre-Galerkin method and spectral Chebyshev Galerkin method for solving the first kind Volterra integral equations.Numerical results demonstrate that spectral Galerkin method not only convergent fast,but also has supergeometric convergence.
first kind Volterra integral equations;spectral Legendre-Galerkin method;spectral Chebyshev-Galerkin method;supergeometric convergence
O211.9
A
10.3969/j.issn.1007-9831.2016.06.002
1007-9831(2016)06-0006-03
2016-04-10
國家自然科學基金數學天元基金項目(11426103);湖南省重點學科建設項目;湖南省高校科技創新團隊支持計劃資助項目
陶霞(1982-),女,湖南湘陰人,講師,博士,從事偏微分方程數值解研究.E-mail:xtaohn@163.com

